simmetria

simmetria

La regolarità matematica nella natura e nell’arte

Un fiocco di neve ha un aspetto molto irregolare, eppure, osservato al microscopio, mostra sorprendenti simmetrie. La natura tutta, pur nella varietà che le è propria, presenta molte regolarità di forma, nei visi, nei fiori, nelle strutture degli animali. La simmetria, nel mondo greco, indica la giusta proporzione tra gli elementi e da sempre è collegata alla bellezza. Anche la selezione naturale ha privilegiato la simmetria e in natura ne esistono moltissimi esempi. Ma come riconoscerla? In questo caso la matematica aiuta ad affinare l’occhio

La parola

Il termine simmetria viene dal greco symmetrìa che significa «con misure appropriate». Nel mondo greco antico questa parola indicava l’armonia, le giuste proporzioni tra i diversi elementi di una figura, di un edificio, di un corpo: era dunque un concetto legato alla bellezza (bello) delle forme, anche se basato su precisi riferimenti ai rapporti matematici tra le parti che costituiscono una figura.

Anche oggi la simmetria conserva il suo fascino: la moneta da un euro coniata in Italia riproduce un disegno che Leonardo da Vinci riprese dal trattato L’architettura di Vitruvio. Il concetto di simmetria in questo disegno è associato a quello di giuste proporzioni: il corpo umano viene infatti inscritto in due figure simmetriche, un cerchio (il cui centro coincide con l’ombelico della figura) e un quadrato.

La parola simmetria ha ora un significato matematico più preciso rispetto al passato, anche se essa conserva il suo legame con criteri estetici e di bellezza.

Se ci si riferisce a figure piane, quali quelle che possiamo disegnare su un foglio, occorre distinguere tra due tipi di simmetria molto diversi tra loro: la simmetria rispetto a un centro e la simmetria rispetto a un asse.

Figure simmetriche centralmente

Senza troppo rigore si può dire che una figura è simmetrica rispetto a un centro se, come in un fiocco di neve, la sua forma presenta una certa regolarità attorno a tale punto centrale.

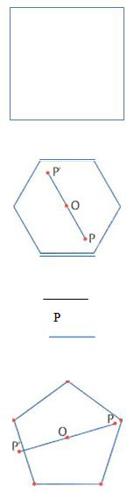
Per essere precisi, però, si deve dire che una figura è simmetrica rispetto a un centro O (centro di simmetria) se per ogni punto P della figura esiste un punto P’ tale che O è a metà tra P e P'’.

Il quadrato e l’esagono regolare costituiscono due esempi di figure simmetriche centralmente e tali sono anche il cerchio e l’ellisse.

fig.

Il pentagono regolare non è invece una figura simmetrica centralmente. Per esempio, il simmetrico del punto P, interno al pentagono, rispetto al centro O cade all’esterno del pentagono. (v. fig.)

Figure simmetriche assialmente

Una figura è simmetrica rispetto a un asse (o simmetrica assialmente) se la sua forma, da una parte e dall’altra di tale asse, è uguale ma ribaltata.

fig.

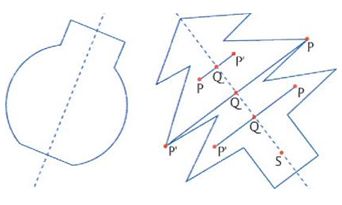
In modo rigoroso, una figura si dice simmetrica rispetto a un asse se esiste una retta r (asse di simmetria) per cui a ogni punto P della figura ne corrisponde un altro P’, ancora appartenente alla figura, dall’altra parte rispetto alla retta e alla stessa distanza da essa. (v. fig.)

La simmetria assiale è detta anche ribaltamento – perché è la trasformazione che si realizza ribaltando una figura lungo un asse –, oppure riflessione – perché l’immagine allo specchio di una figura è la sua simmetrica –. Possiamo verificare, per esempio, che la parola OTTO, scritta in caratteri maiuscoli, è perfettamente simmetrica e posta di fronte a uno specchio rimane uguale a sé stessa.

fig.

fig.

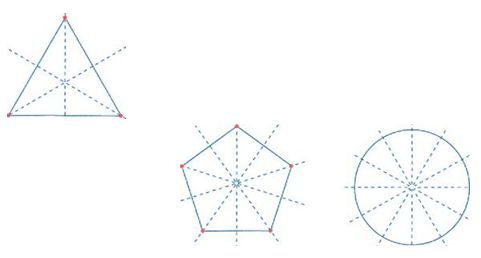
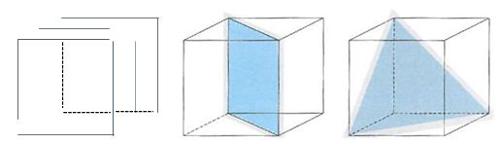
Una figura può essere simmetrica rispetto a più assi: per esempio, il triangolo equilatero ha tre assi di simmetria e il pentagono regolare ne ha cinque (v. fig.). Molti fiori hanno una simmetria simile a quella del pentagono. In modo analogo, molti animali acquatici, come per esempio la stella marina, presentano tale simmetria, detta anche raggiata. La figura simmetrica per eccellenza è il cerchio: esso è infatti simmetrico centralmente e ha infiniti assi di simmetria. Un solido, come per esempio il cubo, può essere simmetrico, oltre che rispetto a un centro o a un asse, anche rispetto a un piano (v. fig.). Quasi tutti gli esseri viventi dotati di movimento autonomo presentano un piano di simmetria e si dicono perciò a simmetria bilaterale.

Simmetrie in natura

Sono diversi i motivi per i quali la selezione naturale ha privilegiato l’evoluzione degli esseri viventi verso forme simmetriche. Alcuni di questi motivi sono legati a un maggior rendimento energetico. Per esempio, consideriamo il caso di certi animali acquatici che non sono dotati di movimento autonomo: la simmetria raggiata o centrale permette loro di restare immobili e ‘catturare’ il cibo in modo indifferente da qualunque parte esso provenga. Invece, gli esseri viventi in grado di spostarsi – compreso l’uomo – presentano una simmetria bilaterale rispetto al piano lungo cui avviene il movimento: ciò permette di raggiungere forme più aerodinamiche e scarti veloci dalla direzione di moto, in caso di fuga o di assalto.

Vi sono poi motivi funzionali che spiegano la simmetria: essa migliora gli organi di senso. Per esempio, i due occhi disposti simmetricamente permettono di valutare le distanze: infatti, anche se non ce ne accorgiamo, gli occhi convergono più o meno a seconda che lo sguardo sia rivolto su un oggetto vicino o lontano. Le due orecchie ai lati della testa, invece, permettono di valutare la direzione da cui proviene un suono: di questo si può fare esperienza diretta quando si ascolta della musica, anche attraverso le cuffie, da un apparecchio stereofonico.

Risparmiare informazioni con le simmetrie

Un motivo della presenza così vasta di simmetrie in natura è da ricercarsi probabilmente anche nel risparmio di informazione genetica. Per ‘costruire’ una figura simmetrica è sufficiente la metà delle informazioni necessarie per costruirne una non simmetrica. Non a caso, se si vuole ritagliare da un foglio di carta una figura simmetrica, basta piegare in due il foglio, sagomare con le forbici una delle due parti e la figura, una volta aperto il foglio, è automaticamente simmetrica.

La simmetria in natura non è mai così perfetta come in geometria. Anzi, talvolta è proprio qualche piccola asimmetria che rende un viso piacevole. Inoltre, alcune asimmetrie sono un potente fattore di evoluzione: saremmo ben diversi se i due emisferi del cervello, apparentemente simmetrici come forma, non svolgessero funzioni sostanzialmente differenti. Uno dei due – generalmente il sinistro, nelle persone che usano di solito la mano destra – prende il comando sull’altro e governa i movimenti fini relativi a una mano e a un piede: quasi tutti perciò prediligono una mano per scrivere e un piede per calciare un pallone. A questo fenomeno si dà il nome di lateralizzazione.

Simmetrie nell’arte

Non c’è tempio, chiesa o cattedrale che, almeno fino all’età contemporanea, non presenti qualche forma di simmetria. Un esempio per tutti è rappresentato dalla facciata di S. Miniato al Monte, a Firenze, risalente all’incirca al 13° secolo.

Anche in musica è frequente il ricorso alla simmetria. Le note sono infatti rappresentate su righi secondo una disposizione geometrica, che corrisponde alla durata e all’altezza dei suoni.

Nell’immagine si vedono due battute di una composizione di Johann Sebastian Bach che formano una figura detta canone a specchio perché la riga superiore è perfettamente simmetrica a quella inferiore rispetto a un asse orizzontale.

Come si disegna una figura simmetrica assialmente

fig.

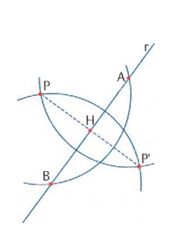
Consideriamo un punto P e una retta r. Il punto P’, simmetrico di P rispetto all’asse r, si determina, utilizzando riga e compasso, in questo modo: con centro in P si apre il compasso di un’apertura qualunque purché l’arco di circonferenza intersechi la retta r in due punti, A e B; con centro in A si traccia un arco di circonferenza di raggio AP; con centro in B si traccia un arco di circonferenza di raggio BP; l’intersezione dei due archi di centri A e B è il punto P’ cercato (v. fig.).

Per disegnare una figura simmetrica rispetto a un asse basta individuare i simmetrici di alcuni suoi punti significativi, quali per esempio i suoi vertici, se la figura in questione è un poligono.

Palindromi

I palindromi sono parole o frasi simmetriche, identiche sia che vengano lette da sinistra a destra sia da destra a sinistra. Alcuni vocaboli palindromi di tre e quattro lettere della lingua italiana sono afa, ala, oro, anna, inni, otto, ma ne esistono anche di più lunghi come: radar, ottetto, ingegni, onorarono. È possibile costruire anche intere frasi palindrome. per esempio amo roma, ai lati d’italia, angela lava la legna, era timida anna ad imitare.