Simulazione

Simulazione

fig. 1

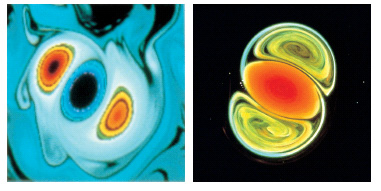
Una delle maggiori innovazioni concettuali della scienza contemporanea, che coinvolge in ugual misura tutte le discipline scientifiche, è la transizione dalla scienza classica, basata sul binomio teoria-esperimento, a una scienza basata sul trinomio teoria-esperimento-simulazione (fig. 1). La s. è una tecnica che permette di ottenere in tempi relativamente brevi informazioni qualitative o quantitative dal modello di un certo fenomeno.

Per estrarre informazioni su un sistema o una situazione, generalmente si individuano alcune proprietà ritenute essenziali e si ricompongono producendo quello che si definisce un modello della realtà in esame (v. modellistica matematica, in questa Appendice). Un modello quindi è un simulacro di realtà che ha alcuni vantaggi: essere più facilmente riproducibile e controllabile; rendere più agevole l'estrazione di informazioni; rendere più agevole la costruzione di scenari ipotetici, intervenendo sui parametri ed estraendo l'informazione sulle conseguenze.

Per simulazione, in senso lato, si intende la descrizione del comportamento del modello. Tutte le informazioni necessarie per tale descrizione sono implicitamente contenute nel modello stesso, ma il renderle esplicite in un ambiente controllato e misurabile è spesso un compito insolubile per chiunque, e non per incapacità individuali, ma per l'intrinseca complessità del problema. Si può affermare che la s. sia, in qualche misura, un esperimento virtuale: è un esperimento poiché in essa si tenta di osservare eventuali differenze qualitative nel comportamento di un sistema in corrispondenza alla variazione di certi parametri, ed è virtuale poiché il sistema che si osserva non è un reale sistema fisico, ma un suo simulacro.

Le tecniche di s. hanno ricevuto negli ultimi tempi un impulso notevole per la varietà di contesti in cui esse sono applicate, grazie all'aumento continuo di potenza nei sistemi di elaborazione dell'informazione e alla corrispondente diminuzione dei costi che consentono di gestire modelli sempre più dettagliati e complessi. Oggi gran parte delle attività sperimentali nelle scienze, delle attività di progettazione nell'ingegneria, delle attività di valutazione delle prestazioni o di studio dell'evoluzione nei sistemi complessi artificiali o naturali, sono svolte con l'ausilio della s., sollevando rilevanti problemi di rispondenza tra i comportamenti simulati e quelli effettivi. La consapevolezza di tali problemi è una componente essenziale della cultura contemporanea dato che la s. è uno strumento che sta assumendo un ruolo crescente in particolare nei processi decisionali a tutti i livelli. Il rischio di sopravvalutarne il potere previsionale o normativo può avere conseguenze anche catastrofiche.

Simulazione e modelli logico-matematici

Esistono diversi tipi di modelli che corrispondono quindi a diversi tipi di s. in cui sono presenti sia componenti fisiche, sia modelli astratti implementati su un elaboratore, sia modelli concettuali realizzati su supporti grafici di vario tipo:

a) modelli fisici in scala del sistema in esame (per es., modelli di navi in vasche artificiali per analizzare il comportamento idrodinamico; modelli di robot per verificarne le funzionalità; modelli di strutture per verificarne le deformazioni sotto sforzo e i carichi di rottura; modelli in scala ridotta di edifici per valutare aspetti estetici o funzionali; tunnel del vento ecc.);

b) modelli che riproducono situazioni ambientali (per es., simulatori di volo per l'addestramento dei piloti; business game, ovvero giochi di decisione relativi alla conduzione di imprese; esercitazioni antincendio, antiterremoto o abbandono nave, s. di incidenti nelle centrali nucleari);

c) modelli qualitativi per verificare gli effetti di scelte di vario tipo (per es., ipotesi di business, politiche di mercato, strategie politiche);

d) modelli logico-matematici per lo studio quantitativo delle relazioni tra grandezze osservabili sulla base di un modello.

In realtà, tutte le scienze studiano relazioni tra grandezze osservabili in sistemi che possono essere fisici, chimici, economici, tecnici, organizzativi, sociali, di produzione, di servizio ecc. Il primo livello di conoscenza di tali relazioni è quello qualitativo, che stabilisce una connessione tra la variazione di una grandezza e quella di un'altra. Un secondo, più preciso, livello è quello quantitativo in cui si cerca di definire quanto, al variare di una grandezza, vari un'altra. Tale livello è basato sulla costruzione di modelli matematici. Qui di seguito verrà trattata solo quest'ultima forma di simulazione.

I modelli matematici classici hanno avuto i loro maggiori successi nei casi in cui era possibile isolare un piccolo numero di grandezze osservabili e giustificare l'ipotesi che l'influenza di tutte le rimanenti osservabili su quelle selezionate fosse trascurabile. Nei casi in cui l'evoluzione di una grandezza osservabile dipenda invece da moltissimi fattori, per tenere conto di essi e non discostarsi completamente dalla realtà, un modello matematico conduce a equazioni la cui soluzione esplicita è possibile solo in rarissimi casi. Si pone quindi il problema di come estrarre informazioni da un modello di cui non si conosce la soluzione (o le soluzioni).

La matematica ha sviluppato due tipi di tecniche per affrontare questo problema, le tecniche di approssimazione e l'analisi qualitativa, che hanno funzionato molto bene per una vasta classe di fenomeni fisici. Anche in fisica i problemi esplicitamente risolubili sono un'eccezione, ma una buona parte dell'arte del fisico consiste nell'elaborare ragionevoli approssimazioni nella fase di definizione delle equazioni fondamentali e nel trarre da queste conseguenze d'interesse fisico. Tuttavia, nessuna di queste due tecniche è applicabile ai sistemi complessi, in cui non solo le variazioni di una grandezza dipendono da molti fattori, ma in tale dipendenza tutti questi fattori intervengono in modo essenziale (v. complessità: Sistemi complessi, in questa Appendice). Si può dire che tali variazioni sono effetto di un fenomeno collettivo, cosicché non è possibile, neppure in modo idealizzato e approssimativo, distinguere naturalmente tra questi fattori una classe che svolge un ruolo essenziale da un'altra i cui effetti possano considerarsi come piccole perturbazioni di quelli dovuti ai primi. D'altra parte, l'analisi qualitativa condotta con gli strumenti classici della matematica porta spesso a conclusioni molto lontane da quelle che possono essere interessanti a fini applicativi (tipicamente teoremi di esistenza, unicità o non unicità per le soluzioni, o informazioni molto generali e qualitative su di esse).

Un approccio alternativo è quello della s. per modelli logico-matematici. Tale approccio avviene secondo due schemi fondamentali: uno analitico o per equazioni, l'altro a rete o per prescrizioni locali.

Nello schema analitico, o per equazioni, si parte da un insieme di equazioni che, sulla base di esperienze precedenti, si suppone descriva abbastanza bene la situazione che interessa, e si cerca di estrarre informazioni da questo. Per es., nessuna galleria del vento esistente potrebbe riprodurre le condizioni incontrate dalle navette spaziali al rientro nell'atmosfera terrestre; di conseguenza, per avere informazioni sulle pressioni e temperature che il veicolo dovrà sopportare e su come queste si distribuiranno sulle sue diverse zone, si simulano al calcolatore tali condizioni utilizzando le equazioni dell'idrodinamica e della termodinamica classica (solo un computer molto potente è in grado di gestire l'immensa mole d'informazioni da elaborare per arrivare a un risultato). In modo analogo viene studiata la combustione all'interno dei motori e si elaborano le previsioni meteorologiche.

A

B

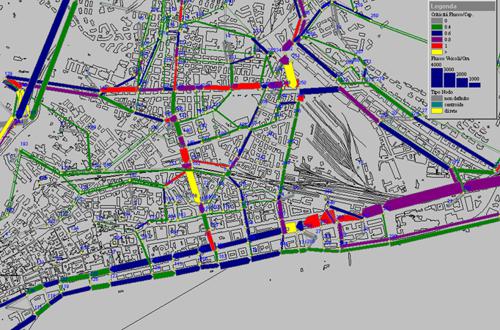
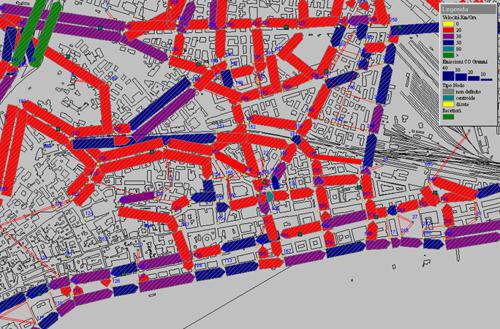
Nello schema a rete, o per prescrizioni locali, si parte da un insieme di componenti elementari, caratterizzati da una molteplicità di possibili stati, e di regole di decisione predefinite che determinano l'evoluzione dello stato delle singole componenti in funzione dell'interazione con le altre (come algoritmi genetici, reti neurali, reti di Petri o reti di code). Casi tipici di sistemi a rete sono: i flussi di parti in una fabbrica, i flussi di informazione in un sistema di elaborazione, i flussi di veicoli in un sistema di trasporti (fig. 3 A e B), i flussi di messaggi in una rete di telecomunicazioni, la diffusione di un'epidemia o le sollecitazioni di piattaforme oceaniche sotto l'effetto del vento e del mare. In questi casi le regole di comportamento dei singoli sistemi vengono rappresentate in modo semplice e la complessità globale del comportamento della rete nasce dalla molteplicità dei suoi elementi e delle loro interazioni: l'evoluzione del sistema non viene descritta globalmente attraverso un sistema di equazioni, ma attraverso un insieme di prescrizioni locali per l'aggiornamento dello stato delle singole componenti.

Spesso il modello matematico non è noto sin dall'inizio e quindi occorre procedere in modo induttivo invece che puramente deduttivo, tentando di impostarne uno attraverso una serie di approssimazioni successive. Si ipotizzano uno o più modelli iniziali semplificati, si estraggono da essi, tramite la s., delle conseguenze qualitative, si paragonano tali conseguenze con dati reali, e si usa iterativamente tale paragone per correggere, arricchire o integrare i singoli modelli. Per passi successivi si può arrivare a modelli complessivi di grandi dimensioni, difficili da trattare e di cui può essere difficile valutare la rispondenza alla realtà.

In molti modelli logico-matematici un sistema viene descritto attraverso il suo spazio delle configurazioni e la sua complessità è misurata sia dall'altissimo numero di dimensioni di tale spazio, sia dal tipo di interazione tra le varie configurazioni. Tale interazione è descritta da una funzione (interpretata come energia o costo della configurazione) e il problema consiste nel cercare le configurazioni che rendono minima la funzione costo. L'interesse di tali modelli sta nel fatto che, pur nella loro semplicità strutturale (per definirli basta definire lo spazio delle configurazioni e assegnare la funzione d'interazione), essi riescono a descrivere una grande varietà di situazioni. Estrarre informazioni da questi modelli equivale, in molti casi, a studiare il seguente problema matematico: dato un insieme finito di punti e una funzione definita su di essi, trovare il massimo (o il minimo) di questa funzione. La difficoltà di risoluzione di questo problema (generalmente indicata come complessità computazionale, v. informatica: Scienze dell'informazione e complessità: Sistemi complessi, in questa Appendice) è strettamente collegata con la difficoltà di rappresentare e simulare il funzionamento di un sistema complesso.

L'introduzione della s. nello studio dei sistemi deterministici ha cambiato profondamente il contesto in cui operano scienziati, ingegneri e tecnici in quanto introduce elementi di realtà virtuale. Nel 1970 M. Krufer ha coniato questa espressione con riferimento a elementi sensoriali riprodotti artificialmente. Tuttavia, il suo significato odierno va molto oltre i primi esempi. Infatti, ogni operazione compiuta non sulla base della realtà, bensì di una sua rappresentazione astratta (generalmente attraverso un supporto informatico), e che comporta non un'azione effettiva, ma il semplice inserimento di dati in un opportuno sistema, può essere vista come eseguita in un contesto virtuale, in cui il problema della corrispondenza con la realtà è spostato a un livello superiore di controllo e gestione delle operazioni.

Un esempio di studio svolto sulla base di modelli, in un contesto virtuale, è quello della dinamica molecolare, importante tecnica computazionale nello studio dello stato fluido e solido della materia. In essa le forze intermolecolari sono esplicitamente calcolate e i moti delle molecole integrati, usando le equazioni del moto di Newton e utilizzando vari tipi di approssimazioni per il potenziale intermolecolare. La dinamica molecolare si può confrontare con il tentativo di fare le previsioni del tempo risolvendo le equazioni di Navier-Stokes della dinamica dei fluidi. Occorrerebbe dimostrare che una previsione deterministica basata sulla soluzione delle equazioni di Navier-Stokes, quando si tenga conto dell'approssimazione dei dati iniziali, degli errori di arrotondamento, degli errori di discretizzazione, è più affidabile di una previsione statistica. Ma, in effetti, l'esperienza in molti casi sembra mostrare esattamente l'opposto.

Molti sistemi per cui è rilevante l'uso della s. sono caratterizzati da grandezze di cui è possibile prevedere il valore solo in modo approssimato, in cui cioè, per mancanza di informazione o per intrinseca variabilità dell'ambiente o di alcuni componenti, l'evoluzione del sistema è descrivibile solo attraverso grandezze definite su base probabilistica. Per tali sistemi, detti casuali, vi sono essenzialmente due metodi di base per la s.: i metodi Monte Carlo (v. App. V) che, a partire da esperimenti numerici su grandezze aleatorie, sono sempre in grado di generare una risposta al problema, ma che, al più, garantiscono che tale risposta sia esatta con una data probabilità p (nei casi più fortunati tale probabilità può essere resa arbitrariamente vicina a 1); e i metodi Las Vegas, che, al contrario, possono ammettere una risposta al problema di cui non sempre è possibile valutare a priori la probabilità, ma che, se la producono, è certamente esatta.

Per chiarire la differenza tra i due metodi consideriamo alcuni esempi. Supponiamo che, dato un numero intero positivo x, si voglia stabilire se esso ha o no la proprietà P (per esempio la proprietà di essere un numero primo). Supponiamo inoltre di conoscere, dalla teoria dei numeri, una funzione Q di due variabili con la seguente proprietà: se trovo un intero y tale che Q(x, y) è minore di zero, allora certamente x ha la proprietà P (ma, se Q(x, y) è maggiore di zero, non è detto che x abbia tale proprietà). In questo caso, una possibile strategia per provare che x ha la proprietà P è la seguente: scelgo a caso dei numeri y e calcolo il valore di y tale che Q(x, y) sia minore di zero; posso allora concludere con certezza che x ha la proprietà P. Se però non trovo un tale y, allora non posso concludere niente e non ho risolto il problema. Questo è un algoritmo Las Vegas.

Un esempio di algoritmo Monte Carlo è invece il seguente: è data una regione A contenuta in un quadrato e si vuole calcolarne la superficie. Se genero a caso (cioè con distribuzione uniforme) dei punti nel quadrato, allora la probabilità che un punto cada nella regione A è proporzionale alla superficie di A. Per la legge dei grandi numeri, la probabilità che, in un gran numero di prove indipendenti, la frequenza relativa dei punti caduti in A si discosti di molto dalla probabilità di cadere in A è piccolissima. Pertanto, se in un gran numero di punti generati a caso, circa i due terzi cadono nella regione A posso concludere che con alta probabilità la superficie di A è circa i due terzi di quella del quadrato.

Alla base di ogni s. di sistemi casuali vi è la generazione di sequenze di numeri casuali. Simulare il caso significa insegnare a un calcolatore a produrre sequenze casuali. Ciò non è in realtà possibile poiché sarebbe una contraddizione in termini. Quello che si può fare è insegnare a un calcolatore a imitare le sequenze casuali. I risultati di queste imitazioni vengono chiamati sequenze pseudocasuali.

Eventi completamente casuali sono ovviamente impossibili da prevedere: si può dire che un eventuale algoritmo di previsione avrebbe una complessità infinita. Esistono però anche semplici sistemi completamente deterministici i cui comportamenti risultano difficili da descrivere con precisione. È ben noto infatti che anche sistemi non lineari di piccole dimensioni possono avere comportamenti caotici. Tali comportamenti, in mancanza di informazioni sul modello, vengono a volte anche descritti su base probabilistica.

Le tecniche della simulazione con l'elaboratore

La s. con l'elaboratore si basa, da una parte, su un modello concettuale, tipicamente con una struttura a rete, del sistema che si vuole analizzare o di alcune sue parti e dei processi di decisione che avvengono localmente nei suoi singoli elementi e, dall'altra, su un insieme di strumenti e tecniche, spesso di tipo statistico, i quali permettono di simulare l'evoluzione complessiva del sistema a partire da un insieme di relazioni logico-matematiche che modellano le funzioni dei diversi sottosistemi e componenti elementari e da un insieme di regole di decisione predefinite, che permettono di risolvere eventuali problemi di scelta.

Naturalmente anche la modellistica del singolo elemento, al fine di descriverne adeguatamente il comportamento, può costituire un aspetto rilevante di una simulazione. Questa, tuttavia, è spesso un'attività meno strutturata, fortemente dipendente dal contesto cui l'elemento appartiene e dalle capacità dell'analista. Vi è, invece, una più ampia letteratura e disponibilità di supporti normativi e metodologici relativa alle attività di integrazione di diversi elementi in un sistema complessivo.

La gestione della configurazione di un sistema complesso, l'analisi strutturata di organizzazioni e processi decisionali, molte prescrizioni della qualità totale, molti strumenti di rappresentazione e analisi di sistemi a rete, le tecniche di scomposizione strutturata e di integrazione di attività, le tecniche di gestione progetti e di ingegneria concorrente, sono solo alcuni strumenti sviluppati in ambito prevalentemente aziendale per far fronte alle esigenze di integrazione.

Un aspetto comune a queste tecniche riguarda l'attenzione dedicata ai meccanismi di interazione fra elementi, e, in particolare, alle modalità con cui si sviluppano i flussi di informazione e il processo decisionale in un sistema a rete. Per rendere più efficace la s. vengono utilizzati strumenti (spesso sviluppati ad hoc) per la grafica interattiva, la visualizzazione dei risultati, la costruzione modulare di parti del simulatore, l'analisi dei risultati. I moderni ambienti per la programmazione orientata a oggetti, per la rapidità di programmazione e la semplicità di uso, offrono un potente supporto allo sviluppo della simulazione. In casi particolari, in cui la potenza di calcolo richiesta è molto elevata, si ricorre all'uso di strumenti di elaborazione parallela, con lo sviluppo di sistemi di elevata complessità per la gestione della s. concorrente.

In pratica i sistemi da analizzare contengono spesso grandezze definite su base probabilistica; in questo caso i modelli di s. richiedono l'introduzione di procedure per la generazione di numeri casuali e di valori descritti da opportune distribuzioni di probabilità; i modelli di s. stocastici sono generalmente più complessi, più costosi e con un comportamento meno prevedibile di quelli deterministici. Inoltre essi richiedono, in genere, tempi di elaborazione più lunghi per ottenere una stima affidabile della distribuzione di probabilità delle grandezze sotto osservazione, cosa particolarmente critica quando tali grandezze si riferiscono a eventi rilevanti, ma di bassa probabilità (per es. nella valutazione della probabilità di incidente in una centrale nucleare).

Le fasi principali del processo di costruzione di un simulatore, simili a quelle di costruzione di un qualsiasi modello, sono tipicamente:

a) definizione qualitativa del problema;

b) formulazione degli obiettivi della s.; individuazione delle grandezze significative del sistema da simulare e loro suddivisione in due classi, dati e grandezze controllabili; scelta del livello di aggregazione (cioè del livello di dettaglio della descrizione), valutazione delle dimensioni, dei tempi e dei costi, valutazione delle diverse architetture utilizzabili;

c) scelta dell'ambiente hardware e software (elaboratore, software esistente, da sviluppare o da acquisire per le varie fasi, scelta del linguaggio di programmazione);

d) formulazione del modello (schema a blocchi o definizione dei componenti elementari della rete, specifiche e caratteristiche funzionali dei singoli componenti elementari e delle relazioni fra essi);

e) predisposizione dei dati (identificazione dei dati necessari, raccolta dati, organizzazione dei dati in strutture idonee all'elaborazione); implementazione del modello (architettura del simulatore, sviluppo del software, integrazione del software, fusione dei dati); progetto degli esperimenti (predisposizione di un insieme di esperimenti adeguati a fornire l'informazione cercata, definizione delle eventuali elaborazioni dei risultati della simulazione);

f) esecuzione degli esperimenti (in condizioni nominali, analisi di sensibilità o parametriche rispetto a variazioni di dati e/o di struttura); analisi e interpretazione dei risultati (analisi statistica, analisi sulla base di informazioni esterne, valutazione del significato operativo); validazione (definizione delle modalità di verifica e certificazione, valutazione dell'attendibilità dei risultati, della robustezza del modello, della facilità di uso e di modifica);

g) documentazione (del simulatore, del processo di costruzione, degli input utilizzati, degli esperimenti fatti, dei risultati, dell'uso del simulatore o di sue parti) e gestione (del simulatore durante tutto il suo ciclo di vita, modifiche di configurazione e validazione di nuove configurazioni).

Un problema che si pone nella costruzione di un simulatore riguarda il modo con cui cambia, nel simulatore, il tempo relativo all'evoluzione del sistema simulato. In effetti, quando si effettuano esperimenti di s. si ha a che fare con l'evoluzione di due tempi diversi: uno è il tempo reale, misurato da un cronometro esterno alla s., per es. l'orologio al polso dello sperimentatore; l'altro è il tempo relativo all'oggetto simulato, misurato da un contatore interno alla simulazione. Questi due tempi sono generalmente molto diversi. Spesso in pochi minuti vengono simulati giorni di funzionamento di un sistema reale (simulazione in tempo accelerato). In altri casi, per limitazioni nella potenza di calcolo, sono necessarie ore di s. per ricostruire interazioni fra particelle subatomiche di milionesimi di secondo (simulazione in tempo ritardato). In alcuni casi, si desidera che i due tempi siano uguali; questo è il caso, per es., dei simulatori di volo, in cui il simulatore deve presentare all'operatore la situazione come si evolverebbe nella realtà (simulazione in tempo reale).

Per gestire il tempo all'interno del simulatore, vi sono due approcci tipici, che vengono detti: simulazione sincrona e simulazione asincrona o a eventi. Con la s. sincrona il tempo avanza nel simulatore per passi di una fissata quantità Δt, scelta come unità di tempo elementare; le grandezze presenti nel simulatore vengono aggiornate ogni Δt unità di tempo e, se Δt è sufficientemente piccolo, può essere buona l'approssimazione ottenuta e bassa la probabilità che si verifichino eventi, rilevanti ai fini dei risultati, mascherati dall'intervallo scelto. Con la s. asincrona, più diffusa e per la quale sono disponibili molti supporti software, il tempo avanza nel simulatore di una quantità variabile, che dipende dal verificarsi degli eventi significativi; a ogni istante in cui si trova il simulatore, viene calcolato l'istante del primo evento significativo successivo e il simulatore sposta il tempo corrente in tale istante, compiendo gli opportuni aggiornamenti delle variabili, seguendo un calendario degli eventi significativi costruito durante l'esecuzione e non noto a priori.

Campi d'impiego della simulazione

Mediante la s., l'utente può ottenere indirettamente risposta ad alcuni problemi decisionali o di comportamento, in modo più rapido, più economico e con meno rischi che non operando sul sistema reale, e questo strumento acquista ancora maggiore importanza nei casi in cui non è possibile effettuare esperimenti su tale sistema. Infatti, egli può provare sul sistema simulato diverse strategie decisionali, regole di decisione, condizioni ambientali, eventi anomali, e valutare i conseguenti comportamenti del sistema e, in particolare, le sue prestazioni. Infine, benché la s. venga generalmente utilizzata in campo tecnico-scientifico per analizzare la dinamica di un sistema, sono molte le applicazioni significative per problemi di tipo statico, quali, per es., quelli di determinazione di condizioni di equilibrio.

In economia viene diffusamente impiegata per prevedere le conseguenze di interventi di vario tipo (per es. la definizione del tasso di sconto o l'individuazione degli interventi sulle monete per ottenere i tassi di cambio desiderati) o il comportamento di agenti operanti sul mercato (competitori o alleati), con tecniche spesso mutuate dall'intelligenza artificiale e dalla teoria dei giochi.

Nelle scienze biomediche viene utilizzata per studiare l'effetto di farmaci, per mettere a punto protocolli di cura, per studiare la risposta del sistema immunitario, per studiare il comportamento di aggregati complessi (come, per es., sistemi ecologici e ambientali) al variare delle condizioni esterne.

Nelle reti di servizio (in particolare, nei sistemi di trasporto e di telecomunicazione) viene impiegata, spesso integrata da strumenti di ottimizzazione, sia per la progettazione della rete, sia per la gestione dei flussi di traffico.

Nell'ingegneria industriale la s. si presta alla determinazione sia delle scelte strategiche (in particolare, la scelta di prodotto e di processo), sia delle scelte tattiche (come la scelta di procedure o la gestione progetti), sia delle scelte operative (come la scelta dell'ordine con cui effettuare le operazioni di montaggio, gli interventi a fronte dei flussi reattivi laminari e turbolenti nella combustione, la verifica di correttezza nella progettazione software, la programmazione di robot di lavorazione).

Nelle regate veliche e nelle gare automobilistiche, la s. può operare per il confronto tra diverse rotte e la determinazione delle strategie di gara.

Nel controllo a distanza di apparati, veicoli e impianti, viene utilizzata per sostenere strumenti di riproduzione virtuale della realtà, con risultati spesso simili a quelli ottenuti da alcuni videogiochi.

Nella formazione e addestramento, infine, viene utilizzata per consentire agli operatori di familiarizzare in tempi rapidi con sistemi complessi, formati da un gran numero di parti e per guidarli nelle procedure di intervento.

bibliografia

K.D. Tocher, The art of simulation, London 1963.

H. Kobayashi, Modeling and analysis. An introduction to system performance evaluation methodology, Reading (Mass.) 1966.

G.A. Mihram, Simulation: statistical foundation and methodology, New York 1972.

G.S. Fishman, Principles of discrete event simulation, New York 1978.

B. Khoshnevis, Discrete systems simulation, New York 1994.

A.M. Law, W.D. Kelton, Simulation modeling and analysis, New York 1996.

R.Y. Rubinstein, B. Melamedi, Modern simulation and modeling, New York 1998.