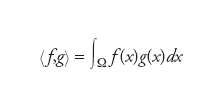spazio di Hilbert
spazio di Hilbert
Per poter enunciare il teorema di Pitagora nel piano, occorre definire quando due vettori sono tra loro ortogonali; ciò si ottiene dalla nozione di prodotto scalare di due vettori, che associa a due vettori un numero reale (questo numero è zero se i due vettori sono ortogonali). Uno spazio di Hilbert ℋ è uno spazio di Banach che generalizza il normale piano euclideo, ossia su cui è definito un prodotto scalare. Si tratta di una funzione 〈∙,∙〉 da ℋ×ℋ in ℝ, con queste proprietà: (a) 〈∙,∙〉 è lineare in entrambe le variabili; (b) è simmetrica, cioè 〈a,b〉=〈b,a〉; (c) 〈a,a〉≥0 e 〈a,a〉=0 se e solo se a=0. Lo spazio si intende normato dalla norma ∥a∥=√〈a, a〉. Per es., lo spazio L2(Ω) delle classi di equivalenza delle funzioni a quadrato sommabile è uno spazio di Hilbert con il prodotto scalare