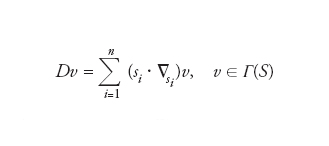struttura di spin
struttura di spin
Un fibrato principale π∼:P∼→M su una varietà n-dimensionale M con gruppo di struttura Spinn che sia ottenuto come ricoprimento di un qualche fibrato principale π :P →M con gruppo di struttura SOn, la componente connessa all’identità del gruppo ortogonale. Questo significa che esiste un omomorfismo suriettivo φ:P∼→P di fibrati principali uguale all’identità sulla base M e compatibile con l’omomorfismo naturale ϱ:Spinn→SOn. Ricordiamo che Spinn è proprio il (doppio) ricoprimento del gruppo SOn e ammette una rappresentazione su uno spazio vettoriale S di dimensione 2r, con n=2r se n è pari e n=2r+1 se è dispari. Gli elementi dello spazio S sono detti spinori. Il caso più importante è quello di una varietà di Riemann M con metrica g: il fibrato principale π:P→M è ottenuto considerando l’azione di SOn su T*(M), il duale del fibrato tangente T(M) alla varietà M ossia lo spazio dei campi (regolari) di forme lineari sui campi vettoriali (regolari) di M. Similmente, si possono definire strutture di spin su varietà semi-riemanniane come per es. la varietà che descrive lo spazio-tempo della relatività generale o ristretta. Condizioni necessarie e sufficienti per l’esistenza di una struttura di spin su una varietà M sono l’orientabilità di M e l’annullarsi della classe di Stiefel-Withney W2(M). Ogni struttura di spin π∼, su una varietà riemanniana M individua un fibrato vettoriale πS:S(M)→M con fibra tipica S, detto fibrato di spinori, e su di esso la connessione di Riemann di M determina canonicamente una connessione. L’importanza del fibrato πS:S(M)→M risiede nel fatto che sullo spazio Γ(S) delle sue sezioni (campi spinoriali su M) agisce l’operatore di Dirac D, definito dalla
dove ∇si (i=1,...,n) sono le derivate covarianti nella direzione dei campi di vettori ortonormali si . L’operatore di Dirac è l’oggetto del teorema dell’indice di Atiya-Singer nella sua forma più generale.