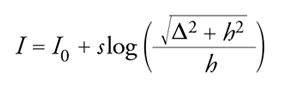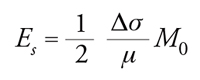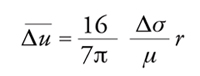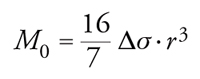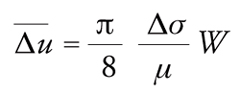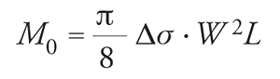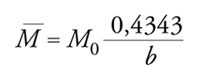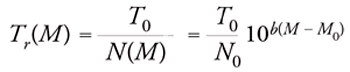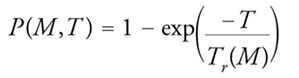Terremoti. Aspetti generali
Terremoti. Aspetti generali
Il termine terremoto è usato sia nel suo significato letterale di movimento del suolo prodotto sulla superficie terrestre da cause a essa interne, sia con riferimento al processo di liberazione dell'energia elastica da cui tali movimenti sono originati, accomunando così, con una sola parola, sia le cause sia gli effetti di questo fenomeno naturale. Pertanto si parla correntemente di terremoti sussultori od ondulatori, ma anche di terremoti superficiali, profondi, e così via. Come per altri campi delle scienze naturali, lo studio dei terremoti è stimolato non soltanto dal desiderio di aumentare le nostre conoscenze sulle leggi che governano l'ambiente in cui viviamo, ma anche dall'uso pratico che si potrà fare di queste conoscenze per mitigare i danni provocati dai terremoti sulle persone e sulle loro proprietà.
È tradizionalmente ritenuto che i terremoti possano avere origine tettonica, vulcanica o da crollo. Tuttavia le conoscenze moderne hanno permesso di stabilire che i terremoti di origine vulcanica (ossia prodotti da spostamento di fluidi negli apparati vulcanici, da non confondere con i terremoti tettonici in zona vulcanica) sono dal punto di vista energetico una quantità minima rispetto a quelli tettonici, e quelli causati da crollo ne rappresentano addirittura una frazione trascurabile. Inoltre solo i terremoti di origine tettonica non sono caratterizzati da effetti esclusivamente locali. Per terremoti tettonici si intendono quelli prodotti da fratture di parti rigide della crosta terrestre o della litosfera, la cui estensione può variare da alcuni metri, nel caso di terremoti di interesse esclusivamente scientifico, a oltre un migliaio di chilometri, per i più importanti terremoti mai avvenuti. Queste fratture possono essere immaginate come veri e propri strappi, a loro volta causati dalle deformazioni elastiche accumulate nel tempo dallo spostamento lento, ma costante, delle placche litosferiche l'una rispetto all'altra.
Quasi tutti i grandi terremoti traggono origine dal moto delle placche e dalla loro interazione reciproca, quindi l'energia liberata dai terremoti deve essere fornita dalle forze di spostamento delle zolle litosferiche. Tale energia motrice è individuata nei moti convettivi della parte calda e plastica della Terra, chiamata astenosfera, per effetto del riscaldamento prodotto dal decadimento degli elementi radioattivi. Le superfici di distacco sulle quali si muovono i vari blocchi di crosta terrestre, dette faglie, possono essere visibili in circostanze particolari anche in superficie e se ne può stimare direttamente la velocità di dislocazione media, che nei casi più eclatanti si avvicina a decine di centimetri l'anno.
sommario
1. Origine dei terremoti. 2. Localizzazione dei terremoti. 3. Intensità dei terremoti. 4. Magnitudo. 5. Modelli meccanici dei terremoti. 6. Statistica dei terremoti. 7. Pericolosità sismica e prevedibilità a lungo termine dei grandi terremoti. 8. Precursori e prevedibilità a breve termine dei terremoti. 9. Mitigazione del rischio sismico. □ Bibliografia.
Origine dei terremoti
Si innesca una rottura che si propaga rapidamente lungo una superficie, detta piano di faglia, quando in un punto si raggiunge un livello di deformazione incompatibile con la resistenza del materiale. Il tempo necessario ad accumulare uno sforzo sufficiente a causare la frattura del mezzo elastico costituito da rocce cristalline (sforzo che si valuta essere dell'ordine di 50 MPa per la roccia intatta) è compreso tra poche decine di anni e molti millenni, a seconda della velocità di deformazione e della resistenza delle rocce in questione.
I terremoti tendono ad avvenire in corrispondenza di faglie già messe in movimento da eventi precedenti. A seconda dell'inclinazione del piano di faglia rispetto al piano orizzontale e della direzione del movimento di dislocazione sul piano di faglia stesso, i terremoti sono schematicamente classificati come terremoti a meccanismo normale, inverso e trascorrente. I primi si collegano a fratture che avvengono come risposta a una deformazione di tipo estensionale orizzontale, i secondi sono causati da deformazioni di tipo compressivo orizzontale, quelli a meccanismo trascorrente da una deformazione orizzontale di taglio. I meccanismi dei terremoti raramente sono ascrivibili esattamente a uno soltanto di questi tipi, ma più comunemente rappresentano casi intermedi fra uno dei primi due e il terzo.
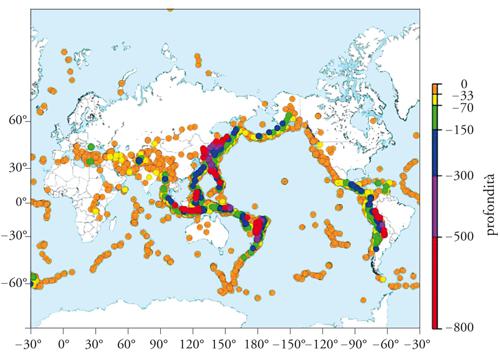
La distribuzione geografica dei terremoti sul globo terrestre (fig. 2) mostra chiaramente che le sorgenti sismiche sono tendenzialmente allineate su fasce larghe poche decine di chilometri e lunghe varie migliaia di chilometri; grandi aree oceaniche e continentali sono quasi inattive. Più del 90% dell'energia sismica liberata nella Terra proviene dalla fascia circumpacifica, una lunga catena di fratture che consentono lo scorrimento delle placche oceaniche sotto quelle continentali lungo le zone di subduzione. In queste zone le sorgenti sismiche tendono a divenire sempre più profonde dall'oceano verso l'interno dei continenti formando delle superfici inclinate dette piani di Benioff, che giungono fino ad alcune centinaia di chilometri di profondità. Notevole è anche l'attività sismica delle catene mediane degli oceani (Atlantico, Indiano, Pacifico, Artico e Antartico) dove le placche oceaniche subiscono un processo di deformazione distensiva accompagnato dalla formazione di attività vulcanica. Esistono poi zone sismiche attive originate dalla compressione fra due placche continentali (come avviene nell'Himalaya), o per scorrimento orizzontale di taglio (di cui due esempi sono la faglia di San Andreas in California e la faglia Nord-Anatolica).
Nell'Italia peninsulare, la maggior parte della sismicità è causata dallo stato di tensione orizzontale dell'Appennino in direzione sud-ovest nord-est ed è quindi caratterizzata da terremoti a meccanismo normale in direzione appenninica, o trascorrente in direzione antiappenninica. Nell'Italia nord-occidentale, invece, si riscontrano più comunemente terremoti a meccanismo inverso (dovuti a uno stato di sforzo compressivo).
Localizzazione dei terremoti
Il modello più semplice per la sorgente di un terremoto è quello puntiforme. Anche se fisicamente poco realistico (l'energia che si libera sotto forma di onde elastiche non può scaturire da un unico punto) tale modello presenta vantaggi pratici che ne giustificano ancora l'uso. Nel modello puntiforme la sorgente del terremoto è definita ipocentro, il punto della superficie terrestre sulla sua verticale è chiamato epicentro e la distanza fra ipocentro ed epicentro è denominata profondità ipocentrale.
La localizzazione macrosismica dell'epicentro di un terremoto si effettua individuando il luogo dove i suoi effetti si sono risentiti con la maggiore intensità. Questo tipo di localizzazione era l'unico possibile prima dell'entrata in funzione dei metodi di osservazione sismografica moderni (dall'inizio del XX sec.) ed è ancora applicata ai terremoti più antichi o comunque a quelli sui quali non si hanno informazioni strumentali.
Per ipocentro strumentale di un terremoto si intende il punto della faglia in cui la frattura che ha dato origine al terremoto stesso ha avuto inizio, per poi propagarsi a tutta la faglia. Per terremoti di notevole entità, prodotti da faglie di dimensioni rilevanti, l'epicentro strumentale può discostarsi notevolmente da quello macrosismico, che in genere corrisponde alla zona della superficie terrestre più prossima alla parte della faglia che ha subito la maggiore dislocazione o che ha raggiunto la minore profondità. Esistono anche casi nei quali i massimi effetti di un terremoto sono stati riscontrati a notevole distanza dall'epicentro strumentale a causa delle proprietà di risposta dei terreni alle oscillazioni sismiche in particolari siti.
I primi metodi per la determinazione dell'ipocentro e dell'epicentro di un terremoto erano di natura grafica. Il sismologo doveva disporre di almeno tre stazioni sismografiche che avessero registrato l'evento da localizzare. Dai rispettivi sismogrammi si doveva determinare la distanza tra l'ipocentro e la stazione stessa in base alla differenza tra il tempo d'arrivo delle onde P (più veloci) e delle onde S (più lente) moltiplicata per un opportuno coefficiente di proporzionalità (approssimativamente pari a 7 km/s). A questo punto, tracciando su una carta geografica a scala opportuna i cerchi che avevano per centro le stazioni e per raggio le distanze ipocentrali così calcolate, si poteva determinate l'epicentro dall'intersezione delle corde determinate a loro volta dall'intersezione di tali cerchi a due a due. La profondità ipocentrale si calcolava mediante il teorema di Pitagora, conoscendo l'ipotenusa (distanza ipocentrale) e il cateto (distanza epicentrale) del triangolo rettangolo avente per vertici l'ipocentro, l'epicentro e una delle stazioni.
Oltre a quello di non richiedere calcoli complicati, il metodo sopra descritto aveva il vantaggio di non dipendere dalla determinazione del tempo di arrivo assoluto delle onde sismiche alle stazioni, ma solo della differenza di due tipi di onde a ciascuna stazione. Così, esso era utilizzabile anche quando la sincronizzazione degli orologi nelle stazioni sismografiche non era possibile in maniera sufficientemente precisa. Dalla fine degli anni Sessanta del Novecento, con la disponibilità di orologi elettronici sincronizzati mediante ricevitori radio e di mezzi di calcolo elettronico sufficientemente potenti, si è affermato l'uso di metodi di calcolo ipocentrale analitici. Sia pure con numerose possibili varianti, questi metodi, derivati dall'algoritmo originale dovuto a Hans W. Geiger (1912), si basano tutti sulla minimizzazione delle differenze tra tempi di arrivo delle onde P osservati alle stazioni sismografiche e i medesimi tempi calcolati sull'ipotesi di un ipocentro prefissato e di un modello di velocità noto. Mediante approssimazioni successive, l'algoritmo giunge alla localizzazione (comprendente l'istante di partenza delle onde sismiche) che meglio si accorda con l'insieme di tutte le osservazioni.
I moderni elaboratori elettronici, utilizzando i segnali in forma digitale provenienti da una rete sismografica, sono ora in grado di localizzare i terremoti in maniera automatica entro pochi secondi dal loro accadimento. Queste informazioni possono essere molto utili per gli interventi della protezione civile.
Intensità dei terremoti
La 'grandezza' di un terremoto è stata inizialmente quantificata, dalla fine del XIX sec., con le scale d'intensità. Esse erano riferite soltanto agli effetti del sisma ed erano definite mediante gradi interi. Fra le prime scale d'intensità vanno ricordate quelle a 10 gradi dovute a Rossi e Forel (1883) e a Giuseppe Mercalli (1897). Lo stesso Mercalli ha esteso la scala a 12 gradi nel 1904. Successivamente essa è stata integrata con definizioni aggiuntive da Adolfo Cancani e da August Sieberg, fino a essere accettata come standard internazionale con la denominazione di scala MCS (Mercalli-Cancani-Sieberg). È stato rilevato che le scale d'intensità, tra le quali la MCS, rispecchiano, sia pure in maniera involontaria, un andamento logaritmico dei valori dell'accelerazione di picco del suolo prodotti dal terremoto. L'innalzamento di un grado corrisponde, infatti, approssimativamente al raddoppiamento di tale accelerazione. A titolo d'esempio, il VI grado corrisponde a circa 6/100 dell'accelerazione di gravità (60 cm/s2), il VII a 12/100 (120 cm/s2) e l'VIII a 25/100 (250 cm/s2).
L'intensità, riferendosi agli effetti di un terremoto, ha valori che tendono a decrescere allontanandosi dall'epicentro macrosismico; quindi, per uno stesso terremoto, si avranno vari valori di intensità, a partire da quella massima, per arrivare al I grado MCS, dove il terremoto non è avvertito affatto. In sismologia è prassi comune tracciare mappe dove sono riportati i valori dell'intensità di un determinato terremoto rilevati in luoghi e centri abitati diversi. Le linee che si possono tracciare su una mappa di questo tipo per separare i punti caratterizzati da gradi di intensità diversi, che in genere sono linee chiuse che circondano l'epicentro, sono chiamate isosisme (o anche isosiste). Le mappe delle isosisme hanno un grande valore negli studi sugli effetti dei terremoti volti alla mitigazione del rischio sismico.
Una formula semplificata che descrive l'attenuazione dell'intensità I (MCS) con la distanza epicentrale Δ è quella dovuta a Archie Blake:
[1] formula
dove I0 è l'intensità all'epicentro, h è la profondità dell'ipocentro, e s è un parametro dipendente dalle condizioni geologiche il cui valore è compreso tra 3 e 6. Questa formula è usata anche per determinare la profondità ipocentrale, una volta note le altre grandezze.
Magnitudo
Dal 1935, in sismologia è stata introdotta da Charles F. Richter la nozione di magnitudo, una grandezza a valori continui basata sull'ampiezza delle registrazioni sismografiche e ragguagliata con la distanza dall'epicentro, in maniera da fornire una valutazione legata univocamente all'energia rilasciata dalla sorgente del terremoto. La prima definizione di magnitudo, detta magnitudo locale, è stata data tramite la formula
[2] M = log(A) − log[A0(Δ)]
dove A è l'ampiezza di picco del sismogramma registrato da un sismografo campione, detto Wood-Anderson, a una distanza epicentrale Δ dall'epicentro, e A0(Δ) è l'ampiezza del sismogramma di un terremoto di magnitudo M=0 registrato alla stessa distanza epicentrale. La funzione A0(Δ) fu ricavata empiricamente da Richter, e pubblicata in forma di tabella, dall'osservazione dell'ampiezza dei sismogrammi registrati a varie distanze epicentrali (comprese fra 0 e 600 km) per alcuni terremoti avvenuti in California. Il terremoto di magnitudo M=0 è definito a sua volta in maniera assoluta come quel terremoto che produce sul sismografo campione Wood-Anderson una registrazione di ampiezza pari a 0,001 mm alla distanza epicentrale di 100 km. A un terremoto che viene registrato con ampiezza minore di quello di magnitudo M=0 viene assegnata una magnitudo negativa. Si noti che anche la magnitudo, come l'intensità, è una grandezza logaritmica.
Nuove definizioni di magnitudo si sono successivamente aggiunte all'originale, per adattarsi all'osservazione di diversi tipi di onde, a diversi intervalli di distanze epicentrali (in particolare per le distanze telesismiche, ovvero quelle maggiori di 2000 km), e all'uso di strumentazione sismografica diversa. Tra le magnitudo stimate a distanze telesismiche, vanno ricordate la magnitudo misurata dalle onde di volume (più comunemente le onde P osservate tra 2000 e 11.000 km di distanza) aventi circa un secondo di periodo (mb) e quella misurata dalle onde superficiali (da 2000 a 20.000 km di distanza) aventi circa 20 s di periodo (Ms).
Per l'osservazione di terremoti in ambito strettamente locale (distanza epicentrale entro circa 200 km) è diventato popolare anche l'uso della magnitudo durata (Md), il cui concetto è originato dall'osservazione che i sismogrammi dei vari terremoti hanno una coda tanto più lunga quanto più grande è l'energia (e la magnitudo) del terremoto. Nel 1971 William H.K. Lee e alcuni suoi collaboratori hanno ricavato sperimentalmente per la California la seguente relazione, che è diventata la definizione di magnitudo durata:
[3] Md = − 0,87 + 2logτ + 0,0035Δ
dove τ è la durata del sismogramma in secondi e Δ è la distanza epicentrale in chilometri.
Non deve stupire che con l'applicazione di definizioni di magnitudo tra loro diverse si giunga spesso, per uno stesso evento sismico, a stime di valori anche molto discordanti fra loro. Negli anni Settanta, con la comparsa dei sismografi a banda larga, è stato possibile orientarsi verso una nuova definizione di magnitudo, il cui valore prende origine da una grandezza fisica quantificabile oggettivamente come il momento sismico e che per questo viene chiamata magnitudo momento. La magnitudo momento offre, fra l'altro, il vantaggio di non saturarsi per valori alti della scala, mentre ciò limita, per esempio, a valori di 6,5÷7 la magnitudo mb e a valori di 8,0÷8,5 la magnitudo Ms. Per alcuni terremoti del XIX e XX sec., e per il terremoto di Sumatra del dicembre 2004, la stima della magnitudo momento ha fornito, discostandosi in questo dalle stime tradizionali, valori superiori a 9,0.
La magnitudo è stata messa in relazione, dallo stesso Richter in collaborazione con Beno Gutenberg, con l'energia rilasciata dalla sorgente del terremoto al suo ipocentro. Per mezzo di considerazioni fisiche abbastanza semplici, i due sismologi americani hanno calcolato che tra l'energia Es in joule emessa dal terremoto e la magnitudo Ms esiste la relazione:
[4] log(Es) = 4,8 + 1,5Ms.
In base a questa relazione, è possibile redigere una tabella che illustri la corrispondenza tra magnitudo di un terremoto, energia elastica rilasciata e quantità di tritolo che si dovrebbe far esplodere per liberare la stessa energia sotto forma di onde elastiche (tab. 1).
Sebbene la magnitudo debba essere intesa come una grandezza che quantifica un terremoto alla sua origine, mentre l'intensità è una stima degli effetti da esso prodotti in un particolare sito, è diventata consuetudine ipotizzare una relazione tra queste due grandezze, limitando il concetto di intensità semplicemente a quella rilevata all'epicentro. L'intensità di un terremoto di data magnitudo al suo epicentro dipende fortemente dalla profondità dell'ipocentro e dalle caratteristiche geologiche del sito. Per una profondità ipocentrale tipica dell'Appennino (circa 10 km) tale relazione può essere espressa come:
[5] I = 2,5M − 4,0.
La relazione ora vista può essere invertita per ricavare la magnitudo di terremoti avvenuti nel passato, per i quali non esistono registrazioni sismografiche. Tale magnitudo è detta magnitudo macrosismica.
Modelli meccanici dei terremoti
Un modello di terremoto semplice, ma più realistico di quello puntiforme, è quello a dislocazione piana. In questo modello il terremoto avviene quando si verifica una rottura, lungo una superficie piana di faglia, al raggiungimento del limite di resistenza meccanica. Il fenomeno è descritto quantitativamente da un certo numero di parametri, alcuni dei quali legati tra loro in base ad assunzioni semplificative. Tra questi parametri vanno segnalati: (a) le dimensioni della sorgente, ovvero il suo raggio r, se si immagina una frattura circolare; la sua lunghezza L e la sua larghezza W, se si immagina una frattura di forma rettangolare; (b) la superficie S, pari a 4πr2, per una sorgente circolare, e LW per una sorgente rettangolare; (c) l'entità della dislocazione Δu, o meglio il suo valore medio (la dislocazione deve essere nulla sul perimetro della frattura); (d) il rilascio di sforzo sulla faglia Δσ al raggiungimento di una nuova situazione di equilibrio al termine della frattura; (e) l'energia elastica Es, energia emessa sotto forma di onde sismiche (inferiore all'energia potenziale complessivamente rilasciata dalla dislocazione, in quanto una parte considerevole di essa viene dissipata per attrito sotto forma di calore); (f) il momento sismico M0 del terremoto definito come M0=μΔuS, dove μ è il modulo elastico di taglio delle rocce interessate dalla frattura (per la crosta terrestre il modulo elastico di taglio è circa pari a 3∙104 MPa).
La teoria dell'elasticità consente di dimostrare che nel caso di una sorgente circolare fra le grandezze sopra citate esistono le seguenti relazioni:
[6] formula
[7] formula.
[8] formula.
Per sorgenti rettangolari nelle quali la dimensione più corta W sia molto minore di L, valgono invece le relazioni:
[9] formula.
[10] formula.
Fra i vari parametri che caratterizzano la sorgente di un terremoto quelli misurabili più o meno direttamente dalle osservazioni sismografiche sono il momento sismico M0 e le dimensioni lineari r. Per terremoti di magnitudo compresa fra 3 e 8 è stato rilevato che il momento sismico varia approssimativamente tra 5∙1013 e 1021 N∙m, mentre le dimensioni della faglia variano da 100 m a 300 km. Le formule sopra elencate consentono di determinare gli altri parametri.
Si è notato, pertanto, che il rilascio di sforzo varia entro limiti molto più ristretti rispetto a quelli del momento sismico e delle dimensioni lineari, risultando tipicamente compreso tra 1 MPa e 10 MPa. La spiegazione di questa circostanza risiede nel fatto che la grandezza di un terremoto è direttamente legata all'estensione della superficie di faglia fratturata (variabile su una scala di molti ordini di grandezza), mentre il rilascio di sforzo è una quantità più strettamente collegata alle proprietà fisiche dei materiali, che non variano eccessivamente da un punto all'altro della crosta terrestre.
Assumendo per il rilascio di sforzo un valore ipotetico pari a Δσ=3 MPa, le relazioni già viste portano alla determinazione della dislocazione media per un terremoto di cui si conoscano le dimensioni lineari. Si ottiene che questa dislocazione è proporzionale alla dimensione più corta della sorgente, con un coefficiente di proporzionalità dell'ordine di 5/100.000. Così, per esempio, si ritiene che un terremoto che avvenga per frattura di una faglia larga 10 km formi sulla faglia stessa una dislocazione di circa 50 cm.
Per quanto riguarda l'energia liberata dal terremoto sotto forma di onde elastiche, sotto la stessa ipotesi di un rilascio di sforzo pari a Δσ=3 MPa, si ottiene
[11] Es = 0,5∙10−4 M0.
Si noti che sia l'energia Es sia il momento sismico M0 hanno le stesse unità di misura, ma con significato fisico diverso.
Ricordando che l'energia Es è legata alla magnitudo tramite l'equazione [4], otteniamo la formula per il calcolo approssimato del momento sismico di un terremoto di data magnitudo:
[12] log(M0) = 9,1 + 1,5 M.
Questa breve rassegna ha permesso di mettere in relazione una serie di parametri caratterizzanti un modello fisico di sorgente sismica, concludendo che: (a) si può ritenere che l'abbassamento di sforzo causato da un terremoto su una faglia non presenti ampie variazioni, mantenendosi in un intervallo dell'ordine di 1÷10 MPa; (b) il momento sismico e l'energia sono le quantità che variano maggiormente nella quantificazione delle sorgenti sismiche: queste due grandezze sono proporzionali al volume di roccia occupato dalla sorgente sismica e aumentano con proporzione geometrica di circa trenta volte per ogni unità di magnitudo; (c) l'area di una faglia messa in movimento da un terremoto aumenta anch'essa con proporzione geometrica di circa un fattore dieci per ogni unità di magnitudo; (d) la dislocazione sulla faglia dislocata dal terremoto è essenzialmente condizionata dalla dimensione minore della frattura sulla faglia con un fattore di scala piuttosto costante.
Statistica dei terremoti
Fin dai primi anni dalla definizione di magnitudo ci si accorse che il numero di terremoti di piccola entità era molto maggiore di quello dei grandi terremoti. Come si può vedere dalla tab. 2, valida per i terremoti di tutto il mondo, questo numero aumentava di circa un fattore dieci per ogni unità di magnitudo più bassa.
I già citati sismologi americani Gutenberg e Richter, riprendendo studi già condotti negli anni precedenti, introdussero una relazione tra magnitudo e numero di terremoti con magnitudo uguale o superiore a quel dato valore di soglia:
[13] N = 10a − bM
dove a è il logaritmo del numero totale di terremoti di magnitudo uguale o superiore a 0 per l'area e il periodo di tempo considerati, e b è un coefficiente valido per la zona considerata, solitamente prossimo a 1. Questa formula, che è nota col nome di legge di Gutenberg e Richter, nonostante la sua natura totalmente empirica e la mancanza di legami con leggi fisiche preesistenti, si è mostrata nel tempo come legge di straordinaria validità, applicabile in generale alla sismicità di regioni diverse in una vasta gamma di situazioni (tranne che in qualche specifico caso di sismicità vulcanica). Studi moderni hanno messo in risalto come tale legge possa provenire dalle proprietà frattali del fenomeno di autoorganizzazione dell'attività sismica, definito come processo a criticalità organizzata, un tipo di processo riscontrabile anche in altri settori delle scienze naturali. La fig. 5 riporta, come esempio, la distribuzione del numero di terremoti rispetto alla magnitudo lungo un periodo di vent'anni in Italia; l'andamento osservato è prossimo a quello teorico mostrato con una linea retta. Tuttavia, la flessione della curva verso il basso, osservabile alle magnitudo prossime a 6, evidenzia uno scostamento rispetto alla pura teoria. Tale scostamento può indicare una reale limitazione della magnitudo massima dei terremoti nella regione considerata, con conseguenze positive nei riguardi della pericolosità sismica.
Come si può osservare dalla tab. 2, mentre il numero di terremoti cresce esponenzialmente con l'abbassarsi della magnitudo, questo non avviene per l'energia, o anche per il momento sismico, complessivamente rilasciati dagli stessi terremoti. Infatti, integrando la relazione magnitudo-frequenza di Gutenberg e Richter con la formula che fornisce l'energia sismica liberata dal singolo terremoto, si ottengono valori che scendono con la magnitudo. Sono quindi pochi i terremoti di maggiore violenza che da soli forniscono il maggior contributo in termini di rilascio di energia sismica. La quantità totale di energia sismica liberata nel mondo è limitata dalla magnitudo massima dei terremoti (di poco superiore a 9,0), legata alle dimensioni finite delle grandi strutture attive del globo.
Dalla legge di Gutenberg e Richter si può facilmente ricavare che la magnitudo media di un campione completo di N terremoti con magnitudo minima M0 non dipende dal loro numero ed è data da:
[14] formula.
Questa formula fornisce anche un modo conveniente per determinare il valore del parametro b in una data regione sismica a partire da un campione sufficientemente numeroso di terremoti osservati.
L'espressione periodo di ritorno di un terremoto indica il valore medio del tempo intercorrente fra un evento e il successivo. Il periodo di ritorno Tr(M) è ovviamente funzione della magnitudo M scelta per l'analisi. Una stima del periodo di ritorno è data dal rapporto fra il tempo di osservazione T0 e il numero di eventi osservati N(M):
[15] formula.
Tale stima è abbastanza accurata se il numero di terremoti osservati è sufficientemente elevato. Come si può facilmente notare, il periodo di ritorno cresce esponenzialmente al crescere della magnitudo considerata.
Noto il periodo di ritorno per i terremoti di magnitudo pari o superiore a M, la statistica permette di calcolare la probabilità che tale magnitudo venga superata almeno una volta in un tempo T.
[16] formula.
Pericolosità sismica e prevedibilità a lungo termine dei grandi terremoti
Avendo come fine ultimo quello di mitigare i gravi danni che esso talvolta produce sia sulle persone sia sulle cose, il terremoto è studiato per conoscere la pericolosità sismica di una data zona, concetto legato sia alla probabilità di accadimento sia agli effetti del terremoto.
Mentre la pericolosità sismica dipende totalmente dalla natura fisica dei fenomeni legati al terremoto, il rischio sismico (definito come costo totale da pagare per reintegrare il valore dei beni ridotto a causa dei terremoti) è un concetto legato anche al valore e alla vulnerabilità dei beni esposti all'evento, nonché al costo delle eventuali misure di prevenzione adottate. Sembra ovvio ricordare che lo studio del rischio sismico presuppone quello della pericolosità sismica.
La pericolosità sismica di un sito rappresenta la probabilità che un dato evento si verifichi in un intervallo di tempo prestabilito (Probabilistic seismic hazard assessment, PSHA). Essa esprime la probabilità che un valore di pericolosità, espresso da un parametro di moto del suolo, come l'accelerazione massima (Peak ground acceleration, PGA) venga superato in un dato sito entro un periodo di tempo fissato. La valutazione della pericolosità sismica in termini probabilistici comporta, secondo il metodo introdotto da Allin C. Cornell nel 1968 e largamente seguito fino ai nostri giorni, la conoscenza di tutte le caratteristiche principali delle sorgenti sismogenetiche potenzialmente pericolose per l'area di interesse, e di un appropriato modello di attenuazione dell'intensità del terremoto in funzione della distanza epicentrale.
Il metodo di Cornell e le sue varianti presuppongono che si conosca il periodo di ritorno, riferito a ciascuna sorgente sismica potenzialmente pericolosa. Questo tipo di informazione si può ottenere seguendo due approcci distinti: (a) quello storico-statistico, che consiste nell'analisi del catalogo sismico della regione considerata, assumendolo come completo per il periodo di tempo più lungo possibile; (b) quello fisico-geologico, che si basa sulla determinazione del rateo di deformazione su ciascuna faglia sismogenetica e sulla dislocazione media del terremoto caratteristico su tali faglie.
Nell'approccio storico-statistico si prendono in esame i periodi di ricorrenza con cui i terremoti di data magnitudo accadono in determinate aree. A questo fine, un settore della sismologia, denominato sismologia storica, si dedica al ritrovamento, all'analisi e all'archiviazione delle notizie storiche che si possono reperire riguardo ai terremoti dell'antichità. Purtroppo, anche in Paesi di antiche tradizioni storiche come l'Italia, la Grecia o la Cina, i periodi di tempo a partire dai quali ci provengono notizie sui terremoti (dell'ordine di duemila anni al massimo) sono relativamente brevi per poterne trarre valutazioni statistiche quantitative. Inoltre, si deve considerare che le notizie sui terremoti, anche se reperibili, sono, specialmente per quelli dell'epoca medioevale o precedenti, piuttosto vaghe o addirittura distorte, a causa dell'ambito soprannaturale in cui venivano inquadrati tali fenomeni.
L'approccio fisico-geologico presenta anch'esso difficoltà che conducono a risultati caratterizzati da grande incertezza. I ratei di deformazione in atto nelle aree sismiche attive in Italia sono così modesti (dell'ordine di 0,1÷1 mm/anno) che occorrono decine di anni per averne una stima anche approssimativa con le tecniche di misurazioni geodetiche più efficienti (basate sul sistema satellitare GPS, Global positioning system). Inoltre non esiste la certezza che la deformazione misurata geodeticamente si liberi tutta in forma di energia sismica, attraverso i soli terremoti caratteristici. Parte della deformazione, in proporzione sconosciuta, potrebbe essere liberata da scorrimento asismico (creep) o dall'effetto congiunto di terremoti di magnitudo inferiore.
Con l'obiettivo di coprire tali lacune si è sviluppato, da pochi decenni, un nuovo settore della sismologia, chiamato paleosismologia, che sta apportando informazioni preziose sui terremoti avvenuti in epoche preistoriche, risalendo fino ad alcune decine di migliaia di anni fa. La paleosismologia si basa sull'osservazione di tracce geologiche che i forti terremoti del passato hanno lasciato sull'ambiente e che si riscontrano ancora oggi, in superficie, o a pochi metri di profondità. Uno dei metodi di datazione di tali reperti è quello del 14C.
In Italia la paleosimologia ha consentito di affermare che alcuni importanti terremoti (come per es., quello avvenuto nel 1915 ad Avezzano e quello del 1980 in Irpinia) sono stati preceduti, con intervalli variabili tra i 1500 e i 3000 anni, da altri terremoti che si sono manifestati negli stessi luoghi e con caratteristiche molto simili fra loro. Queste osservazioni conducono a pensare che tali terremoti si possano considerare come caratteristici delle strutture studiate.
Molti sismologi ritengono che il terremoto caratteristico ricorra sulla stessa struttura sismogenetica a intervalli di tempo pseudo-periodici, caratteristici della struttura stessa, anziché distribuirsi nel tempo in maniera casuale. Se così fosse, le conseguenze nella valutazione della pericolosità sismica sarebbero importantissime, perché una zona potrebbe ritenersi sicura nei tempi immediatamente successivi al suo terremoto caratteristico, mentre in seguito la pericolosità andrebbe crescendo con l'approssimarsi al tempo di ricorrenza tipico del terremoto.
In base a un modello piuttosto semplice, quello dell'elastic rebound introdotto da Harry F. Reid nel 1910, la semi-periodicità del terremoto caratteristico potrebbe essere spiegata mediante un meccanismo di accumulo lento e di liberazione improvvisa dell'energia elastica connessa agli sforzi di origine tettonica che operano ai margini delle zolle litosferiche. Negli ultimi decenni si è iniziato a comprendere che le cose in realtà non sono così semplici. Mentre l'ipotesi del terremoto caratteristico sembra essere confermata piuttosto bene in senso retrospettivo dalla cronologia dei terremoti avvenuti nel passato in alcune zone del mondo, la stessa ipotesi, applicata sistematicamente in senso predittivo alla sismicità globale degli ultimi due decenni, ha finora dato risultati di scarso significato statistico.
Precursori e prevedibilità a breve termine dei terremoti
Anche se la previsione deterministica di un terremoto è stata considerata sempre un obiettivo praticamente irraggiungibile, una cospicua serie di osservazioni e di studi è stata rivolta all'individuazione di fenomeni, detti precursori, che, osservati prima dei terremoti, ne possano far presagire l'imminente accadimento. Questi fenomeni sono stati cercati in campo geofisico, geochimico e anche biologico. All'inizio degli anni Ottanta la letteratura riportava già decine e decine di osservazioni classificate come precursori, così che si era diffusa l'opinione che la previsione dei terremoti sarebbe stata utilizzabile ai fini pratici entro pochi decenni. Tuttavia la mancanza di risultati concreti ha condotto alla perdita dell'ottimismo iniziale e alla diminuzione di interesse per l'indagine retrospettiva sui precursori.
Pur rimanendo la previsione dei terremoti un tema di ricerca estremamente importante, l'atteggiamento dei sismologi nell'ultimo decennio è diventato molto più cauto e le ricerche sono orientate soprattutto alla descrizione quantitativa dei complicati processi dai quali i terremoti vengono enucleati. Secondo una corrente di pensiero relativamente recente, la litosfera sarebbe ovunque e in qualunque istante autoorganizzata in uno stato di equilibrio critico prossimo al punto di fratturazione. Solo raramente, e in alcuni punti particolari, lo stato di equilibrio viene perturbato da cause diverse e più rapide del lento accumulo di sforzo tettonico, e in quei punti prende avvio la dislocazione che si propaga sulla faglia e dà origine al terremoto. A causa del comportamento caotico del sistema, in questo modello, né l'istante di inizio di un terremoto, né la sua magnitudo sono deterministicamente prevedibili.
Tra le cause di perturbazione dello stato di sforzo della litosfera, riconosciute come possibili stimolatori dell'attività sismica, ci sono le maree terrestri, la migrazione di fluidi, le attività antropiche (come le esplosioni nucleari o la coltivazione di giacimenti petroliferi), ma soprattutto ci sono i terremoti stessi. Applicando la teoria dell'elasticità è possibile calcolare che al verificarsi di ogni terremoto, lo stato di tensione sulle faglie in una vasta zona circostante subisce una variazione che può sia favorire sia inibire la loro successiva frattura. Lo stato delle conoscenze sull'argomento ha subito notevoli sviluppi nell'ultimo decennio. La legge costitutiva (rate and state), introdotta da James H. Dieterich nel 1994 e basata su esperienze di laboratorio condotte sull'attrito tra superfici di campioni di rocce, consente di spiegare fisicamente il fenomeno delle sequenze di repliche che seguono solitamente i terremoti come fenomenologia dovuta al comportamento statistico di un insieme di innumerevoli faglie.
Per quanto riguarda le metodologie statistiche adottate per la verifica di ipotesi di previsione, l'indirizzo più moderno si rivolge alla stima, sotto determinate ipotesi e condizioni, della probabilità di occorrenza di un evento di una certa magnitudo in funzione del luogo e del tempo considerati. Questa formulazione viene detta previsione sinottica, in analogia a quanto avviene per le previsioni meteorologiche. In questo modo, la validità di un metodo di previsione può essere confermata non solo dall'aumento di probabilità in una zona dove il terremoto realmente si verifica, ma anche dalla sua diminuzione nelle zone dove invece esso non compare. Un parametro statistico mediante il quale è possibile dare un'indicazione della qualità di un metodo di previsione è il guadagno di probabilità. Tale parametro viene definito come il rapporto fra il rateo di eventi che avvengono negli intervalli spazio-temporali che tale metodo individua come volume di allarme e il corrispondente rateo medio osservato nell'intera estensione spazio-temporale della regione in esame.
Ovviamente l'applicazione del concetto di guadagno di probabilità alla valutazione di un metodo di previsione presuppone che il metodo di previsione sia formulato in maniera da definire chiaramente e oggettivamente tutti i parametri degli eventuali allarmi, includendo, oltre all'estensione dell'area di allarme e alla sua durata, anche la magnitudo minima cui l'allarme si riferisce.
Mitigazione del rischio sismico
Nell'attesa dell'ipotetica possibilità di prevedere i terremoti, il modo più concreto che si ha oggi a disposizione per mitigare il rischio sismico è quello di abbassare la vulnerabilità dei manufatti esposti al terremoto. Questo si può realizzare, per esempio, scegliendo opportunamente i siti ove costruire tali manufatti o progettando strutture più robuste a parità di costi, o con un costo aggiuntivo ragionevole. A tal fine occorre conoscere con esattezza le caratteristiche delle sollecitazioni che i terremoti impartiranno alle strutture da progettare o da rinforzare. I danni che una struttura può subire da parte del terremoto non dipendono soltanto dalla PGA, ma anche dalle frequenze che compongono la sollecitazione nel suo insieme e dalla durata della sollecitazione stessa. È universalmente riconosciuto che, in occasione di un terremoto, a parità di distanza dalla sorgente sismica, siti con differenti caratteristiche geotecniche rispondono in modo molto diverso alle vibrazioni del substrato roccioso. In genere i terreni poco consolidati, come le alluvioni recenti o le sabbie, tendono a entrare in risonanza e ad amplificare le oscillazioni provenienti dagli strati inferiori più rigidi. In alcuni casi, il fenomeno della liquefazione mette addirittura in pericolo la stabilità statica dei manufatti. Le tecniche di calcolo moderne, confermate da una grande serie di osservazioni sperimentali, consentono ora di prevedere con esattezza il comportamento degli edifici da parte di ipotetici terremoti in zone con caratteristiche geotecniche note. Ciò consente di scegliere tra due siti vicini quello più sicuro, oppure, in ogni caso, di adottare le norme di progettazione antisimica più idonee a resistere alla frequenza dominante del terremoto ipotizzabile. In ingegneria sismica si fa uso del cosiddetto spettro di risposta per ottenere una stima dell'input sismico da utilizzare nella fase di progetto di una struttura. Edifici più bassi tendono a risentire maggiormente delle frequenze più alte (2÷5 Hz) e quelli più alti delle frequenze più basse (0,5÷1 Hz). La risonanza alle oscillazioni deve essere evitata con l'introduzione di elementi dissipatori dell'energia (per es., le tamponature) che fanno da smorzatori. Per gli edifici già esistenti i progressi in ingegneria sismica consentono oggi, di mettere in atto accorgimenti a basso costo che ne riducono sostanzialmente la vulnerabilità.
Nei Paesi economicamente più sviluppati la mitigazione del rischio sismico è oggetto di normativa specifica, in continua evoluzione, che prescrive le misure da seguire a questo fine, soprattutto per quanto riguarda la costruzione di nuovi edifici in zone riconosciute come sismiche.
Bibliografia
Blake 1941: Blake, Archie, On the estimation of focal depth from macroseismic data, "Bulletin of the Seismological Society of America", 34, 1941, pp. 225-231.
Cornell 1968: Cornell, C. Allin, Engineering seismic risk analysis, "Bulletin of the Seismological Society of America", 58, 1968, pp. 1583-1606.
Dieterich 1994: Dieterich, James H., A constitutive law for rate of earthquake production and its application to earthquake clustering, "Journal of geophysical research", 99, 1994, pp. 2601-2618.
Geiger 1912: Geiger, Ludwig, Probability method for the determination of earthquake epicenters from the arrival time only, "Bulletin of the Saint Louis University", 8, 1912, pp. 56-71.
Gutenberg, Richter 1942: Gutenberg, Beno - Richter, Charles F., Earthquake magnitude, intensity, energy, and acceleration, "Bulletin of the Seismological Society of America", 32, 1942, pp. 163-191.
Hanks, Kanamori 1979: Hanks, Thomas C. - Kanamori, Hiroo, A moment magnitude scale, "Journal of geophysical research", 84, 1979, pp. 2348-2350.
Lee 1972: Lee, William H.K. - Bennett, R.E. - Meagher, Karen L., A method of estimating magnitude of local earthquakes from signal duration, U.S. Geological Survey, Open filereport, 79-1621, 1972, pp. 1-43.
Reid 1910: Reid, Harry F., The mechanics of the earthquake, The California earthquake of april 18, 1906: Report of the State Investigation Commission, Washington D.C., Carnegie Institution of Washington, 1910.
Richter 1935: Richter, Charles F., An instrumental earthquake magnitude scale, "Bulletin of the Seismological Society of America", 25, 1935, pp. 1-32.
Sieberg 1930: Sieberg, August, Geologie der Erdbeben, Berlin, Borntraeger, 1930.