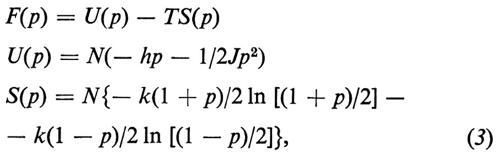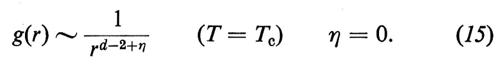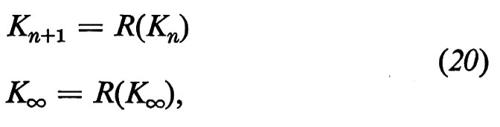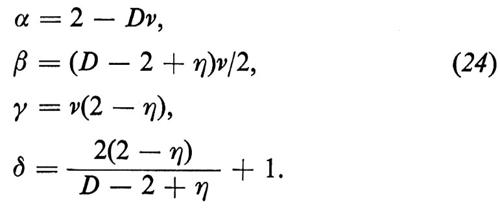Transizioni di fase
Transizioni di fase
SOMMARIO: 1. Definizione di fase e di transizione di fase. 2. Classificazione delle transizioni di fase. 3. Diagramma delle fasi. 4. Transizioni di fase del prim'ordine e stati metastabili. 5. Ordine e disordine. 6. Teoria microscopica e termodinamica delle transizioni di fase. 7. Transizioni di fase del second'ordine: a) esponenti critici; b) il gruppo di rinormalizzazione. □ Bibliografia.
1. Definizione di fase e di transizione di fase
Un sistema fisico subisce una transizione di fase se, al variare di alcuni parametri di controllo (per esempio la pressione, la temperatura, il campo magnetico, ecc.), passa da una fase a un'altra fase (v. Landau e Lifschitz, 1971).
Fin dalle scuole elementari ci è noto che quasi tutte le sostanze possono esistere nelle tre fasi: gassosa, liquida e solida; l'acqua, per esempio, mentre a temperatura ambiente è liquida, a bassa temperatura è solida (ghiaccio) e ad alta temperatura è gassosa (vapor acqueo).
Tuttavia i concetti di fase e di transizione di fase sono più ricchi di quanto questo semplice esempio possa far pensare. In prima approssimazione possiamo caratterizzare una fase di un sistema fisico in base alla presenza o all'assenza di alcuni fenomeni.
1. Un corpo è solido se resiste alle deformazioni e mantiene naturalmente la sua forma in assenza di forze esterne; quando viene leggermente deformato si genera una forza elastica che tende a ripristinare la situazione precedente. Al contrario un corpo è fluido (gas o liquido) se non ha nessuna forma naturale e basta una forza esterna estremamente piccola per deformarlo. La transizione di fase dalla fase solida alla fase fluida avviene al punto di fusione o di sublimazione: il solido, riscaldato, diventa fluido.
2. Il ferro (come tutte le cosiddette sostanze ferromagnetiche) gode delle ben note proprietà magnetiche al di sotto della temperatura di Curie (circa 700 °C), mentre ne è assolutamente privo a temperature superiori (v. Kittel, 1966). A seconda della temperatura il ferro può stare in due fasi: in una fase magnetica (più propriamente ferromagnetica) o in una fase non magnetica (più propriamente paramagnetica). Se viene scaldato partendo dalla temperatura ambiente, passa dalla fase magnetica alla fase non magnetica quando raggiunge la temperatura di Curie.
3. Alcuni materiali (per esempio l'alluminio, il niobio, il piombo, ecc.) a temperature di qualche grado sopra lo zero assoluto diventano superconduttori: la loro resistenza elettrica si annulla e una corrente elettrica può circolarvi anche in assenza di un campo elettrico esterno (v. Lynton, 1962); a temperatura ambiente, invece, sono conduttori normali con resistenza non nulla e seguono l'usuale legge di Ohm. Questi materiali possono trovarsi o nella fase superconduttrice o nella fase normale.
4. Se si immerge un materiale superconduttore in un campo magnetico non eccessivamente forte, il superconduttore reagisce creando sulla propria superficie correnti che generano un secondo campo magnetico, in modo che il campo magnetico totale all'interno del superconduttore sia nullo. In altre parole il superconduttore espelle il campo magnetico. Uno studio più dettagliato di questo fenomeno ha messo in evidenza l'esistenza di due tipi di superconduttori. Nei superconduttori del primo tipo il campo magnetico esterno, quando supera un valore critico, riesce a penetrare all'interno del materiale distruggendone la superconduttività: in questo caso la transizione da superconduttore a conduttore è causata dalla variazione del campo magnetico.
Nei superconduttori del secondo tipo la situazione è più complicata (v. de Gennes, 1966). Quando il campo magnetico supera un primo valore critico, penetra dentro il superconduttore, ma viene canalizzato in linee di flusso; le regioni dove il campo magnetico è presente non sono più superconduttrici, ma il resto del materiale rimane superconduttore. In questa situazione di compromesso (fase mista) il campo magnetico penetra (almeno parzialmente) nel materiale, ma la superconduttività non scompare. Via via che il campo magnetico aumenta, le linee di flusso diventano più numerose e la regione superconduttrice diventa più piccola; quando il campo magnetico supera un secondo valore critico, il sistema diventa semplicemente conduttore. Al variare del campo magnetico si verificano due transizioni di fase.
I superconduttori del secondo tipo sono molto importanti tecnologicamente, in quanto la superconduttività viene distrutta solo da campi magnetici molto forti.
5. Altri materiali sono conduttori normali in un certo intervallo di temperature mentre diventano isolanti (a resistenza infinita) in un altro intervallo di temperature (transizione da conduttore a isolante). In altri casi (per esempio silicio con aggiunta una percentuale x di arsenico) il materiale passa da conduttore a isolante al variare della sua composizione stechiometrica (per il silicio il parametro critico è la percentuale x di impurezze di arsenico).
Gli esempi si potrebbero moltiplicare all'infinito: ogni volta che il comportamento qualitativo di un sistema fisico (in uno dei suoi molteplici aspetti) cambia al variare di parametri di controllo (che possono essere la pressione, la temperatura, il campo magnetico, la composizione chimica, ecc.) siamo in presenza di una transizione di fase.
Questa definizione di transizione di fase non è tuttavia completamente soddisfacente. Talvolta le due fasi non sono qualitativamente differenti (in una fase non è presente nessun fenomeno che non sia presente nell'altra fase) ma sono differenti solamente dal punto di vista quantitativo. Per esempio, sia i gas che i liquidi sono fluidi e non ci sono proprietà intrinseche che caratterizzano i liquidi in opposizione ai gas. L'unica differenza fra un gas e un liquido è che a bassa pressione (per esempio alla pressione di 1 atmosfera) i gas sono normalmente estremamente meno densi dei liquidi. Vedremo nel cap. 3 che variando contemporaneamente la pressione e la temperatura è possibile trasformare un liquido in un gas senza soluzione di continuità. Quando, all'aumentare della pressione o al diminuire della temperatura, la densità di un fluido aumenta in maniera discontinua si usa dire che il fluido è passato dalla fase gassosa alla fase liquida, anche se non esiste una definizione intrinseca di gas o di liquido.
Allo scopo di non perdere di generalità, conviene modificare la definizione precedente asserendo che tutte le volte che al variare dei parametri di controllo alcune proprietà del sistema cambiano in maniera brusca si è in presenza di una transizione di fase. Vedremo nel prossimo capitolo che le transizioni di fase si possono classificare secondo il grado di discontinuità con cui le proprietà del sistema cambiano.
Si noti che in questo articolo ci limiteremo a considerare essenzialmente transizioni di fase in sistemi fisici all'equilibrio termico. Fenomeni omologabili alle transizioni di fase sono presenti in sistemi che sono mantenuti distanti dall'equilibrio termico da un flusso costante di energia. Sfortunatamente la comprensione di tali fenomeni non è avanzata come per i sistemi all'equilibrio termico (v. termodinamica irreversibile e sinergetica, dove sono descritti alcuni tentativi di studiare sistemi non all'equilibrio termico).
2. Classificazione delle transizioni di fase
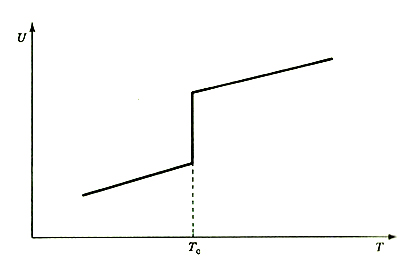
Consideriamo un sistema che subisce una transizione di fase al variare della temperatura: per T <TC il sistema si trova nella fase A, per T > TC nella fase B. Possiamo distinguere due casi principali: a) per passare dalla fase A alla fase B è necessario fornire al sistema una certa quantità di energia, detta ‛calore latente di transizione'. L'esempio tipico è dato dalla transizione solido-liquido: per fondere un grammo di ghiaccio sono necessarie circa 80 calorie; l'energia interna U del sistema è una funzione discontinua della temperatura (v. fig. 1) e la transizione di fase è detta del prim'ordine; b) se invece l'energia interna è una funzione continua della temperatura e quindi il calore latente è nullo, la transizione è di ordine superiore al primo.
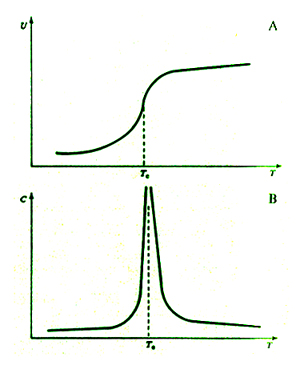
Secondo la classificazione originale si possono distinguere vari sottocasi. Se il calore specifico (la derivata dell'energia interna rispetto alla temperatura) diverge o è discontinuo alla temperatura critica TC (v. fig. 2), la transizione è del second'ordine, altrimenti è di ordine superiore al secondo. In generale, se la derivata di ordine n dell'energia interna rispetto alla temperatura è continua, ma la derivata di ordine n + 1 diverge o è discontinua, la transizione è detta di ordine n + 2. Nel caso in cui l'energia interna sia una funzione della temperatura infinitamente derivabile, ma non analitica nel punto T = TC, la transizione è di ordine infinito.
Molto spesso nella prassi corrente questa classificazione viene semplificata: tutte quelle transizioni che non siano né del prim'ordine né di ordine infinito, sono chiamate transizioni del second' ordine, dato che le transizioni di fase del second'ordine e quelle degli ordini successivi vengono studiate usando tecniche simili.
Esempi classici di transizioni di fase del second'ordine sono le transizioni ferromagnete-paramagnete e superconduttore-conduttore.
Dal punto di vista sperimentale è difficile rilevare l'esistenza di transizioni di fase di ordine infinito, in quanto una funzione infinitamente derivabile si confonde facilmente con una funzione analitica. Le uniche informazioni su queste transizioni (spesso presenti in materiali disordinati) vengono dalla teoria: il loro studio è molto complicato e i risultati ottenuti sono scarsi (v. Griffith, 1969).
Se il parametro che controlla la transizione non è la temperatura, la trattazione è molto simile: basta considerare l'energia libera F (F = U – TS, dove U è l'energia interna ed S l'entropia). In questo caso la derivata di F rispetto al parametro che controlla la transizione gioca un ruolo analogo all'energia interna nel caso precedente (v. Huang, 1967).
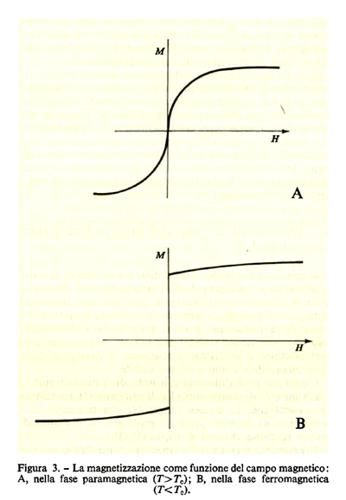
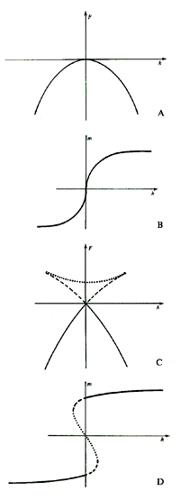
Per esempio, se il parametro che controlla la transizione è il campo magnetico, la derivata dell'energia libera rispetto al campo magnetico è la magnetizzazione del sistema. Nella fase ferromagnetica il comportamento della magnetizzazione come funzione del campo magnetico è riportato schematicamente nella fig. 3B: un campo magnetico esterno ararbitrariamente piccolo è sufficiente per stabilire in quale direzione la magnetizzazione debba puntare. In questo caso la transizione è del prim'ordine.
3. Diagramma delle fasi
Abbiamo visto nei capitoli precedenti che lo stesso sistema può trovarsi in diverse fasi e che i parametri che controllano le transizioni sono molto spesso più di uno. Può essere conveniente descrivere la struttura delle fasi mediante un diagramma (bidimensionale) detto ‛diagramma delle fasi': in genere si riporta in ascissa la temperatura e in ordinata un parametro di controllo rilevante (per esempio la pressione o il campo magnetico). Per ciascuna fase possibile del sistema viene indicata nel diagramma la regione corrispondente del parametro di controllo.
Vediamo alcuni esempi caratteristici.
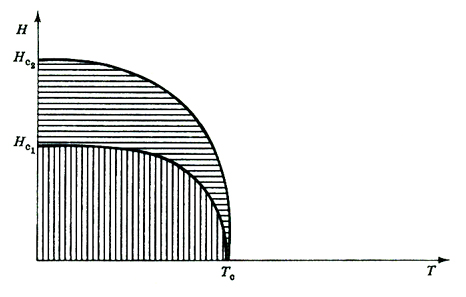
1. Nella fig. 4 è rappresentato il diagramma delle fasi di un materiale che diventa superconduttore di seconda specie a basse temperature nel piano temperatura-campo magnetico. Le linee di transizione di fase separano fasi differenti: la fase normale dalla fase mista e la fase mista dalla fase superconduttrice.
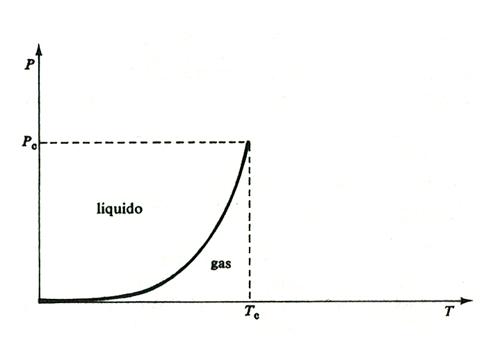
2. Nella fig. 5 vediamo il diagramma delle fasi di una sostanza pura (per esempio l'acqua) nel piano temperatura-pressione, per quanto riguarda la transizione liquido-gas.
Come abbiamo anticipato nel cap. 1, la regione del diagramma occupata dalla fase fluida è connessa: la linea della transizione gas-liquido termina (nel cosiddetto punto critico) ed è possibile passare dalla ‛fase' liquida alla ‛fase' gassosa senza incontrare una transizione di fase, a patto di operare a pressioni e a temperature superiori a quelle del punto critico (circa 200 atmosfere e 400 °C per l'acqua).
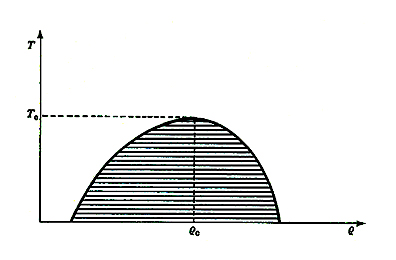
Lo stesso diagramma delle fasi può essere rappresentato nel piano densità-temperatura (v. fig. 6). Nella zona bianca il sistema si trova in una fase pura, ovvero spazialmente omogenea, nella zona tratteggiata avviene una separazione delle fasi: per esempio, se la densità media del fluido è intermedia tra quella del gas e quella del liquido, parte del sistema sarà un gas e parte sarà un liquido.
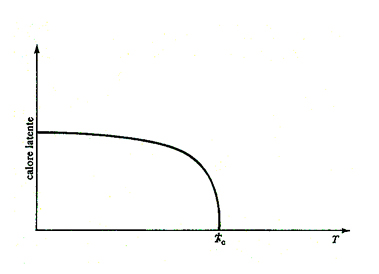
Il comportamento del calore latente nella transizione gas-liquido è illustrato nella fig. 7. Il calore latente si annulla quando la pressione raggiunge il valore del punto critico, che è quindi un punto di transizione del second'ordine. La linea delle transizioni gas-liquido è composta da transizioni di fase del prim'ordine e termina con una transizione di fase del second'ordine (in moltissimi casi una transizione di fase del second'ordine è il punto terminale di una linea di transizioni di fase del prim'ordine).
3. Nella fig. 8 vediamo il diagramma delle fasi di un tipico ferromagnete. Se variamo la temperatura a campo magnetico nullo, incontriamo una transizione di fase del second'ordine alla temperatura critica. Per temperature più piccole della temperatura critica, quando il campo magnetico passa da positivo a negativo, il sistema subisce una transizione di fase del prim'ordine con cambiamento di segno della magnetizzazione. Anche in questo caso la linea delle transizioni di fase del prim'ordine termina in una transizione del second'ordine.
4. Transizioni di fase del prim'ordine e stati metastabili
Una delle caratteristiche salienti delle transizioni di fase del prim'ordine è l'esistenza di stati metastabili: un sistema si trova in uno stato metastabile se può rimanere in questo stato per un periodo di tempo estremamente grande in assenza di perturbazioni esterne; tuttavia (a differenza di uno stato veramente stabile) una piccola, ma appropriata, perturbazione è sufficiente a scatenare il passaggio dallo stato metastabile a uno stato più stabile.
L'esempio probabilmente più noto di stato metastabile è una miscela di ossigeno (O2) e di idrogeno (H2) a temperatura ambiente. La miscela è esplosiva e basta una scintilla o una piccola fiamma per farla esplodere; il prodotto di questa reazione violenta è acqua (H2O).
Un esempio meno pericoloso è costituito dall'acqua soprafusa. L'acqua estremamente pura, se raffreddata lentamente, rimane liquida anche a temperature ben al di sotto di O °C. La presenza di qualsiasi impurità, o di granelli di ghiaccio, innesca un processo di cristallizzazione a catena. Lavorando con cura è possibile raggiungere temperature di −25 °C mantenendo l'acqua liquida.
Lo stato metastabile inverso (ghiaccio surriscaldato) è estremamente difficile da ottenere, in quanto sulla superficie del ghiaccio c'è sempre un sottile strato di liquido che innesca il processo di fusione. Per quanto numerose siano le precauzioni prese, un pezzo di ghiaccio fonde, a partire dalla superficie, appena portato a una temperatura superiore a O °C.
Del ghiaccio surriscaldato è stato tuttavia ottenuto recentemente riscaldando un cristallo di ghiaccio mediante due raggi laser. Solo nella zona all'incrocio fra i due raggi laser la temperatura del ghiaccio supera O °C. In questo modo la regione a temperatura maggiore di zero risulta circondata dal ghiaccio a temperatura più bassa e non dallo strato d'acqua, sicché si è riusciti a portare il ghiaccio diversi gradi sopra lo zero senza che fondesse.
La perturbazione che fa passare dallo stato metastabile a uno stato stabile può anche non essere esterna, ma derivare da una fluttuazione termodinamica.
Il meccanismo microscopico alla base della metastabilità è abbastanza semplice. Prendiamo in considerazione per chiarezza il caso dell'acqua soprafusa. Nella fase liquida le molecole dell'acqua sono disordinate; quando la temperatura scende al di sotto di O °C, dal punto di vista termodinamico per le molecole sarebbe conveniente assumere una configurazione ordinata, cioè disporsi in un cristallo di ghiaccio. Le molecole non possono sapere che cosa sia conveniente per loro senza aver fatto prima la prova: in altri termini è necessario che si formi un primo nucleo di cristallo di ghiaccio e in questo modo le molecole, attaccandosi a questo cristallo e staccandosene, possono verificare quale delle due situazioni (stare disordinate nel liquido o ordinate nel ghiaccio) sia per loro più conveniente.
Un cristallo di ghiaccio iniziale è essenziale per far partire il processo di cristallizzazione. Impurezze presenti nell'acqua (tipicamente granelli microscopici di polvere) favoriscono la transizione, in quanto sulla loro superficie si può formare facilmente un primo strato di ghiaccio che dà inizio alla cristallizzazione.
Se l'acqua non contiene impurezze, questo meccanismo non può essere operativo e in prima approssimazione il liquido non congela. Può tuttavia capitare che alcune molecole, muovendosi a caso, formino un minicristallo di ghiaccio che serve da innesco per la transizione di fase; si tratta di una eventualità molto rara e bisogna aspettare molto tempo perché si verifichi; per questo motivo la vita media dello stato metastabile è estremamente elevata (in moltissimi casi praticamente infinita).
Una teoria microscopica più dettagliata mostra che il raggio del cristallo di ghiaccio iniziale deve essere (vicino alla temperatura di transizione Tc) proporzionale a (Tc − T)-1. Più il raggio è grande, più è improbabile che il cristallo si formi spontaneamente; con considerazioni di questo tipo si può mostrare (v. Langer, 1967) che la vita media di uno stato metastabile è proporzionale a
exp [C/(T − Tc)2], (1)
in cui C è una costante positiva.
Fenomeni di metastabilità sono molto comuni nei materiali ferromagnetici. Consideriamo per semplicità un materiale in cui la magnetizzazione possa puntare in due sole direzioni, l'una l'opposta dell'altra (v. Ising, 1925).
Come abbiamo già visto, sotto la temperatura critica basta un campo magnetico estremamente piccolo per creare una magnetizzazione spontanea nella direzione del campo magnetico. Questo è certamente vero se il sistema è preparato a una temperatura più alta della temperatura critica e poi viene raffreddato in presenza di un campo magnetico. Se il campo magnetico viene successivamente rimosso, il sistema rimane magnetizzato nella stessa direzione. In questa situazione un ulteriore debole campo magnetico, nella direzione opposta a quella precedente, non è sufficiente a ribaltare la magnetizzazione e il sistema rimane in uno stato metastabile. Solo dopo un tempo estremamente grande il sistema riesce a cambiare il segno della magnetizzazione spontanea e a passare nello stato stabile.
Nei magneti reali la situazione è molto più complicata, a causa dell'esistenza di forze magnetiche a lungo raggio d'azione (forze dipolari), che tendono a ridurre la magnetizzazione totale del sistema. Il compromesso fra l'interazione fra gli spins vicini, che tende a ordinare localmente il sistema, e le forze dipolari, che tendono a disordinare il sistema su grande scala, viene raggiunto con la formazione di domini magnetici molto più grandi della scala molecolare (di qualche decina di μm di diametro), separati da regioni sottili qualche centinaio di Å (pareti di Bloch), in cui la magnetizzazione non ha un segno definito. Dentro ciascun dominio gli spins sono orientati nella stessa direzione, mentre i vari domini sono orientati in direzioni diverse (v. Kittel, 1966).
Un campo magnetico esterno positivo ha l'effetto di aumentare la grandezza dei domini magnetici con magnetizzazione positiva a spese degli altri domini magnetici. Il moto delle pareti magnetiche, quando viene aggiunto un campo esterno, è assai complicato; le impurezze presenti nel materiale e i difetti di cristallizzazione tendono a inchiodare le pareti magnetiche in certe posizioni privilegiate.
Sperimentalmente si osserva che queste pareti si muovono a scatti: al variare del campo magnetico la parete si stacca da una o più impurezze a cui era inchiodata e si muove finché non arriva ad agganciarsi a un altro appiglio. Il sistema delle pareti magnetiche sta quasi sempre in uno stato metastabile, abbastanza distante dallo stato di equilibrio termodinamico. Il numero di stati metastabili possibili è estremamente elevato e la configurazione in cui si trova un magnete permanente dipende dalla sua storia magnetica precedente; infatti, se un pezzo di ferro non magnetizzato viene sottoposto momentaneamente a un campo magnetico esterno, esso rimane magnetizzato in maniera quasi permanente (isteresi magnetica) e l'ammontare della magnetizzazione permanente dipende dal campo magnetico applicato. Successivamente, col passare degli anni (o dei giorni o dei secoli, a seconda del tipo di materiale) la magnetizzazione diminuisce e il ferro si smagnetizza.
5. Ordine e disordine
Molto spesso è possibile caratterizzare una fase della materia mediante proprietà di ordine o disordine (v. Landau e Lifschitz, 1971). Anche in questo caso conviene fare degli esempi.
A. In un solido amorfo gli atomi sono affastellati l'uno contro l'altro, in disordine; al contrario in un cristallo gli atomi sono ben ordinati e formano un reticolo regolare. Quando l'amorfo diventa un cristallo, gli atomi si dispongono in maniera più ordinata di prima: abbiamo quindi una transizione da una fase disordinata a una fase ordinata (in breve una transizione disordine-ordine).
Il numero di reticoli regolari è estremamente elevato e a volte nella cristallizzazione di uno stesso sistema fisico gli atomi si dispongono secondo due diversi reticoli regolari, per esempio cubico a facce centrate e cubico semplice (v. Kittel, 1966). In questo caso possiamo avere una transizione di fase in cui, al variare dei parametri fisici, si passa da una struttura ordinata a un'altra struttura ordinata.
B. Secondo un modello molto semplice (ma molto istruttivo) un materiale ferromagnetico consiste di magnetini elementari (spins) che costituiscono la sorgente del campo magnetico e che possono essere orientati in varie direzioni (modello di Heisenberg); in un'ulteriore schematizzazione (che corrisponde a quello che in realtà accade in alcuni materiali) gli spins possono puntare in due sole direzioni, chiamate convenzionalmente ‛alto' e ‛basso'. L'interazione tra gli spins è tale da tendere a orientarli tutti nella stessa direzione (modello di Ising).
Dato che l'agitazione termica ha un effetto opposto, tende cioè a disordinare gli spins, a bassa temperatura gli spins non sono disturbati dal rumore termico e riescono ad allinearsi gli uni con gli altri, mentre a temperatura più alta del punto di Curie (v. cap. 1) non riescono a ordinarsi e puntano in varie direzioni. Nella fase paramagnetica ad alta temperatura il sistema è disordinato, mentre nella fase magnetica a bassa temperatura il sistema è ordinato.
Il sistema può ordinarsi in vari modi; nel caso del modello di Ising abbiamo solo due possibilità: la maggioranza degli spins può puntare o verso l'alto o verso il basso. Mentre un campo magnetico esterno tende a favorire uno dei due casi, in assenza di un campo magnetico esterno le due possibilità sono equivalenti ed entrambe possono verificarsi.
In assenza di campo magnetico l'operazione di cambiare l'orientamento di tutti gli spins del sistema non modifica l'energia del sistema (una trasformazione che non cambia l'energia è una simmetria del sistema). Mentre ad alta temperatura il sistema può stare in un solo stato (50% degli spins in alto, 50% degli spins in basso, distribuiti in maniera casuale), che rimane lo stesso quando si invertono tutti gli spins, a bassa temperatura il sistema può stare in due stati possibili, che sono trasformati l'uno nell'altro dall'operazione di invertire gli spins.
In quest'ultimo caso, quando cioè esiste una simmetria, ma il sistema può stare in uno stato non invariante sotto l'azione della simmetria (l'insieme degli stati del sistema è necessariamente invariante sotto l'azione della simmetria), si dice che la simmetria è spontaneamente rotta, altrimenti la simmetria è esatta. La transizione di fase magnetica può essere vista (come d'altronde tutte le transizioni ordine-disordine) come la transizione tra una fase in cui una simmetria è esatta e una fase in cui la stessa simmetria è rotta.
C. Anche la transizione conduttore-superconduttore è una transizione ordine-disordine; tuttavia in questo caso è molto meno intuitivo capire che cosa si ordini: la meccanica quantistica gioca infatti un ruolo cruciale nei fenomeni di superconduttività e di superfluidità (v. meccanica statistica, cap. 5).
Allo scopo di quantificare l'ordine presente in un sistema è conveniente introdurre un parametro d'ordine: per esempio, nel caso di un materiale ferromagnetico (modello di Ising), il parametro d'ordine p del sistema è dato dalla percentuale di spins in alto meno la percentuale di spins in basso. Nella fase a simmetria esatta il parametro d'ordine è zero, mentre nella fase a simmetria rotta il parametro d'ordine può assumere due valori differenti, l'uno opposto dell'altro. La magnetizzazione spontanea del sistema è proporzionale al parametro d'ordine, il coefficiente di proporzionalità essendo dipendente dal sistema. Nel limite di temperatura zero il parametro d'ordine è 1 o −1 e la magnetizzazione spontanea assume il valore massimo possi bile.
In maniera simile è possibile definire un parametro d'ordine per le altre transizioni ordine-disordine; nel caso del modello di Heisenberg il parametro d'ordine è un vettore che punta nella direzione della maggioranza degli spins. Molto spesso è utile introdurre un parametro d'ordine locale (funzione della posizione x), uguale alla percentuale di spins in alto meno la percentuale di spins in basso, considerando solo gli spins nelle immediate vicinanze del punto x.
Le transizioni di fase ordine-disordine si possono classificare in base al tipo di parametro d'ordine e alla simmetria che si rompe spontaneamente alla transizione di fase (normalmente la fase ordinata è quella a temperatura più bassa); la teoria dei gruppi fornisce uno strumento concettuale adeguato.
In casi più complicati l'introduzione di un parametro d'ordine deve essere fatta con notevole cura. Per esempio, in alcuni cristalli liquidi le molecole sono come dei bastoncini oblunghi, che a basse temperature tendono a mettersi tutti paralleli: il parametro d'ordine è la direzione in cui punta la maggior parte delle molecole, ma non si tratta di un vettore in senso stretto, in quanto due versi opposti fra di loro corrispondono allo stesso stato.
L'uso degli strumenti più moderni della teoria dei gruppi (ad esempio il gruppo di omotopia, v. algebra) diventa essenziale nello studio di problemi più complessi come la classificazione dei difetti nella fase ordinata.
Molti dei progressi di questi ultimi anni nello studio delle transizioni di fase sono stati ottenuti utilizzando in maniera essenziale il concetto di parametro d'ordine. Non è probabilmente un caso che al momento attuale la nostra comprensione della transizione liquido-amorfo (per esempio nel vetro) sia molto scarsa: in questo caso i due sistemi sono entrambi disordinati e la transizione non può essere caratterizzata dalla presenza di un parametro d'ordine facilmente identificabile.
6. Teoria microscopica e termodinamica delle transizioni di fase
Nei capitoli precedenti abbiamo visto le caratteristiche essenziali delle transizioni di fase; rimane aperto il problema di determinare teoricamente per una data sostanza il diagramma delle fasi, sia nei suoi aspetti qualitativi che nei suoi aspetti quantitativi. Se si esclude un numero estremamente ristretto di casi fortunati (alcuni sistemi bidimensionali: v. Mc Coy e Wu, 1978), calcoli ‛quantitativi' sono possibili solo in maniera approssimata e per molti sistemi alcuni aspetti ‛qualitativi' non sono stati ancora ben compresi (per esempio nella transizione vetrosa, ovvero liquido-amorfo).
In generale, più l'approssimazione richiesta deve essere precisa, più i calcoli necessari devono essere complicati (v. Domb e Green, 1972-1980). In questo capitolo discuteremo una delle approssimazioni più semplici, che rende ben conto del comportamento qualitativo e quantitativo delle più comuni transizioni di fase del prim'ordine. Nel capitolo successivo vedremo che nuove schematizzazioni teoriche sono necessarie per una comprensione qualitativamente accurata delle transizioni di fase del second'ordine.
L'idea alla base del metodo è molto semplice. Dalla termodinamica elementare sappiamo che a ogni stato del sistema possiamo associare l'energia libera (v. Ma, 1985)
F = U − TS = U − kTS′, (2)
dove U è l'energia interna, T è la temperatura ed S è l'usuale entropia termodinamica; S' indica invece l'entropia microscopica, ovvero il logaritmo del numero degli stati microscopici su cui si muove il sistema. La relazione fra le due entropie è ben nota: S = kS′; k indica, come d'abitudine, la costante di Boltzmann (circa 1,38 • 10 -16 erg/K).
Il secondo principio della termodinamica implica che, se viene fornita (o sottratta) energia meccanica a un sistema a contatto con una sorgente a temperatura costante, l'energia libera del sistema può solamente diminuire: quando l'energia libera assume il suo valore minimo, il sistema raggiunge l'equilibrio termodinamico. Il passo cruciale per determinare la struttura del diagramma delle fasi consiste nell'identificare uno o più parametri fisici che caratterizzino lo stato del sistema, e nel calcolare l'energia libera come funzione di questi parametri. I valori che i parametri assumono all'equilibrio vengono determinati cercando il minimo dell'energia libera.
Nel caso dei sistemi magnetici il parametro più naturale è la densità di magnetizzazione (o equivalentemente il parametro d'ordine del cap. 5), mentre per la transizione gas-liquido è la densità del fluido.
Consideriamo per primo un sistema magnetico di Ising. La densità di magnetizzazione m è proporzionale al parametro d'ordine p (definito nel cap. 5). Nell'ipotesi che si possano trascurare le fluttuazioni del valore del parametro d'ordine da punto a punto (questa ipotesi fallisce clamorosamente vicino alle transizioni di fase del second'ordine) un calcolo dettagliato porta alla seguente espressione per l'energia libera per un sistema di N spins:
Formula (3)
dove In indica il logaritmo naturale, T è la temperatura, h è il campo magnetico, misurato in unità opportune, e J è una costante che dipende dal materiale ed è proporzionale all'accoppiamento tra i vari spins.
Condizione necessaria, ma non sufficiente, affinché l'energia libera per spin (f(p) F(p)/N) sia minima, è che l'equazione
∂f/∂p = 0 (4)
sia soddisfatta. Tenendo conto dell'espressione di F(p) data ‛all'equazione (3), l'equazione (4) si riduce a
p = th(βJp + βh), (5)
dove th indica la tangente iperbolica e β è un'abbreviazione per l/(kT).
Calcoli abbastanza semplici fanno vedere che la temperatura di transizione ferromagnetica (al di sotto della quale f(p) ha due minimi simmetrici a p diverso da zero) è data da
Tc = k/J. (6)
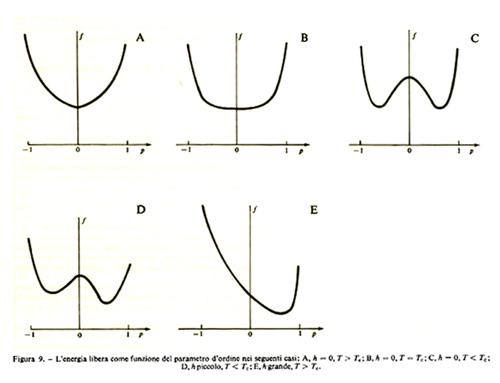
Nella fig. 9, A-E sono indicati i vari comportamenti possibili della funzione f(p) al variare della temperatura e del campo magnetico. A seconda dei casi possiamo avere: a) una sola fase stabile (fig. 9, A, B ed E); b) due fasi con la stessa energia libera; le due fasi sono entrambe stabili (fig. 9C); c) due fasi con energia libera differente; il minimo assoluto corrisponde alla fase stabile mentre il minimo locale corrisponde alla fase metastabile (fig. 9D).
Nei casi 9C e 9D l'equazione (4) ammette anche una terza soluzione, che non è fisicamente rilevante in quanto corrisponde a un massimo, non a un minimo dell'energia libera.
Nella fig. 10 si vedono i grafici dell'energia libera e della magnetizzazione in funzione del campo magnetico.
Risultati simili possono ottenersi per la transizione gas-liquido (v. Baracca, 1980). In questo caso la densità e del fluido gioca il ruolo del parametro d'ordine p. La trattazione più semplice di questa transizione risale a van der Waals. Sono necessari due ingredienti: una forza attrattiva fra le molecole, quando esse sono a grande distanza, per favorire energeticamente la fase liquida, e una forza repulsiva a corta distanza, per impedire alle molecole di sovrapporsi le une alle altre.
Dopo aver fatto alcune semplificazioni sulla natura di queste forze e aver trascurato gli effetti delle fluttuazioni (come nel caso precedente), si trova che la densità e soddisfa la seguente equazione:
(P + aρ2) (ρ-1 − b) = RT, (7)
dove P è la pressione, T è la temperatura, a e b sono due costanti dipendenti dal materiale (proporzionali rispettivamente alla forza attrattiva e alla forza repulsiva) ed R è la costante dei gas.
Utilizzando l'equazione (7) ed eliminando le regioni metastabili e instabili si trova un diagramma delle fasi abbastanza simile a quello delle figg. 5 e 6. Il punto critico, dove termina la linea di transizione di fase del prim'ordine, è dato dai seguenti valori:
PC = a/27b2 ρC = 1/(3b) TC 8a/27Rb. (8)
I risultati che si possono ottenere mediante le equazioni (5) e (7) sono in buon accordo con i dati sperimentali, se non si è troppo vicini al punto di transizione di fase del second'ordine, nel qual caso la trattazione deve essere modificata, come vedremo nel prossimo capitolo.
7. Transizioni di fase del second'ordine
a) Esponenti critici
Il calore specifico di un sistema che subisce una transizione del second'ordine, se calcolato con il metodo del capitolo precedente, risulta essere una funzione discontinua della temperatura; l'approssimazione principale consiste nel trascurare le fluttuazioni locali del parametro d'ordine (sia esso p o ρ) attorno alla posizione di equilibrio. Se si tiene conto perturbativamente di dette fluttuazioni (ovvero se si fa l'ipotesi che il loro effetto sia piccolo), si trova che il calore specifico è dato da
C(T) = a ∣ T − TC ∣-α + b α = 1/2, (9)
a e b essendo delle costanti dipendenti dal materiale.
Il calore specifico diverge alla temperatura critica, mentre nell'approssimazione del capitolo precedente rimane finito alla temperatura critica. Non è sostenibile l'ipotesi che l'effetto delle fluttuazioni rimanga piccolo vicino alla temperatura critica.
L'origine di questo insuccesso può essere facilmente compresa se si considera la suscettività magnetica χ, ovvero la derivata della magnetizzazione rispetto al campo magnetico:
χ v= ∂M/∂H = (∂2F/∂M2)-1. (10)
Come si può dedurre dalla fig. 10, χ diverge alla temperatura critica; un calcolo più dettagliato mostra che vicino alla temperatura critica si ha
x ≈ ∣ T − TC ∣-γ γ = 1. (11)
La divergenza di χ alla temperatura critica non deve stupire: per temperature più basse della temperatura critica una magnetizzazione spontanea è presente anche in assenza di campo magnetico; alla temperatura critica un campo magnetico relativamente piccolo produce una magnetizzazione relativamente grande. Un calcolo esplicito mostra che alla temperatura critica si ha
M ≈ H1/δ (H > 0) δ = 3. (12)
Questi risultati si ottengono dalle formule del capitolo precedente che sono state derivate trascurando l'effetto delle fluttuazioni. Una stima delle fluttuazioni può essere ottenuta utilizzando il cosiddetto teorema di fiuttuazione-dissipazione (v. termodinamica irreversibile e sinergetica): nel caso del modello di Ising, dove la magnetizzazione può puntare in una sola direzione, si trova che, a temperature maggiori della temperatura critica e in assenza di un campo magnetico esterno, si ha
Nχ = β < M2 >, (13)
dove N è il numero totale di spins, β è come il solito 1/(kT) e il simbolo < > denota il valore d'aspettazione termodinamico.
Dato che in questo caso la magnetizzazione è zero (< M > = 0), <M2 > misura le liuttuazioni della magnetizzazione totale: esse divergono alla temperatura critica.
Un calcolo più dettagliato mostra che per temperature leggermente superiori alla temperatura critica il sistema si può decomporre in regioni in cui gli spins sono localmente ordinati e puntano nella stessa direzione in ciascuna regione; il raggio medio di queste regioni (ovvero la lunghezza di correlazione, che comunemente si indica con ξ diverge alla temperatura critica:
ξ ≈ ∣ T − TC ∣-ν ν = 1/2. (14)
Corrispondentemente la funzione di correlazione del parametro d'ordine, g(r) ~ <;M(0)M(r)>, tende a zero per r → ∞ come
Formula (15)
Dato che l'orientazione di una regione non dipende dalle orientazioni delle regioni vicine, la magnetizzazione totale rimane nulla. Quando si raggiunge la temperatura critica, ξ diventa infinito: una singola regione, magnetizzata in maniera coerente, ricopre tutto il sistema e si sviluppa una magnetizzazione spontanea diversa da zero.
In conclusione l'approssimazione di trascurare le fluttuazioni non è consistente, in quanto predice l'esistenza di fluttuazioni non trascurabili. Il problema di trovare un'approssimazione consistente ha portato, molto recentemente, a una nuova teoria e l'analisi dei dati sperimentali ha fornito suggerimenti importanti.
Il primo confronto dei risultati delle innumerevoli esperienze fatte su sistemi che subiscono transizioni di fase del second'ordine mostra che le equazioni (9)-(15) sono qualitativamente corrette, tuttavia i vari parametri α, γ, δ, ν ed η (che vengono chiamati esponenti critici) assumono valori diversi da quelli indicati nelle formule (un altro esponente critico molto importante è β, da non confondersi con 1/(kT), definito da M ≈ (TC - T)β in assenza di campo magnetico esterno).
Il risultato che più sconcertò i fisici dei primi anni sessanta era che, al cambiare del materiale, la temperatura critica e le varie proprietà del sistema cambiavano, ma gli esponenti critici rimanevano gli stessi per tutti i materiali ferromagnetici che potevano essere ben descritti dalla schematizzazione di Ising. Nei materiali ferromagnetici in cui la magnetizzazione poteva puntare in tutte le direzioni (modello di Heisenberg) gli esponenti critici assumevano valori diversi, anche qui indipendenti dal materiale.
Le varie transizioni del second'ordine si potevano dividere in alcune classi di universalità, ciascuna delle quali caratterizzata dal tipo di parametro d'ordine (per esempio un numero o un vettore) e dal fatto che gli esponenti critici vi assumevano gli stessi valori. In particolare gli esponenti rilevanti per il punto critico della transizione gas-liquido erano gli stessi (mutatis mutandis) degli esponenti per la transizione ferromagnetica di Ising: in entrambi i casi il parametro d'ordine era uno scalare.
Gli esponenti critici sono grandezze universali, in quanto non dipendono dai dettagli dell'interazione (ovviamente gli esponenti critici di sistemi bidimensionali sono differenti da quelli degli equivalenti sistemi tridimensionali: la dimensione D dello spazio è un parametro rilevante come lo è, del resto, anche il tipo di parametro d'ordine).
La misura sperimentale degli esponenti critici è meno semplice di quanto si possa credere; le equazioni (9) e (11)-(15) danno risultati affidabili solo molto vicino alla temperatura critica, altrimenti si rendono necessarie correzioni importanti: per esempio, l'equazione (9) diventa
C(T) = 2a ∣ T − TC ∣-α (1 + A ∣ T − TC ∣ων) + b, (16)
dove ω è un nuovo esponente critico (anch'esso universale).
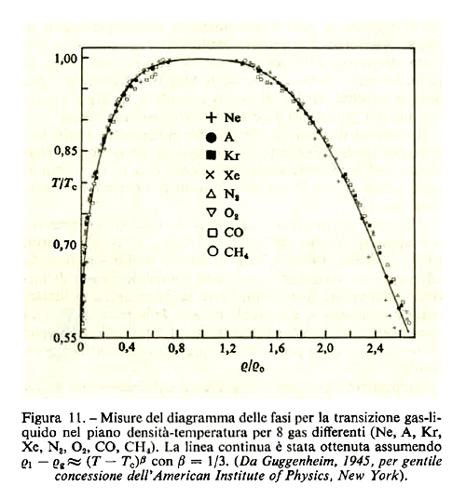
Al contrario la costante A, che parametrizza le deviazioni da una semplice legge di potenza, dipende dalla sostanza: sistemi diversi si comporteranno in modo simile molto vicino alla temperatura critica, ma non appena ci allontaniamo dalla temperatura critica essi si comporteranno in modo diverso (v., per esempio, la fig. 11, dove sono mostrati i dati sperimentali per la curva di coesistenza per varie sostanze vicino al punto critico della transizione gas-liquido).
La difficoltà principale consiste nel compiere misure accurate molto vicino alla temperatura critica; i risultati migliori sono stati ottenuti per la transizione fluido-superfluido dell'elio (il cosiddetto ‛punto λ').
A pressione ambiente la transizione avviene a circa 2,2 K. L'esperienza consiste nel misurare il calore specifico del sistema a diverse temperature e a diverse pressioni: usando speciali accorgimenti si è riusciti a regolare la temperatura con una precisione di 10-7K (v. Ahlers, 1973). Al variare della pressione esterna si è verificato che la temperatura critica e le varie costanti cambiavano sensibilmente, mentre i valori degli esponenti critici restavano gli stessi con grande precisione.
b) Il gruppo di rinormalizzazione
La teoria che permette di spiegare i fenomeni che avvengono vicino a una transizione del second'ordine porta il nome di ‛gruppo di rinormalizzazione' ed è stata sviluppata, a cavallo fra gli anni sessanta e settanta, inizialmente da Kadanoff (v. Kadanoff e altri, 1967) e successivamente da Wilson (v. Wilson, 1971; v. Wilson e Kogut, 1974), il quale, per il suo contributo, ha ricevuto nel 1982 il premio Nobel. Il nome abbastanza strano è dovuto al fatto che una tecnica simile era stata introdotta nella teoria delle particelle elementari (v. Stueckelberg e Peterson, 1953; v. Gell-Mann e Low, 1954), nel cui contesto il nome di ‛gruppo di rinormalizzazione' era più giustificato.
La difficoltà principale, nel trattare con metodi convenzionali le transizioni di fase di seconda specie, è dovuta (nel caso dei sistemi magnetici) al formarsi di regioni molto grandi nelle quali gli spins sono prevalentemente orientati nella stessa direzione. Un'analisi più precisa rivela che ciascuna regione si può decomporre in sottoregioni con le stesse caratteristiche: ognuna delle sottoregioni può a sua volta decomporsi in regioni ancora più piccole, ecc.; la suddivisione si arresta quando il raggio della regione più piccola diventa uguale al passo reticolare. Il raggio della regione più grande (ξ) diverge alla temperatura critica.
Il numero di gradi di libertà che giocano un ruolo importante tende all'infinito al punto di transizione e il problema non è affrontabile direttamente con le approssimazioni usuali, in cui il numero di gradi di libertà deve rimanere finito.
Il gruppo di rinormalizzazione ci fornisce uno strumento per aggirare questa difficoltà (v. Amit, 1978; v. Wilson, 1979; v. Parisi, 1986). L'idea di base è molto semplice da afferrare una volta che siano state comprese alcune definizioni preliminari (per semplificare la discussione ci limiteremo a considerare solamente il caso della transizione ferromagnetica nella schematizzazione del modello di Ising; l'estensione al caso generale non presenta difficoltà di principio).
Supponiamo per semplicità che gli spins risiedano su un reticolo regolare cubico di passo a. Possiamo introdurre un reticolo di passo L (con La intero) sovrapposto al precedente; il parametro d'ordine locale relativo alla scala L (PL) è definito sul nuovo reticolo ed è proporzionale alla somma di tutti gli spins in un cubo di lato L, la costante di proporzionalità essendo fissata dalla condizione
<pL2 > = 1. (17)
Per L = a, pL coincide con il singolo spins e, per L che tende all'infinito, pL è proporzionale all'usuale parametro d'ordine globale.
La definizione di parametro d'ordine locale relativo alla scala L non è univoca; molte altre definizioni (fisicamente equivalenti) sono possibili: per esempio (se consideriamo valori di L tali che La sia sempre un numero dispari) pL è uguale a 1 se la somma di tutti gli spins del cubo è positiva, altrimenti pL è uguale a − 1.
Nella fase di alta temperatura, p∞ (ovvero pL, per un valore di L molto grande rispetto al passo reticolare) è la somma di un numero infinito di variabili indipendenti e quindi, per il teorema del limite centrale, la sua distribuzione di probabilità è gaussiana (v. probabilità); infatti, non essendoci magnetizzazione spontanea, gli spins che si trovano a distanza molto maggiore di ξ non sono praticamente correlati. Nella fase a bassa temperatura, p∞ assume solo il valore 1 (oppure − 1, a seconda del segno della magnetizzazione spontanea), in quanto non ci sono fluttuazioni attorno al valore medio della magnetizzazione (se esso è diverso da zero) su una regione macroscopica.
Se per L abbastanza grande la distribuzione di probabilità delle variabili pL è la stessa delle variabili p2L, il sistema si dice ‛invariante per trasformazioni di scala' nella regione delle grandi distanze: la trasformazione che fa passare dalle variabili pL alle variabili P2L si chiama ‛trasformazione di scala'.
Normalmente viene fatta l'ipotesi che il sistema sia sempre invariante per trasformazioni di scala. Allo scopo di capire il significato di questa affermazione è utile fare un esempio esplicito.
Consideriamo un sistema di Ising bidimensionale (di superficie infinita), i cui spins positivi appaiano come macchioline nere e i cui spins negativi come macchioline bianche. Supponiamo di osservare il sistema su uno schermo televisivo con la telecamera posta a distanza variabile dal sistema. Quando la distanza d è piccola, possiamo vedere i singoli spins, quando la distanza è grande, a causa della risoluzione dello schermo televisivo possiamo vedere solo il contributo medio di molti spins: la dimensione della regione minima che possiamo vedere distintamente aumenta linearmente con la distanza della telecamera dal sistema; le informazioni sulla struttura fine del sistema vengono perse e l'immagine che appare sullo schermo dipende solo dalle variabili pL, con L proporzionale a d. All'aumentare della distanza può essere necessario aumentare il contrasto, per evitare una distribuzione uniformemente grigia; quest'ultima operazione corrisponde a imporre l'equazione (17).
Nella regione ad alta temperatura, per d molto grande, l'immagine televisiva è priva di interesse ed è molto simile a quella di un televisore che riceve solo rumore: ogni punto e, indipendentemente dai punti vicini, bianco o nero. Al contrario, nella regione a bassa temperatura, non appena d è sufficientemente grande, lo schermo sarà tutto bianco o tutto nero, a seconda che la magnetizzazione spontanea sia negativa o positiva.
In questa similitudine l'ipotesi d'invarianza di scala implica che, osservando l'immagine televisiva per d grande, non è praticamente possibile determinare il valore di d; più precisamente le immagini prese da una distanza d e quelle prese da una distanza 2d diventano sempre più simili quando d tende all'infinito.
Le considerazioni che abbiamo fatto implicano che il sistema è invariante per trasformazioni di scala, tranne che alla temperatura critica e a campo magnetico nullo. L'invarianza di scala del sistema anche al punto critico è una delle ipotesi che sta alla base del metodo del gruppo di rinormalizzazione.
Esattamente alla temperatura di transizione anche per d estremamente grande dovremmo vedere delle regioni più o meno chiare, che contengono delle regioni più piccole dai toni più forti. Quando la distanza aumenta, le regioni più grandi diventano più piccole e nuove regioni vengono inglobate nell'immagine televisiva.
Se non siamo esattamente alla temperatura critica ma a una temperatura lievemente superiore, quando la risoluzione diventa più piccola della lunghezza di correlazione, torniamo a vedere lo schermo punteggiato casualmente, tipico della regione ad alta temperatura. Parallelamente, a temperature leggermente più basse della temperatura critica, solo quando d diventa molto grande lo schermo diventa uniformemente bianco o nero. Solo per d estremamente grande il passaggio tra la regione a bassa temperatura e quella ad alta temperatura avviene bruscamente, mentre, per d non tanto grandi, le immagini prese sotto e sopra la temperatura critica sono molto simili.
Non ci resta altro che formalizzare matematicamente queste idee intuitive (che sono peraltro confermate da simulazioni numeriche: v. fig. 12). Indichiamo con pL la distribuzione di probabilità delle variabili pL; dato che le variabili P2L sono delle funzioni delle variabili pL, la loro distribuzione di probabilità P2L può essere calcolata a partire dalla distribuzione di probabilità PL; in altri termini si ha
P2L = R (PL), (18)
dove R è un operatore non lineare che può essere più o meno complicato; la trasformazione (18) è una trasformazione di scala e l'operatore R è l'operatore di base del gruppo di rinormalizzazione; infatti gli operatori Rn, ottenuti applicando R n volte (P2nL = Rn(PL)), formano un gruppo (o meglio un semigruppo) che viene chiamato ‛gruppo di rinormalizzazione'.
L'ipotesi di invarianza di scala implica che la distribuzione di probabilità per le variabili pL esista nel limite in cui L tende all'infinito; essa deve soddisfare l'equazione non lineare
P∞ = R sx(P∞). (19)
Trovare tutte le distribuzioni di probabilità possibili per le variabili pL per alti valori di L corrisponde a risolvere l'equazione (19).
In generale le distribuzioni di probabilità di un sistema possono dipendere da un numero estremamente elevato di parametri e l'operatore R agisce su uno spazio con un numero infinito di parametri. A questo punto è necessario fare l'ipotesi che sia possibile approssimare la vera distribuzione di probabilità P∞ con delle distribuzioni di probabilità relativamente semplici, che dipendono da un numero piccolo di parametri. Se per fortunata combinazione siamo anche in grado di valutare approssimativamente l'azione dell'operatore R su tali distribuzioni, possiamo trasformare le equazioni (19) in equazioni esplicite per un numero finito di variabili.
A scopo illustrativo supponiamo che le distribuzioni di probabilità P2nL dipendano solamente da un parametro Kn, che indichi quanto è forte la correlazione tra i valori del parametro d'ordine locale in due punti vicini (per K = O le correlazioni sono nulle, mentre per K = 1 le correlazioni sono massime: tutti gli spins devono avere lo stesso segno); il parametro K1 è connesso alla temperatura dalla relazione K1 = th(β).
In questo caso le equazioni (19) diventano
Formula (20)
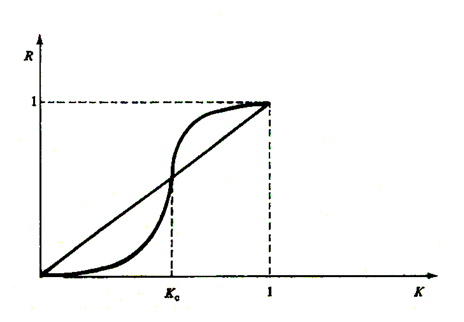
dove adesso R è una normale funzione. Se la forma di R è quella mostrata nella fig. 13, l'equazione per K∞ ha solamente 3 soluzioni:
0. KC, 1. (21)
La prima e l'ultima corrispondono al punto fisso ad alta e bassa temperatura, mentre la soluzione di mezzo corrisponde al comportamento alla temperatura critica:
th(J/kTC) = KC. (22)
La trasformazione può essere studiata graficamente: non appena K1 è più grande (più piccolo) di KC, K∞, è uguale a 0 o a 1.
La temperatura critica è fissata dall'equazione (22); un calcolo più dettagliato mostra che
ν = l/[log2(dR/dK)], K = KC. (23)
L'esponente critico η, definito dall'equazione (15), si ottiene studiando l'effetto di un campo magnetico; tutti gli altri esponenti critici si ottengono a partire da η e ν. Infatti si può dimostrare che le seguenti relazioni fra esponenti critici sono vere indipendentemente dal modello:
Formula. (24)
Queste relazioni sono ben soddisfatte sperimentalmente.
Usando approssimazioni più elaborate, in cui la distribuzione di probabilità dipende da molti parametri, si possono ottenere stime molto accurate degli esponenti critici (l'errore è dell'ordine di 10-3); per esempio, utilizzando una distribuzione di probabilità che dipende da 7 parametri, si trova ν = 0,631 ± 0,002, η = 0,031 ± 0,004; questi risultati devono essere confrontati con i valori ottenuti mediante un calcolo diretto: ν = 0,629 ± 0,003, η = 0,031 ± 0,005 (v. Zinn Justin, 1981). Un ulteriore calcolo, basato su una formulazione leggermente differente del gruppo di rinormalizzazione, porta ai seguenti valori: ν = 0,630 ± 10,0015, η = 0,031 ± 0,004 (v. Parisi, 1980). L'accordo fra i vari risultati è estremamente buono.
Riassumendo, supponiamo di avere un sistema fisico nel quale accadano fenomeni interessanti su scale diverse. Ci saranno delle variabili che descrivono accuratamente quello che succede su una scala data (e quindi su ogni scala più grande) e delle equazioni che permettono di calcolare che valori assumono queste variabili (le ‛leggi del moto', in breve). Nel caso che abbiamo visto le variabili sono le pL mentre le ‛leggi del moto' sono le distribuzioni di probabilità PL.
L'idea di base del gruppo di rinormalizzazione consiste nel concentrare l'attenzione su come le ‛leggi del moto' cambino quando si passa dalla descrizione su una scala a quella su un'altra scala. Da questo punto di vista il gruppo di rinormalizzazione ha una portata estremamente più vasta delle transizioni di fase del second'ordine. Per esempio, risultati spettacolari sono stati recentemente ottenuti (v. Collet ed Eckmann, 1980) per la transizione al caos nei sistemi dinamici (v. termodinamica irreversibile e sinergica, cap. 4, § e) ed esiste una speranza diffusa che il gruppo di rinormalizzazione possa essere uno strumento valido per lo studio della turbolenza per alti valori del numero di Reynolds (v. Frisch e altri, 1978).
BIBLIOGRAFIA
Ahlers, G., Thermodynamics and experimental tests of static scaling and universality near the superfluid transition on He4 under pressure, in ‟Physical review A", 1973, VIII, pp. 530-568.
Amit, D., Field theory, the renormalization group and critical phenomena, New York 1978.
Baracca, A., Manuale critico di meccanica statistica, Catania 1980.
Collet, P., Eckmann, J.P., Iterated maps on the interval as dynamical systems, Boston 1980.
Domb, C., Green, M.S. (a cura di), Phase transitions and critical phenomena, 4 voll., New York 1972-1980.
Frisch, U., Sulem, P.L., Nelkin, M., A simple dynamical model of intermittent fully developed turbulence, in ‟Journal of fluid mechanics", 1978, LXXXVII, pp. 719-736.
Gell-Mann, M., Low, F., Quantum electrodynamics at small distances, in "Physical review", 1954, XCV, pp. 1300-1312.
Gennes, P.-G., de, Superconductivity of metals and alloys, New York 1966.
Griffith, R.B., Non analytic behavior above the critical point in a random Ising ferromagnet, in "Physical review letters", 1969, XXIII, pp. 17-19.
Guggenheim, E.A., The principle of corresponding states, in "Journal of chemical physics", 1945, XIII, pp. 253-261.
Huang, K., Statistical mechanics, New York 1967.
Ising, E., Beitrag zur Theorie des Ferromagnetismus, in "Zeitschrift für Physik"", 1925, XXXI, pp. 253-258.
Kadanoff, L.P. e altri, Static phenomena near critical points: theory and experiments, in ‟Review of modern physics", 1967, XXXIX, pp. 395-431.
Kirkpatrick, S., Swenson, R.H., Statistical mechanics and disordered systems, in "Communciations of the ACM", 1985, XXVIII, pp. 363-371.
Kittel, C., Introduction to solid state physics, New York 1966.
Landau, L.D., Lifschitz, E.M., Staticeskaja fizika, Moskva 1971 (tr. it.: Fisica statistica, Roma 1978).
Langer, J., Theory of the condensation point, in ‟Annals of physics", 1967, XLI, pp. 108-157.
Lynton, E.A., Superconductivity, New York 1962.
Ma, S.K., Statistical mechanics, Singapore 1985.
Mc Coy, B.M., Wu, T.T., The two-dimensional Ising model, Cambridge, Mass., 1978.
Mezard, M., Parisi, G., Virasoro, M., Spin glass theory and beyond, Singapore 1986.
Parisi, G., Field-theoretic approach to second-order phase transitions in two- and three-dimensional systems, in "Journal of statistical physics", 1980, XXIII, pp. 49-82.
Parisi, G., Statistical field theory, New York 1986.
Stueckelberg, E.C.G., Peterson, A., La normalisation des constantes dans la théorie des quanta, in "Helvetica physica acta", 1953, XXVI, pp. 499-520.
Wilson, K.G., Renormalization group and critical phenomena. I. Renormalization group and the Kadanoff scalnig picture, in "Physical review B", 1971, IV, pp. 3174-3183.
Wilson, K.G., Problemi fisici con più scale di grandezza, in "Le scienze", 1979, CXXXIV, pp. 41-49.
Wilson, K.G., Kogut, J., The renormalization group and the expansion, in "Physics letters, section C: physics reports", 1974, XII, pp. 175-199.
Zinn Justin, J., Accurate values for the critical exponents, in Phase transitions (a cura di M. Levy, J.C. Le Guillou, J. Zinn Justin), New York 1981.