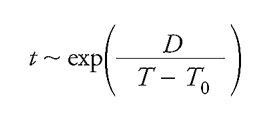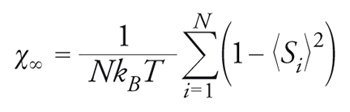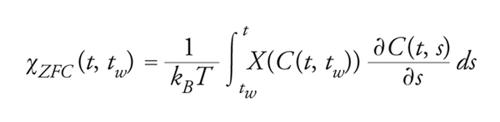Vetri: fenomeni di non equilibrio
Vetri: fenomeni di non equilibrio
È noto e ben compreso dal punto di vista teorico che la materia in equilibrio si può presentare sotto forma solida, liquida o gassosa. I liquidi e i gas di cui abbiamo esperienza quotidiana, preparati in stati arbitrari e successivamente isolati, tendono più o meno rapidamente a manifestare rilassamento verso stati finali stazionari (ossia stati di equilibrio termodinamico), dipendenti dalle condizioni esterne di temperatura e di pressione. Anche i solidi cristallini si trovano in stati di equilibrio; tuttavia, in molti sistemi il raggiungimento dello stato di equilibrio cristallino è assai difficile ed estremamente lento. Molti dei corpi solidi che ci circondano non sono cristalli, ma vetri (più precisamente vetri strutturali) che possono rimanere lontani dall'equilibrio termodinamico per tempi lunghissimi (infiniti a tutti gli effetti pratici).
La vetrificazione è una proprietà osservata in molti sistemi, alcuni monoatomici (vetri di fosforo, zolfo e selenio), altri, più numerosi, molecolari: ossidi (per es., gli ossidi di silicio che formano i vetri dell'esperienza quotidiana), miscele binarie, nitrati, leghe organiche, sistemi polimerici, metalli e così via. Nelle condizioni di temperatura e pressione in cui si osservano i vetri, lo stato di equilibrio termodinamico è in genere cristallino. Nei cristalli, gli atomi oscillano intorno ai nodi di reticoli spaziali ideali.
I vetri, pur essendo incapaci di fluire e dunque essendo meccanicamente solidi, si presentano, dal punto di vista strutturale, come materiali amorfi. Le posizioni spaziali degli atomi appaiono ‒ a parte piccole fluttuazioni locali ‒ come congelate nello spazio, in conformazioni simili (e altrettanto disordinate) a quelle del liquido ad alta densità da cui possono derivare per raffreddamento.
Non bisogna pensare che i fenomeni vetrosi si limitino al congelamento delle posizioni degli atomi in liquidi ad alta densità. Esistono materiali in cui le variabili che subiscono congelamento hanno natura molto diversa. I vetri di spin, per esempio, sono magneti amorfi in cui i fenomeni vetrosi riguardano il congelamento dei momenti magnetici, o spin, del sistema. Essi sono diventati esempi paradigmatici di sistemi a dinamica lenta e con dipendenza dalla storia termica delle grandezze termodinamiche osservate, e costituiscono forse i fenomeni di non equilibrio più caratteristici dello stato vetroso. Altri esempi comprendono vetri di vortici nelle fasi disordinate nei superconduttori di tipo II, vetri dipolari nei sistemi di momenti elettrici e così via.
La natura di non equilibrio dello stato vetroso non permette di studiarne il comportamento nell'ambito della termodinamica classica e ciò ha per lungo tempo rappresentato, e in parte rappresenta ancora, una difficoltà per la comprensione teorica fondamentale della natura dello stato vetroso. Negli ultimi decenni, lo studio sperimentale e teorico dei fenomeni di rilassamento lenti ha messo in evidenza leggi di scala dinamiche e comportamenti universali che fanno intravedere la possibilità di descrivere gli stati vetrosi in termini fisico-statistici, così come accade per gli stati di equilibrio.
Ci concentreremo qui su vetri stutturali e vetri di spin, che presentano fenomenologie a cui molti altri tipi di vetri sembrano ricondursi. Gran parte della fenomenologia di non equilibrio dei sistemi vetrosi può essere descritta nell'ambito della fisica classica.
La formazione dei vetri strutturali
Alcune proprietà dei vetri strutturali possono essere comprese sulla base della loro formazione a partire dalla fase liquida. In natura esistono sia liquidi che cristallizzano, sia liquidi che, più o meno facilmente, formano vetri. Questa proprietà è in genere associata alla natura dei costituenti elementari del sistema: più le unità sono semplici ‒ per esempio i sistemi monoatomici ‒ più il sistema sarà facilitato a formare uno stato cristallino; più le unità sono complesse ‒ per esempio i sistemi polimerici ‒ più la cristallizzazione sarà difficile e il sistema tenderà a formare stati vetrosi. Se, raffreddando un liquido, il punto di transizione allo stato cristallino è attraversato abbastanza rapidamente, la cristallizzazione può essere evitata e il sistema rimane in uno stato di equilibrio metastabile di liquido sottoraffreddato che, a parte differenze quantitative di densità, viscosità, energia interna, ecc., mantiene proprietà qualitative della fase liquida. Con l'abbassamento della temperatura, lo stato di liquido sottoraffreddato diventa più denso e viscoso. Sia la viscosità, η, sia il tempo di rilassamento strutturale, τ, ossia il tempo necessario affinché la forma del sistema si adatti alle sollecitazioni esterne, crescono molto rapidamente al diminuire della temperatura. La loro dipendenza dalla temperatura è ben descritta da un andamento di tipo Vogel-Fulcher:
[1] formula.
dove T è la temperatura, mentre D e T0 sono parametri fenomenologici che variano da materiale a materiale.
Nella vicinanza di una temperatura caratteristica Tg (detta temperatura di transizione vetrosa, maggiore di T0 di ca. il 10÷15%), il tempo di rilassamento è maggiore del tempo di osservazione, che può variare, a seconda degli esperimenti, da poche ore a molti anni. In tali condizioni il sistema non riesce ad adeguare il proprio stato alle sollecitazioni esterne e si comporta, dal punto di vista meccanico, come un solido; il sistema esce quindi dallo stato di liquido metastabile ed entra in uno stato congelato, che per alcuni materiali può durare anche tempi geologici. Esiste un valore convenzionale della viscosità per stabilire la separazione dello stato liquido da quello vetroso, pari a 1013 Poise e corrispondente a un tempo di rilassamento di alcune ore. La legge di Vogel-Fulcher descrive bene i dati sperimentali fino alla temperatura Tg, punto al di sotto del quale il tempo di rilassamento all'equilibrio diventa troppo grande per poter essere misurato. Rimane aperta la questione se questa legge sia valida anche a temperature più basse di Tg, per le quali predice un tempo di rilassamento divergente alla temperatura finita T0.
Il valore della temperatura di congelamento Tg dipende debolmente, ma percettibilmente, dalla velocità di raffreddamento e risulta tanto più basso quanto più il raffreddamento è lento. Tale dipendenza dimostra come la transizione vetrosa sia un fenomeno di non equilibrio. Nella fase vetrosa, il sistema si trova in stati metastabili con una vita propria lunga: grandezze fisiche, come per esempio l'energia interna e la densità, cessano di essere funzioni di stato (dipendenti, cioè, soltanto da parametri come temperatura e pressione esterne), ma sono determinate anche dalla storia termica, cioè dal percorso che ha portato ai valori dei parametri di stato assunti dal sistema. Il passaggio dalla fase liquida al vetro, sebbene non comporti cambiamenti qualitativi nella disposizione microscopica degli atomi nello spazio, implica cambiamenti nelle proprietà fisiche macroscopiche come energia, calore specifico, compressibilità, ecc., simili a quelli osservati nelle transizioni di fase di equilibrio. Per temperature comprese entro uno stretto intervallo intorno a Tg, il calore specifico e la compressibilità subiscono bruschi salti, da valori caratteristici delle fasi liquide a valori più bassi, caratteristici delle fasi solide. Questo fenomeno trae origine dal congelamento strutturale, che avviene intorno alla transizione vetrosa.
Nella fase liquida ad alta densità, al di sopra di Tg si formano strette gabbie, in cui gli atomi sono imprigionati dai propri vicini. Si può ipotizzare che per T>Tg il rilassamento sia conseguenza di due processi, attivi su scale di tempo molto diverse: moti veloci di agitazione termica all'interno delle gabbie e moti lenti di diffusione che coinvolgono in movimenti collettivi numerosi atomi e portano all'apertura delle gabbie. Mentre i moti veloci riescono ad adattarsi rapidamente ai cambiamenti della temperatura esterna, i moti diffusivi diventano via via più lenti, fino a che, al di sotto della temperatura di transizione vetrosa, risultano a tutti gli effetti congelati. È possibile, pertanto, interpretare il salto del calore specifico nell'ambito della termodinamica. Grazie alla separazione tra le scale di tempo dell'agitazione termica locale e la diffusione, è possibile separare i due corrispondenti contributi nell'entropia: l'entropia vibrazionale e l'entropia configurazionale. L'una, seguendo la prima legge della termodinamica, è disponibile per scambi di calore per temperature sia superiori sia inferiori a quella di transizione; l'altra, al di sotto della temperatura di transizione, cessa di essere disponibile a causa del congelamento dei corrispondenti gradi di libertà.
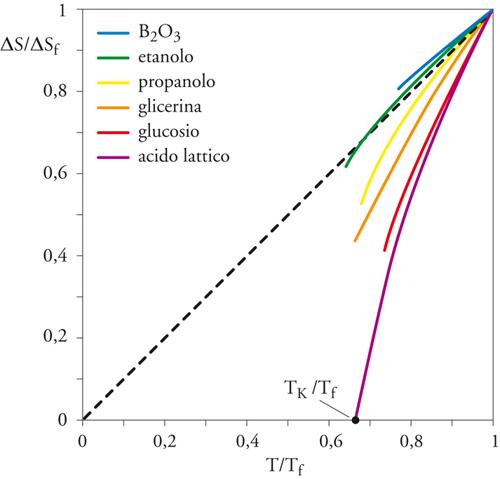
La parte configurazionale corrisponde, secondo l'interpretazione statistica dell'entropia, a una molteplicità esponenziale di possibili stati vetrosi, microscopicamente differenti ma con analoghe proprietà macroscopiche. È una funzione crescente della temperatura (fig. 2) ed estrapolazioni al di sotto di Tg suggeriscono che possa annullarsi a una temperatura finita TK, detta temperatura di Kauzmann. Secondo alcuni modelli teorici, tale temperatura corrisponderebbe a un punto di transizione vetrosa termodinamica ideale e coinciderebbe con la temperatura T0 dell'equazione [1]. La transizione vetrosa, osservata in laboratorio per velocità di raffreddamento finite, sarebbe allora un riflesso di questa transizione ideale. Purtroppo, malgrado tale scenario sia di notevole interesse, è difficile verificarne l'attendibilità, perché, a causa del forte aumento del tempo di rilassamento, risulta impossibile misurare l'entropia del liquido per temperature vicine alla temperatura TK stimata. È degno di nota che, nei modelli disordinati con interazioni a lungo raggio, la transizione vetrosa avvenga con un meccanismo di crisi entropica analogo a quello sopra menzionato. Rimane aperta per la ricerca futura la questione se la transizione ideale possa esistere nei vetri reali.
Non bisogna credere che lo stato di non equilibrio raggiunto alla transizione vetrosa persista perfettamente immutato nel corso del tempo. Processi di rilassamento strutturale, impercettibili su scale di tempo brevi, ma misurabili su scale di tempo opportunamente lunghe, tendono ad avvicinare il sistema a stati di minore energia. Così, quantità 'a un tempo', come l'energia interna, la densità, ecc., evolvono lentamente, mentre quantità 'a due tempi', come le funzioni di correlazione tra quantità fisiche a tempi successivi e le funzioni di risposta ritardata a perturbazioni esterne, mostrano comportamenti di rilassamento di non equilibrio. Si tratta di processi che rivestono notevole importanza pratica, nella scelta di materiali vetrosi in base alle loro caratteristiche fisiche, e di fondamentale interesse teorico, per il ruolo centrale che hanno assunto in tempi recenti nella comprensione fisica dello stato vetroso.
Il congelamento nei vetri di spin
La vetrificazione dei liquidi ha un analogo magnetico nei vetri di spin. I sistemi magnetici sono materiali solidi in cui i gradi di libertà fondamentali sono le orientazioni spaziali dei momenti magnetici degli atomi, o spin. Essi interagiscono a coppie mediante le cosiddette interazioni di scambio. I vetri di spin sono sistemi magnetici amorfi, in cui i momenti magnetici occupano posizioni aleatorie all'interno di materiali non magnetici. Questi materiali sono in un certo senso intermedi tra i ferromagneti, per i quali le interazioni di scambio sono positive e tendono a orientare gli spin nella medesima direzione, e gli antiferromagneti, in cui le interazioni sono negative e tendono a orientarli in direzioni opposte. Nei vetri di spin le interazioni oscillano e assumono valori sia positivi sia negativi in funzione della distanza tra gli spin. La presenza di interazioni di segno opposto può portare a frustrazione, cioè all'impossibilità di trovare configurazioni degli spin tali che tutte le interazioni risultino soddisfatte. In presenza di disordine e frustrazione, il raggiungimento di stati di bassa energia è un problema di ottimizzazione complicato: il sistema fisico deve risolverlo secondo una ricerca di tipo locale, esplorando configurazioni vicine per tempi vicini, e ostacoli provengono da vari tipi di barriere o di 'strettoie' energetiche.
I vetri di spin, che hanno proprietà paramagnetiche ad alte temperature, mostrano comportamento vetroso a temperature basse, per le quali si ha il congelamento degli spin in orientazioni aleatorie. La transizione vetrosa assume, in maniera diversa rispetto ai vetri strutturali, i caratteri di una transizione termodinamica. In confronto alle corrispondenti quantità dei vetri strutturali, le quantità a un tempo dei vetri di spin mostrano effetti di dipendenza dalla storia termica molto meno pronunciati: fissata la temperatura al valore finale, esse sembrano rilassare, seppure lentamente, verso valori indipendenti dalla storia termica, identificabili con i valori di equilibrio. Il processo di congelamento è abitualmente rilevato mediante lo studio della risposta a un piccolo campo magnetico, che induce una magnetizzazione M, ossia un'orientazione media degli spin, in direzione del campo, secondo la seguente relazione:
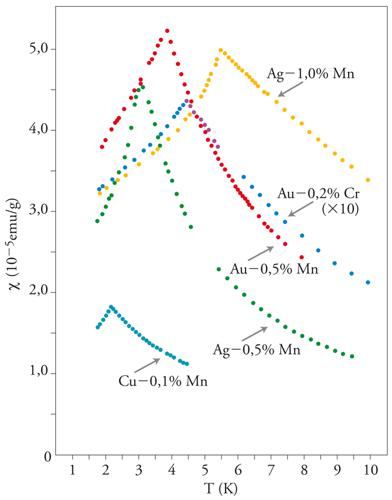
[2] M = χ∞h
valida per campi sufficientemente piccoli, dove la costante χ∞, detta suscettività lineare statica, è una funzione della temperatura. Questa mostra un comportamento singolare con una cuspide (fig. 3) a una temperatura caratteristica Tg. Tale temperatura è riproducibile in esperimenti corrispondenti a differenti storie termiche e a diversi campioni della stessa sostanza. Alla stessa temperatura la suscettività non lineare, che descrive il termine successivo nello sviluppo della magnetizzazione come funzione del campo, mostra una divergenza con legge di potenza, nella maniera caratteristica delle transizioni di fase del secondo ordine.
Nell'ipotesi che esista un equilibrio termico sia al di sopra sia al di sotto della temperatura di transizione Tg, la teoria della risposta lineare permette di interpretare la cuspide nella suscettività come un congelamento dei momenti magnetici locali. Se, infatti, si denota con le parentesi angolari 〈 〉 la media termica e si considera per semplicità il caso di spin con due possibili orientazioni Si=±1 (variabili di Ising), nei vetri di spin la suscettività magnetica χ∞ verifica la relazione:
[3] formula,
dove N è il numero di spin del sistema, T la temperatu-ra, kB la costante di Boltzmann; abbiamo inoltre posto, per semplicità, uguale a 1 il fattore di proporzionalità tra spin e momenti magnetici. Ad alta temperatura, i valori medi locali degli spin sono nulli 〈Si〉=0 e la suscettività segue la legge di Curie χ∞=1/kBT. Deviazioni da tale andamento sono conseguenza di valori medi non nulli. Il punto di cuspide nella fig. 3 corrisponde alla temperatura al di sotto della quale i valori medi 〈Si〉 sono diversi da zero. Le direzioni intorno alle quali gli spin si congelano non corrispondono ad alcun tipo di ordine a lungo raggio, in particolare la magnetizzazione globale M=(∑Ni=1〈Si〉)/N è nulla in tutta la regione di bassa temperatura. La fluttuazione media della magnetizzazione (parametro di Edwards-Anderson) qEA=(∑i〈Si〉2)/N può essere considerata il parametro d'ordine che caratterizza la transizione, nullo nella fase di alta temperatura e non nullo nella fase vetrosa.
Fenomeni d'invecchiamento e dinamica lenta
Sia nei vetri strutturali, per i quali la transizione vetrosa è un fenomeno di non equilibrio, sia nei vetri di spin, per i quali la transizione ha carattere termodinamico, lo studio di quantità dinamiche rivela il perdurare di processi di rilassamento di non equilibrio nella fase congelata. Descriveremo ora i protocolli sperimentali classici usati per rilevare tali processi nel caso dei vetri di spin. Gli stessi protocolli sono usati, mutatis mutandis, per altri tipi di vetro. Le procedure prevedono un raffreddamento rapido, idealmente istantaneo, da una temperatura iniziale maggiore di Tg a una temperatura finale minore di Tg. Il sistema è in seguito lasciato rilassare liberamente per un tempo di attesa, o età, tw; a tempi t>tw sono effettuate misurazioni di risposta lineare rispetto a variazioni di un campo magnetico esterno. Due versioni complementari sono prese comunemente in considerazione: negli esperimenti ZFC (Zero field cooled), il campione è raffreddato e lasciato rilassare liberamente in assenza di campo; dopo un tempo di attesa tw, è introdotto istantaneamente un piccolo campo h e, per tempi t successivi, è osservato il rilassamento della magnetizzazione MZFC(t,tw)=hχZFC(t,tw) verso il valore asintotico, diverso da zero. Negli esperimenti TRM (Thermo-remanent magnetization), il campione è raffreddato e lasciato rilassare in presenza di un debole campo magnetico h, che induce una magnetizzazione non nulla; al tempo tw, il campo è rimosso ed è quindi studiato il rilassamento temporale della magnetizzazione MTRM(t,tw)=hχTRM(t,tw) verso il valore nullo. Il tempo tw è normalmente scelto abbastanza lungo, perché nell'esperimento ZFC la magnetizzazione M sia ben stabilizzata vicino al valore asintotico M(h)=χ∞h. La complementarità degli esperimenti è espressa dalla relazione tra le suscettività dinamiche χZFC(t,tw)+χTRM(t,tw)=χ∞, valida in regime di risposta lineare.
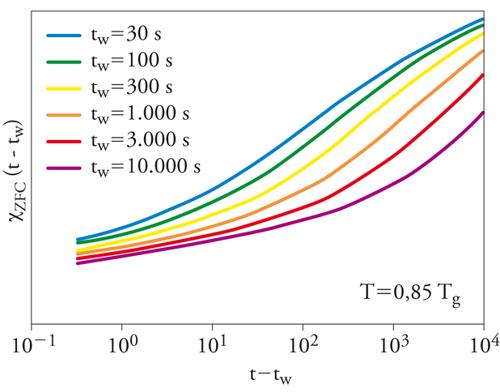
Se il sistema fosse capace di raggiungere l'equilibrio, o se restasse rigorosamente bloccato in uno stato metastabile, in condizioni di equilibrio per tw sufficientemente grande ci si attenderebbe un comportamento stazionario invariante per traslazioni temporali: i valori misurati della magnetizzazione dovrebbero dipendere esclusivamente dal tempo intercorso, t−tw, dalla rimozione (esperimenti TRM) o dall'introduzione (esperimenti ZFC) del campo magnetico. Questo è quello che accade al di sopra della temperatura Tg; per temperature inferiori a Tg si riscontra il fenomeno dell'invecchiamento, lo stato del sistema è cioè in lenta evoluzione e dipende dall'età tw. Nella magnetizzazione si osserva dipendenza sia da t−tw sia da tw. Nella fig. 4 è mostrato il comportamento della suscettività χZFC(t,tw) in un tipico esperimento d'invecchiamento a bassa temperatura in funzione di t−tw.
L'analisi dei dati sperimentali mostra che, per tempi t−tw dello stesso ordine di grandezza di tw, si ha invarianza di scala: le curve di rilassamento corrispondenti a tempi di attesa diversi possono essere messe in relazione le une con le altre riscalando le differenze t−tw secondo un opportuno tempo di rilassamento efficace τ(tw), crescente con il tempo di attesa tw e apparentemente divergente con esso. Per intervalli temporali entro i quali è stato possibile effettuare esperimenti, il tempo di rilassamento efficace segue una legge di potenza τ(tw)∼twα, con valori tipici di α=0,8÷0,9. In questi sistemi, le leggi di scala suggeriscono che i fenomeni di invecchiamento possano persistere indefinitamente, rallentando continuamente senza mai fermarsi. La violazione dell'invarianza per traslazioni temporali ha condotto alla ricerca di altre indicazioni capaci di chiarire la natura della dinamica di non equilibrio. In condizioni di equilibrio, la suscettività χTRM(t,tw) è legata alla funzione di correlazione temporale tra le fluttuazioni spontanee della magnetizzazione in assenza di campo C(t−tw)=N〈M(t)M(tw)〉 dal teorema fluttuazione-dissipazione: χTRM(t,tw)=C(t−tw)/kBT. Violazioni di tale relazione, originariamente messe in evidenza mediante simulazioni di modelli tridimensionali, sono state di recente osservate sperimentalmente e hanno assunto una grande importanza nella teoria dello stato vetroso.
Modelli disordinati
Per descrivere la difficoltà dei sistemi vetrosi a raggiungere l'equilibrio, si ricorre spesso alla metafora del cosiddetto paesaggio di energia potenziale. Si possono pensare le configurazioni di un sistema fisico, sia esso composto da particelle, da spin o da gradi di libertà di altra natura, come punti in uno spazio, chiamato spazio delle configurazioni, in cui a ogni grado di libertà corrisponde una diversa coordinata e in cui il valore dell'energia potenziale è raffigurato come un'elevazione da una quota arbitraria. Un paesaggio energetico liscio o levigato, formato per esempio da una regione concava con un unico minimo, non presenta impedimenti alla termalizzazione. Sistemi di questo tipo sono ergodici, cioè capaci di esplorare liberamente tutto il paesaggio nel corso dell'evoluzione temporale. Al contrario, un paesaggio complesso, con molte valli, barriere, strettoie, presenta ostacoli all'esplorazione dello spazio e può dare luogo a fenomeni vetrosi. Tali asperità possono impedire o fortemente rallentare il rilassamento, fino a indurre fenomeni di violazioni dell'ergodicità, per cui porzioni di paesaggio sono dinamicamente inaccessibili.
L'analisi teorica dei paesaggi di sistemi realistici, sia nel caso di vetri strutturali, sia in quello di vetri di spin, risulta tecnicamente proibitiva con i metodi attualmente disponibili. I modelli di campo medio per i vetri di spin utilizzano strutture semplificate del paesaggio complesso, accessibili a uno studio analitico sia per le proprietà di equilibrio, sia per la dinamica di non equilibrio. La semplificazione maggiore dei modelli di campo medio, peraltro correntemente usati in molti campi della fisica, consiste nel trascurare l'organizzazione geometrica degli spin nello spazio tridimensionale. Fondamento dell'applicabilità di tali modelli è l'idea che la similarità dei fenomeni vetrosi in vari materiali rifletta proprietà universali comuni a un gran numero di sistemi differenti. La validità di tale ipotesi è correntemente dibattuta all'interno della comunità scientifica e le indicazioni in suo favore sono principalmente di carattere fenomenologico.
Dalla teoria di campo medio emerge un quadro coerente dei fenomeni vetrosi e della dinamica di invecchiamento. Le simulazioni su sistemi più realistici, che permettono lo studio di quantità di interesse teorico e di non facile accesso sperimentale, rappresentano una guida importante per ottenere conferme riguardo gli scenari proposti. Schemi teorici approssimati per sistemi realistici, come per esempio la teoria dei modi accoppiati (mode coupling theory) o la cosiddetta approssimazione HNC (Hyper-netted chain), forniscono, in ambito rispettivamente dinamico e di equilibrio, descrizioni teoriche analoghe a quelle dei vetri di spin di campo medio. Il modello di riferimento nella teoria di campo medio dei vetri di spin considera sistemi di N spin con interazioni aleatorie a p corpi descritte dalla seguente funzione energia (hamiltoniana):
[4] H(S) = 1, N∑i1〈...〈ipJi1,...,ipSi1... Sip .;
Le costanti di accoppiamento Ji1,…,ip, fissate durante il moto degli spin, sono variabili casuali indipendenti con media nulla. Gli spin Si sono comunemente considerati come variabili di Ising Si=±1 o come variabili reali soggette al vincolo sferico ∑iSi2=N. Si può mostrare che due tipi di fenomenologia sono possibili, a seconda che il valore di p sia maggiore di due o uguale a due. Denoteremo rispettivamente i due casi come di tipo I e di tipo II.
Sistemi vetrosi di tipo I
L'equilibrio di questi sistemi è caratterizzato da tre fasi: una paramagnetica (o liquida), di alta temperatura, e due congelate, a bassa temperatura. Partendo dalla regione ad alta temperatura, dove il sistema è ergodico ed esplora liberamente lo spazio delle configurazioni, si incontra una prima transizione a una temperatura Tc, in corrispondenza della quale le configurazioni di equilibrio possono essere raggruppate in un numero esponenzialmente grande, exp(NΣ), di stati metastabili mutualmente inaccessibili e con tempo di vita infinito. La quantità Σ è identificata con l'entropia configurazionale: essa decresce per temperature decrescenti e si annulla a una seconda temperatura di transizione Ts minore di Tc, secondo uno scenario simile a quello della transizione allo stato di vetro ideale. Coerentemente con tale scenario, alla temperatura Ts l'energia libera mostra una singolarità, con un salto nel calore specifico. La dinamica di non equilibrio è studiata simulando teoricamente un raffreddamento istantaneo partendo da alte temperature. Al di sopra di Tc il sistema raggiunge lo stato di equilibrio in un tempo finito, mentre al di sotto cade in uno stato di non equilibrio con dinamica lenta e con fenomeni di invecchiamento. Il carattere della dinamica può essere valutato, in prima approssimazione, dalle quantità a un tempo, che nel limite asintotico tendono a valori stazionari, corrispondenti a una famiglia di stati metastabili di soglia, con energia libera più elevata di quella degli stati di equilibrio. È notevole che, dinamicamente, il salto del calore specifico tipico della transizione vetrosa sia osservato alla temperatura Tc.
Più interessante è il comportamento delle quantità a due tempi, dal quale si deduce che, sebbene l'evoluzione rallenti costantemente, il sistema non si ferma in alcuno degli stati metastabili. Lo studio della funzione di correlazione a tempi diversi, C(t,tw)=∑i〈Si(t)Si(tw)〉/N e della funzione di risposta coniugata in esperimenti ZFC, χZFC(t,tw), ha messo in evidenza una dinamica di non equilibrio caratterizzata da due regimi distinti, validi per tempi di invecchiamento tw lunghi. Il primo è un regime di equilibrio locale, valido per t−tw≪t,tw, nel quale la dinamica appare stazionaria, C(t,tw)∼Cst(t−tw), e la suscettività soddisfa la relazione di equilibrio del teorema fluttuazione-dissipazione χst(t−s)=(C(0)−Cst(t−s))/kBT; lecorrelazioni decrescono da C(0)=1 a un valore qEA>0, mentre la suscettività ZFC cresce da zero al valore χEA=(1−qEA)/kBT. Il secondo è un regime di invecchiamento che presenta invarianza di scala temporale, nel quale C(t,tw)∼Cinv((t−tw)/τ(tw)) e le correlazioni decrescono a partire da qEA. Il tempo di rilassamento efficace τ(tw) è una funzione crescente di tw, diverge per grandi tempi di attesa, ma, allo stadio attuale della teoria, non è stato ancora determinato teoricamente. I comportamenti delle correlazioni sono stati osservati in molti studi numerici su sistemi realistici.
Una delle previsioni più notevoli della teoria riguarda le violazioni della relazione di fluttuazione-dissipazione, che in questo regime risulta modificata in: χinv(t,tw)=χEA+X[qEA−Cinv((t−tw)/τ(tw))]/kBT. La X dipende dalla temperatura, verifica 0≤X〈1 ed è indipendente dal tempo per tempi grandi. Il sistema risponde in maniera normale, vale a dire secondo la relazione di equilibrio, su scale di tempo brevi, ma in maniera anomala, ossia violando la relazione di equilibrio, nel regime di invecchiamento. Di notevole importanza teorica è il fatto che la stessa costante governi il rapporto tra correlazione e risposta corrispondenti a diverse quantità osservabili. Essa è infatti legata alla crescita dell'entropia in funzione dell'energia libera dalla relazione X/T=∂Σ/∂f, la quale generalizza la relazione termodinamica che lega temperatura, energia ed entropia ed è intimamente connessa alla possibilità di considerare il rapporto T/X una temperatura efficace, che governa gli scambi di calore su scale di tempo comparabili all'età del sistema. La validità di tale relazione è alla base di una dettagliata descrizione statistica della dinamica nello stato vetroso e suggerisce relazioni termodinamiche modificate, per le quali tutta la dipendenza delle quantità osservabili dalla storia termica è riassunta nel valore della temperatura efficace.
Sistemi vetrosi di tipo II
In questi sistemi si ha un'unica temperatura di transizione, Tc, a cui sia la dinamica di non equilibrio sia la statica subiscono una transizione del secondo ordine. La suscettività magnetica statica esibisce in questo punto una singolarità a cuspide, indice di congelamento, in analogia con quanto avviene nel caso dei vetri di spin reali. L'equilibrio prevede molteplici stati ergodici, ma l'entropia configurazionale è nulla in tutta la fase di bassa temperatura. L'organizzazione degli stati nello spazio delle configurazioni sembra obbedire a un ordine gerarchico (ultrametricità) in cui le componenti ergodiche possono essere messe in corrispondenza ai punti terminali di un diagramma ad albero. Nella dinamica di non equilibrio, diversamente da quanto accade nei sistemi di tipo I, le quantità a un tempo tendono, per intervalli temporali lunghi, ai valori di equilibrio. Ciò, tuttavia, non è indice sufficiente del raggiungimento dell'equilibrio, poiché anche in questo caso il rapporto tra correlazione e risposta mette in evidenza fenomeni di invecchiamento, i quali generalizzano i comportamenti descritti nel precedente paragrafo. A differenza dei sistemi di tipo I, tuttavia, l'invecchiamento non può essere parametrizzato in termini di un'unica scala di tempo efficace τ(tw); piuttosto, si trovano un'infinità di scale di tempo gerarchicamente organizzate.
Se denotiamo con τ(q,tw) il tempo t che la correlazione impiega per decrescere dal valore C(tw,tw)=1 a un valore C(t,tw)=q, si ha che, per valori della correlazione q′>q, τ(q,tw) è molto maggiore di τ(q′,tw); più precisamente, il rapporto τ(q′,tw)/τ(q,tw) tende a zero per grandi tw. Inoltre, non abbiamo in questo caso un'unica temperatura efficace, ma a ogni scala di tempo corrisponde asintoticamente una diversa temperatura T/X(q). La relazione tra risposta ZFC e correlazione può essere scritta come:
[5] formula,
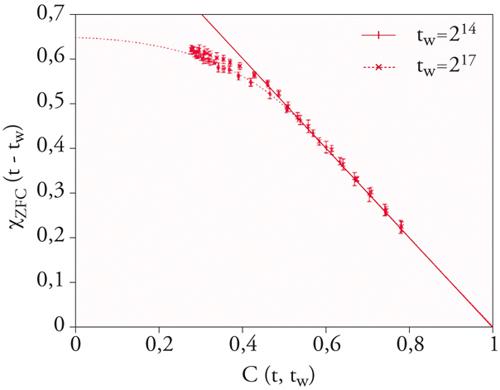
con la convenzione che, per q≥qEA, X(q)=1. È invalsa l'abitudine di descrivere le violazioni della relazione di fluttuazione-dissipazione rappresentando χZFC(t,tw) in funzione di C(t,tw) in grafici parametrici. La pendenza di tali curve fornisce, per tw grandi, il rapporto X(q)/T. La funzione X(q) è associata a un'analoga funzione che descrive le correlazioni tra le molteplici componenti ergodiche; la gerarchia tra scale di tempo trova così un corrispettivo nelle relazioni ultrametriche tra stati di equilibrio. Il rapporto (∂χZFC(t,tw)/∂tw)/(∂C(t,tw)/∂tw) può essere assunto, per tw fissati e tempi t tali che C(t,tw)=q, come definizione di una funzione X(q,tw)/T, da determinare sperimentalmente mediante misurazioni simultanee di correlazione e risposta. Si può ipotizzare che il suo valore sia equivalente, nel limite asintotico, a una misura delle correlazioni tra componenti ergodiche. Simulazioni numeriche nei modelli di vetro di spin in dimensione finita avvalorano l'ipotesi dell'esistenza di una funzione X(q) non banale (fig. 5). Recenti misure di X(q,tw) in materiali di vetro di spin reale mostrano un buon accordo qualitativo con la forma predetta dalla teoria.
Bibliografia
Angell 1995: Angell, C. Austen, Formation of glasses from liquids and biopolymers, "Science", 268, 1995, pp. 1924-1935.
Cugliandolo, Kurchan 1993: Cugliandolo, Leticia F. - Kurchan, Jorge, Analytical solution of the off-equilibrium dynamics of a long range spin-glass model, "Physical review letters", 71, 1993, pp. 173-176.
Cugliandolo 1997: Cugliandolo, Leticia F. - Kurchan, Jorge - Peliti, Luca, Energy flow, partial equilibration and effective temperatures in systems with slow dynamics, "Physical review E", 55, 1997, pp. 3898-3914.
Fischer, Hertz 1991: Fischer, Karl-Heinz - Hertz, John A., Spin glasses, Cambridge, Cambridge University Press, 1991.
Franz 1999: Franz, Silvio e altri, The response of glassy systems to random perturbations: a bridge between equilibrium and off-equilibrium, "Journal of statistical physics", 97, 1999, pp. 459-488.
Franz, Virasoro 2000: Franz, Silvio - Virasoro, Miguel Ángel, Quasi-equilibrium interpretation of aging dynamics, "Journal of physics A", 33, 2000, pp. 891-905.
Hérisson, Ocio 2002: Hérisson, Didier - Ocio, Miguel, Fluctuation-dissipation ratio of a spin glass in the aging regime, "Physical review letters", 88, 2002, pp. 257202-257205.
Marinari 1998: Marinari, Enzo e altri, Violation of the fluctuation dissipation theorem in finite dimensional spin glasses, "Journal of physics A", 31, 1998, pp. 2611-2620.
Mézard 1987: Mézard, Marc - Parisi, Giorgio - Virasoro, Miguel Ángel, Spin glass theory and beyond, Singapore, World Scientific, 1987.
Mézard, Parisi 2000: Mézard, Marc - Parisi, Giorgio, Statistical physics of structural glasses, "Journal of physics. Condensed matter", 12, 2000, pp. 6655-6673 (Proceedings of the ICTP-NIS conference on "Unifying concepts in glass physics", Trieste 1999, edited by Silvio Franz, Sharon C. Glotzer, Srikanth Sastry, Bristol, Institute of Physics, 2000).
Nieuwenhuizen 2000: Nieuwenhuizen, Theo M., Thermodynamic picture of the glassy state, "Journal of physics. Condensed matter", 12, 2000, pp. 6543-6552 (Proceedings of the ICTP-NIS conference on "Unifying concepts in glass physics", Trieste 1999, edited by Silvio Franz, Sharon C. Glotzer, Srikanth Sastry, Bristol, Institute of Physics, 2000).
Parisi 1979: Parisi, Giorgio, Toward a mean field theory for spin glasses, "Physics letters A", 73, 1979, pp. 203-205.
Sherrington, Kirkpatrick 1975: Sherrington, David - Kirkpatrick, Scott, Solvable model of a spin glass, "Physical review letters", 35, 1975, pp. 1792-1796.
Young 1998: Spin glasses and random fields, edited by A. Peter Young, Singapore-London, World Scientific, 1998.
Zarzycki 1982: Zarzycki, Jerzy, Les verres et l'état vitreux, Paris, Masson, 1982.