algebra

algebra

Quando le lettere funzionano meglio dei numeri

algebra

Si può dire che l'algebra inizia dove finisce l'aritmetica, perché introduce, attraverso il calcolo letterale, un modo nuovo, molto più generale, di rappresentare i numeri e le operazioni che si possono eseguire su di essi. Ma il vero obiettivo dell'algebra, o, meglio, di quella parte che viene chiamata algebra classica, è lo studio delle equazioni algebriche, un potente strumento matematico per risolvere vari problemi. Oltre all'algebra classica esiste però anche l'algebra moderna, che si occupa di strutture matematiche del tutto generali, come i gruppi

Calcolare usando lettere e non numeri

La storia dell'algebra ha inizio con gli Egiziani e i Babilonesi che già conoscevano le soluzioni per le equazioni di primo e secondo grado. Il termine algebra, però, deriva dalla parola araba al-giabr, usata per la prima volta dal matematico arabo Muhammad Ibn Musa al-Khuwarizmi (vissuto nel 9° secolo a Baghdad) per indicare l'operazione con cui si passa dall'eguaglianza A−B=C all'eguaglianza A=B+C. Nell'algebra le operazioni fondamentali dell'aritmetica sono trattate usando lettere al posto dei numeri e ciò permette di raggiungere soluzioni indipendenti dal caso considerato. Si possono così formulare in modo del tutto generale le leggi dell'aritmetica. Per esempio la proprietà commutativa dell'addizione, cioè il fatto che scambiando l'ordine degli addendi il risultato non cambia, si scrive come a+b=b+a. Questa identità vale in generale, indipendentemente dal valore assegnato ad a e b.

Attualmente l'algebra si divide in due parti: l'algebra classica e l'algebra moderna. L'algebra classica si occupa del calcolo letterale, delle espressioni miste numerico-letterali (monomi e polinomi) e, soprattutto, delle equazioni algebriche e dei relativi problemi e metodi per risolverle.

Un importante sviluppo della matematica si ebbe quando il filosofo e matematico francese René Descartes (Cartesio), nel Seicento, applicò l'algebra alla geometria, dando luogo a quella particolare disciplina che è la geometria analitica. L'algebra moderna si occupa, invece, di strutture matematiche molto generali, come i gruppi. Il francese Evariste Galois è stato il primo a studiare le equazioni servendosi dei gruppi a esse associati e per far questo ne ha approfondito la teoria generale.

Il calcolo letterale

Dalla geometria elementare sappiamo che per calcolare l'area di un quadrato dobbiamo moltiplicare la misura del lato per sé stessa. Se applichiamo questa regola generale al calcolo dell'area di un quadrato di lato 2 otteniamo 2×2=4. Nel linguaggio dell'algebra diventa possibile esprimere tale legge in tutta la sua generalità utilizzando il simbolo l per indicare la misura del lato. Da qui nasce la regola sempre valida l×l=l². Questa semplice espressione è un esempio di calcolo letterale, cioè di calcolo eseguito su numeri rappresentati da lettere dell'alfabeto. Lo studio dell'algebra inizia dal calcolo letterale, che serve, in primo luogo, per esprimere relazioni fra numeri in modo generale: la formula per calcolare l'area del quadrato vale, infatti, per tutti i quadrati, indipendentemente dalla misura del loro lato. Il calcolo letterale non si applica soltanto alla geometria, bensì a tutti quei casi in cui è necessario indicare una relazione, un'operazione, una legge in cui siano coinvolte grandezze rappresentabili mediante numeri. Per esempio, sappiamo che in fisica vale la legge scoperta da Newton, secondo cui, applicando una forza F a un corpo di massa m, si imprime al corpo stesso un'accelerazione a: F=ma.

Per rendersi conto dell'efficacia del calcolo letterale, si può ricorrere a un simpatico giochetto: pensate un numero, moltiplicatelo per 2, aggiungete 3 al risultato, aggiungete a questo il numero di partenza, dividete per 3 e poi togliete 1; il risultato è il numero che avete pensato. Non è necessario saper leggere nel pensiero per 'indovinare' il risultato: basta applicare il calcolo letterale. Chiamiamo a il numero pensato. Le operazioni indicate, scritte in simboli matematici, sono: (2a+3+a) : 3−1=(3a+3) : 3−1=a+1−1=a.

E questo risultato si ottiene indipendentemente dal numero a.

Operazioni algebriche

Il calcolo letterale permette di studiare le quattro operazioni elementari dell'aritmetica e le loro rispettive proprietà in modo del tutto generale. I simboli dell'algebra comprendono i numeri, le lettere e i segni delle operazioni. Tra le lettere, alcune rappresentano quantità costanti, altre quantità variabili. In genere per le costanti si usano le prime lettere dell'alfabeto (a, b, c, e così via), mentre per le variabili si adottano le ultime lettere dell'alfabeto, come x, y, w e z.

Dati due numeri, a e b, la loro somma si indicherà con a+b, la loro differenza con a−b, il loro prodotto, accostando le due lettere, con ab oppure, scrivendo un puntino (∙) fra loro, con a∙b, il loro quoziente con a/b. Per ciascuna operazione algebrica continuano a valere le proprietà della corrispondente operazione aritmetica. Per esempio, per la moltiplicazione le proprietà commutativa, associativa e distributiva si scrivono rispettivamente: ab=ba, abc=(ab)c=a(bc), a(b+c)=ab+ac. Per la moltiplicazione vale anche la legge di annullamento del prodotto. In base a questa legge, un prodotto, ab, si annulla se, e soltanto se, almeno uno dei due fattori a o b è zero.

I monomi

Si chiama monomio un'espressione algebrica (cioè contenente numeri e lettere) nella quale compaiono solamente operazioni di moltiplicazione e di divisione. Per esempio, la formula bh/2 che dà la misura dell'area di un triangolo di base b e altezza h è un monomio.

Si chiama coefficiente di un monomio la sua parte numerica. Si chiama grado di un monomio la somma degli esponenti delle potenze che formano la sua parte letterale. Due monomi che abbiano la stessa parte letterale si dicono simili. Monomi simili hanno, naturalmente, lo stesso grado. L'addizione fra due monomi, in generale, si indica scrivendoli uno dopo l'altro, ciascuno col proprio segno; la sottrazione, scrivendo il primo seguito dal secondo cambiato di segno. Nel caso particolare che i due monomi siano simili, la loro somma (oppure la loro differenza) si riduce a un monomio che ha come parte letterale la parte letterale comune ai due e come coefficiente la somma (differenza) dei coefficienti. Per esempio:

2ab²+5ab²=(2+5)ab²=7ab²

8abc−3abc=(8−3)abc=5abc

Il risultato della moltiplicazione (oppure delle divisione) fra due monomi è un monomio che ha come coefficiente il prodotto (oppure il quoziente) dei coefficienti dei due monomi. La sua parte letterale, invece, è formata, per la moltiplicazione, da tutte le lettere che compaiono nei monomi di partenza ciascuna col proprio esponente, mentre per la divisione è data dal rapporto fra le parti letterali dei monomi iniziali. La potenza di un monomio si ottiene elevando a quella potenza il coefficiente e moltiplicando gli esponenti delle varie lettere che formano la sua parte letterale per l'esponente della potenza, come in questo esempio: (3a2b)³=27a⁶b³.

I polinomi

Un polinomio è la somma algebrica di due o più monomi non simili e quindi contiene almeno un segno di addizione o di sottrazione. Alcuni esempi:

3a+b²; a+b+c; 7a²b³−12bc²+d⁴

Il primo polinomio riportato è un binomio perché è formato da due monomi, il secondo e il terzo, invece, sono trinomi perché formati da tre monomi.

Si chiama grado di un polinomio il grado del monomio di grado più alto fra quelli che lo formano; un polinomio si dice omogeneo se tutti i monomi che lo compongono hanno lo stesso grado.

Il polinomio 3a+b² è di secondo grado e non è omogeneo, perché il monomio 3a è di primo grado, mentre il monomio b² è di secondo grado. Il polinomio a+b+c è di primo grado e omogeneo. Il polinomio 7a²b³−12bc²+d⁴ è di quinto grado e non è omogeneo.

I polinomi si sommano, sottraggono, moltiplicano e dividono operando sui monomi che li compongono.

La moltiplicazione di un polinomio per un altro polinomio si esegue moltiplicando tutti i monomi del primo per tutti i monomi del secondo e sommando i vari prodotti:

(3a+5b)(2a−3c)=6a²−9ac+10ab−15bc

La divisione di un polinomio per un altro polinomio si esegue con un procedimento un po' laborioso, ma simile a quello che si usa per dividere due numeri. In questo caso, però, bisogna operare sia sui coefficienti numerici sia sulle parti letterali.

Spesso, se l'espressione algebrica assegnata è complicata, risulta utile fattorizzarla scomponendola nel prodotto di fattori più semplici. Per esempio, il polinomio 2x³+8x²y si può riscrivere come 2x² (x+4y) prendendo a fattore comune gli elementi comuni a entrambi i monomi.

Le equazioni di primo grado

Diciamo che due espressioni algebriche sono uguali se rappresentano lo stesso numero. Si può anche dire che fra le due espressioni sussiste una relazione di eguaglianza, indicata con il segno =. A sinistra del segno uguale c'è il primo membro dell'eguaglianza, mentre a destra abbiamo il secondo membro.

In algebra si considerano due tipi di eguaglianze, quelle che sono sempre vere e quelle che sono vere soltanto quando alle lettere che vi compaiono si sostituiscono determinati numeri. Per esempio, l'eguaglianza a (b+c)=ab+ac è sempre vera, quali che siano i numeri rappresentati dalle lettere a e b, mentre l'eguaglianza 3a−5=10 è vera soltanto se a rappresenta il numero 5, in tutti gli altri casi è falsa.

Un'eguaglianza che sia sempre vera si chiama identità, un'eguaglianza che sia vera soltanto quando alle lettere che vi compaiono si sostituiscono determinati numeri si chiama equazione. In un'equazione le incognite sono le lettere che vi compaiono. Le soluzioni o radici di un'equazione sono quei numeri che, sostituiti alle incognite, rendono l'equazione un'eguaglianza vera: in questo caso si dice che quei numeri soddisfano o verificano l'equazione.

Prendiamo ora in considerazione, in particolare, le equazioni più semplici: quelle a una sola incognita (che indicheremo con la lettera x) e di primo grado, cioè tali che l'incognita abbia come esponente 1. In generale, un'equazione di primo grado ha un'unica soluzione. Esistono due eccezioni: le equazioni impossibili, che non hanno nessuna soluzione, e le equazioni indeterminate, che hanno infinite soluzioni. Due equazioni con la stessa soluzione si dicono equivalenti. Date due equazioni equivalenti, per trovarne la radice si può risolvere l'una o l'altra. Ovviamente, conviene risolvere quella più semplice. Perciò, per risolvere una qualsiasi equazione bisogna trovare la più semplice equazione equivalente a quella data, trasformando l'equazione di partenza in un'altra che ammetta la stessa soluzione e sia molto più semplice da risolvere.

Per raggiungere l'obiettivo è utile una regola generale, nota come principio di equivalenza. Il principio afferma che applicando le stesse operazioni aritmetiche o algebriche a entrambi i membri di un'equazione l'eguaglianza rimane invariata. In particolare un'equazione si trasforma in un'altra a essa equivalente se si trasporta un qualsiasi suo termine da un membro all'altro cambiandolo di segno.

Equazioni di grado superiore al primo

Le equazioni hanno un'enorme importanza, non soltanto nella matematica, ma anche in altre discipline scientifiche, e persino nella vita di tutti i giorni, perché molti problemi si possono impostare in forma di equazione e, allora, la soluzione dell'equazione è anche la soluzione del problema.

Per esempio, la traiettoria seguita da un proiettile è parabolica e si può descrivere utilizzando una relazione del tipo ax²+bx+c=0. Abbiamo scritto un'equazione algebrica di secondo grado perché l'incognita compare elevata al quadrato. Per risolvere questa equazione esiste una formula di validità generale. All'inizio del 16° secolo i matematici italiani Scipione Dal Ferro, Niccolò Tartaglia e Gerolamo Cardano hanno trovato un metodo generale per risolvere in funzione dei coefficienti anche le equazioni di terzo grado. Un allievo di Cardano, Ludovico Ferrari, ha, poi, scoperto una soluzione esatta valida per le equazioni di quarto grado. Ma quando i matematici nei secoli successivi hanno cercato di trovare una formula analoga per le equazioni di quinto grado o per quelle di grado ancora superiore non hanno ottenuto alcun risultato: agli inizi dell'Ottocento, l'italiano Paolo Ruffini, il norvegese Niels Abel e il francese Evariste Galois hanno dimostrato in modo rigoroso che questa formula non esiste.

Nel 1799 il matematico tedesco Carl Friedrich Gauss ha dimostrato il teorema fondamentale dell'algebra in base al quale ogni equazione algebrica di grado n possiede esattamente n soluzioni nel campo dei numeri complessi.

Un concetto dell'algebra moderna: la struttura di gruppo

Nel passare dall'aritmetica all'algebra classica, cioè dal calcolo numerico al calcolo letterale, si è fatto un importante progresso nella generalizzazione dei risultati del pensiero matematico, cioè nel passaggio da casi particolari a casi generali. Riferendosi al teorema di Pitagora, per esempio, una cosa è scrivere 32+42=52 (dove 3 e 4 sono le misure dei cateti di un particolare triangolo rettangolo e 5 è la misura dell'ipotenusa dello stesso triangolo), tutt'altra cosa è scrivere a²+b²=c² (dove a e b rappresentano le misure dei cateti di un qualsiasi triangolo rettangolo e c rappresenta la misura della sua ipotenusa): l'espressione letterale è più generale di quella numerica, cioè vale per tutti i triangoli rettangoli e non soltanto per uno particolare.

Nel passare dall'algebra classica all'algebra moderna, si è compiuta un'ulteriore generalizzazione. Infatti se nell'algebra classica si definisce, per esempio, la somma e poi se ne studiano le proprietà (associativa, commutativa e via dicendo), nell'algebra moderna si stabiliscono prima le proprietà di cui un'operazione deve godere (associatività, commutatività, e così via) e si verifica poi che la somma è una delle tante operazioni che godono di tali proprietà.

strutture algebriche

L'algebra moderna, infatti, si occupa di insiemi di elementi non precisati (non si parla esplicitamente di numeri) e delle operazioni che si possono eseguire su di essi. Questi insiemi dotati di operazioni si chiamano strutture algebriche. La struttura algebrica più semplice è il gruppo, G, un insieme di elementi (a, b, c, ...) dotato di un'operazione (che indicheremo col simbolo '°') che a due elementi dell'insieme ne fa corrispondere un terzo. Questa operazione gode della proprietà associativa. Inoltre, dato un qualsiasi elemento a del gruppo, esiste (sempre nel gruppo) un unico elemento n, detto elemento neutro rispetto all'operazione °, tale che a°n=n°a=a. Infine, per ogni elemento a del gruppo, esiste un elemento ā tale che a° ā = ā °a=n.

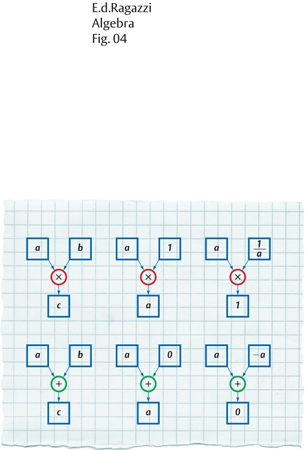
Si vede facilmente che l'operazione o può essere interpretata sia come addizione sia come moltiplicazione: nel primo caso, l'elemento neutro è 0 (infatti a+0=0+a=a) e ā è −a (infatti a+(−a)=(−a)+a=0); nel secondo caso, l'elemento neutro è 1 (infatti a×1=1×a=a) e ā è 1/a (infatti a×(1/a)=(1/a)×a=1).

Come risolvere un problema con le equazioni di primo grado

In un garage ci sono 36 veicoli, fra automobili e motociclette. Sapendo che la somma delle ruote dei veicoli (senza contare le ruote di scorta) è 132, trovare il numero delle automobili e quello delle motociclette.

Questo problema si può impostare in forma di equazione di primo grado. Infatti, chiamando x il numero delle automobili, il numero delle motociclette sarà 36−x. Siccome le automobili hanno 4 ruote e le motociclette 2, il numero totale delle ruote sarà dato dalla somma 4x+2(36−x). Allora, per trovare la risposta al nostro problema, basterà risolvere l'equazione

4x+2(36−x)=132

4x+72−2x=132

2x=132−72=60

x=60/2=30.

Siccome abbiamo chiamato x il numero delle automobili, le automobili sono 30 e le motociclette (36−30)=6.