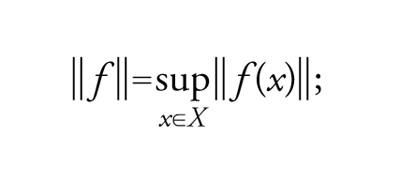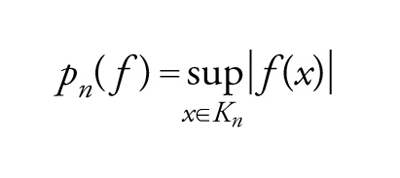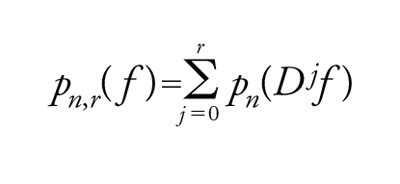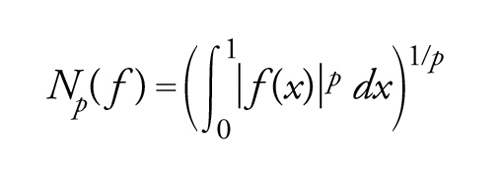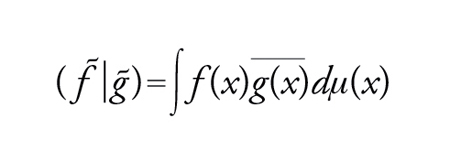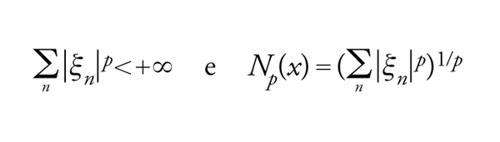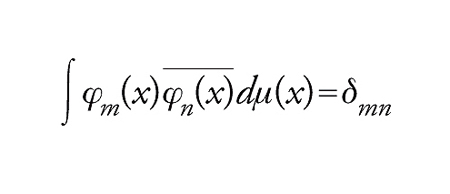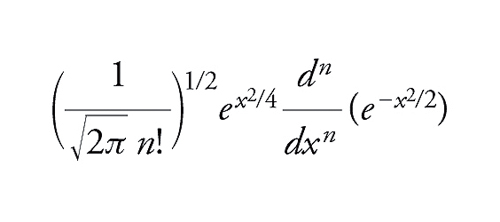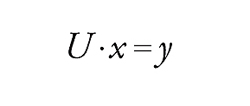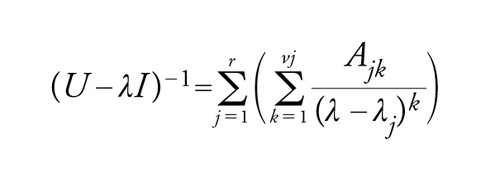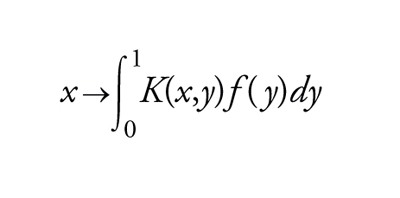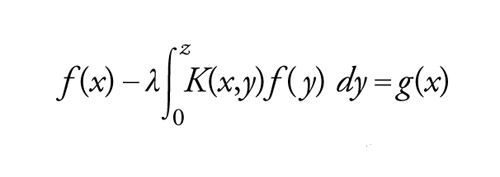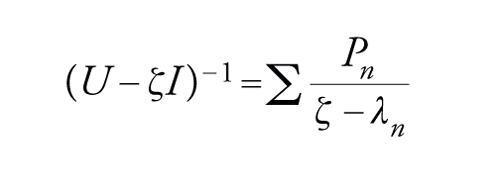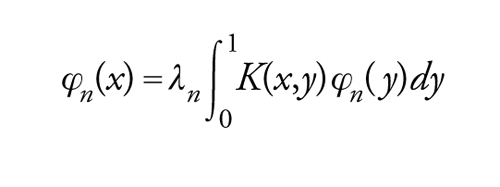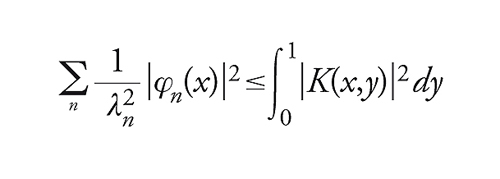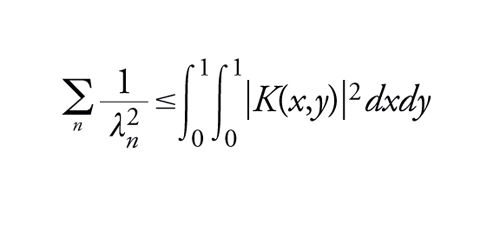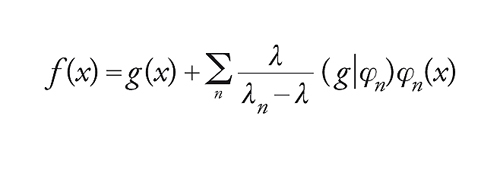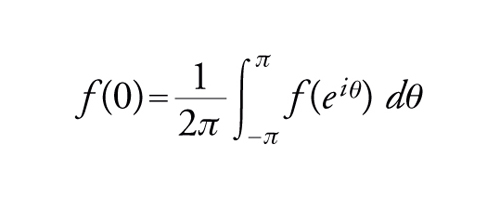Analisi matematica

Analisi matematica

Alcune delle idee fondamentali che sono alla base del calcolo risalgono ai Greci, ma il loro sviluppo sistematico iniziò soltanto nel XVII secolo. Alla fine di quel periodo, infatti, il concetto fondamentale di funzione reale di più variabili reali, la relativa interpretazione geometrica mediante un grafico e la natura delle due operazioni basilari del calcolo ‒ e cioè la differenziazione e l'integrazione ‒ erano sufficientemente chiariti. Ciò rese possibile ai matematici del XVIII sec. di imbarcarsi, con successo stupefacente, in un programma di applicazioni dei nuovi algoritmi ai più svariati problemi di matematica, meccanica, astronomia e fisica matematica: restando soltanto nel campo della matematica pura, la teoria delle equazioni differenziali, la teoria delle equazioni differenziali alle derivate parziali, il calcolo delle variazioni e la geometria differenziale sono tutti risultati conseguiti in quel periodo.

A ciò seguì, nel XIX sec., lo sviluppo della teoria delle funzioni analitiche di una variabile complessa e delle relative importanti applicazioni in tutti i rami della matematica, dalla teoria dei numeri alle rappresentazioni conformi e alla teoria del potenziale; il XIX sec. segnò pure la nascita della teoria dei gruppi di Lie, destinata a divenire uno dei filoni centrali della matematica contemporanea.

È ormai diventato abituale designare questo vasto campo della conoscenza col termine di analisi matematica. Il calcolo ne è ancora il nucleo e lo strumento fondamentale e tuttavia, sin dall'inizio del secolo scorso, nuove idee matematiche ne hanno ampliato le finalità e accresciuto la potenza. Ciò costituisce quello che si chiama comunemente analisi funzionale; si può dire, in prima approssimazione, che essa consiste in un trasferimento all'analisi di concetti e metodi che hanno la loro origine nell'algebra astratta (intesa secondo la concezione sviluppatasi a partire dalla metà del XIX sec.), nella geometria classica e nella topologia.

Questa processo cominciò a prender corpo tra la fine del XIX e l'inizio del XX sec. con lo studio di spazi funzionali a infinite dimensioni. Dopo i pionieristici lavori di Vito Volterra e Ivar Fredholm sulle equazioni integrali, David Hilbert affrontò il problema degli autovalori di equazioni integrali a nucleo simmetrico e, più in generale, lo sviluppo della teoria delle forme quadratiche infinite limitate. Questi lavori di Hilbert si combinarono con la contemporanea definizione dell'integrale di Lebesgue e l'introduzione di concetti geometrici e topologici in analisi da parte di Maurice Fréchet. Progressi che consentirono di tradurre i risultati di Hilbert nel linguaggio di quelli che oggi si chiamano appunto spazi di Hilbert, che collegano la geometria alla teoria dell'integrazione rendendo possibile lo studio dei più generali sistemi di equazioni lineari in tali spazi.

Un passo decisivo nello sviluppo dell'analisi fu compiuto nel 1922 da Stefan Banach con la creazione della teoria degli operatori lineari in spazi lineari, normati e completi rispetto alla norma, i cosiddetti spazi di Banach. Per esempio, se si considera un insieme X qualsiasi e l'insieme di tutte le funzioni reali su esso definite, si ottiene uno spazio vettoriale topologico introducendo in esso un'opportuna topologia prodotto. Se si prende il sottospazio delle funzioni limitate si ottiene uno spazio vettoriale che può essere dotato di una topologia completamente differente, introducendo la norma dell'estremo superiore, e ottenendo così uno spazio di Banach rispetto a essa. Questi risultati si possono opportunamente generalizzare, per esempio prendendo in considerazione, invece che funzioni a valori reali, funzioni a valori in uno spazio di Banach e così via.

Come risultato di questi sviluppi oggi è naturale pensare gli oggetti dell'analisi matematica ‒ cioè le funzioni, gli operatori eccetera ‒ come 'punti' di certi spazi astratti, nei quali sia possibile definire, da una parte, concetti topologici come quelli di limite, continuità, intorno, eccetera e, dall'altra, strutture algebrico-geometriche come gruppi, spazi vettoriali, applicazioni lineari, anelli e così via. È del tutto corretto, naturalmente, affermare che l'analisi matematica ha sempre fatto il più ampio uso dei metodi algebrici e che essa ha sempre avuto come fondamento il concetto di limite; tuttavia, apparirà ben presto chiaro al lettore che lo spirito secondo cui algebra e topologia vengono impiegate e combinate nella moderna analisi funzionale è molto diverso da quello delle applicazioni classiche.

Ritorno al calcolo infinitesimale

Contrariamente al trattamento classico, nelle concezioni attuali le funzioni reali di una variabile reale non costituiscono più un capitolo speciale e introduttivo, ma intervengono solo di tanto in tanto svolgendo un ruolo puramente strumentale. Per sviluppare la teoria si introducono due spazi di dimensione finita ℝ^m e ℝⁿ, la topologia dei quali viene opportunamente definita mediante norme (è noto che due distinte norme su ℝⁿ sono sempre equivalenti e definiscono la stessa topologia). Si considerano poi le funzioni definite in un sottoinsieme aperto U di ℝ^m, a valori in ℝⁿ; due qualsiasi di tali funzioni f e g, continue in un punto x₀∈U, si dicono tangenti in quel punto se risulta f(x₀)=g(x₀) e se il rapporto ∥f(x)∥/∥x−x₀∥ tende a 0 quando x tende ad x₀ in U−{x₀}. Si dimostra facilmente che due funzioni affini x→a+u(x−x₀), x→b+v(x−x₀) (dove a, b appartengono ad ℝⁿ ed u e v sono applicazioni lineari da ℝ^m a ℝⁿ) possono essere tangenti in x⁰ soltanto quando esse coincidono. Ne segue che una sola, al più, di tali funzioni x→f(x₀)+u(x−x₀) può essere tangente ad f in x₀; in questo caso, si dice che f è differenziabile in x₀, l'applicazione lineare u∈ℒ(ℝ^m;ℝⁿ) si chiama la sua derivata (totale) in x₀ e si scrive Df(x₀): a ciascun vettore h∈ℝ^m resta così associato un vettore di ℝⁿ che si può indicare con Df(x₀)∙h. Quando la derivata esiste in ogni punto di U, essa definisce un'applicazione x→Df(x) da U ad ℒ(ℝ^m;ℝⁿ) (e non da U ad ℝⁿ) che si chiama la derivata di f in U. È soltanto nel caso in cui m=1 che ℒ(ℝ;ℝⁿ) può essere identificato canonicamente con ℝⁿ, e quindi l'applicazione lineare t→a∙t può essere a sua volta identificata con il vettore a; con tali identificazioni si è ricondotti al concetto classico secondo cui la derivata di f in x₀ è un vettore di ℝⁿ (oppure un numero se risulta anche n=1). La derivata Df(x₀) va così riguardata come la migliore approssimazione lineare di x→f(x)−f(x₀) nell'intorno di x₀; questa nuova concezione rende pressoché ovvie, esprimendole nel linguaggio precedente, le regole formali del calcolo differenziale.

La presentazione del calcolo che ne consegue è non soltanto molto più naturale e intrinseca rispetto a quella classica, ma ha anche il vantaggio di adattarsi automaticamente quando si sostituiscano gli spazi ℝⁿ con spazi di Banach arbitrari. I recenti sviluppi nella teoria delle varietà di Banach, che hanno già condotto ad importanti risultati in parecchi problemi classici, sono interamente fondati sul suddetto vantaggio.

I più importanti spazi funzionali

Dato un insieme X qualsiasi, l'insieme di tutte le funzioni reali definite in X (cioè di tutte le applicazioni da X in ℝ) è il prodotto cartesiano ℝ^X; a ogni x∈X corrisponde una proiezione nello spazio coordinato ℝ_x, che assegna a ogni funzione il suo valore in x (funzione di valutazione): f →f(x). ℝ^X può essere riguardato come uno spazio vettoriale topologico se si introduce in esso la topologia prodotto; affinché una successione di funzioni (f_n) converga a una funzione f secondo tale topologia, è necessario e sufficiente che, per ogni x∈X, la successione di numeri (f_n(x)) converga a f(x) in ℝ: questo tipo di convergenza si chiama puntuale.

Consideriamo ora in ℝ^X il sottoinsieme ℬ(X) delle funzioni f che sono limitate, per le quali cioè esista un numero M (finito e dipendente dalla funzione) tale che ∣f(x)∣≤M per ogni x∈X. È immediato constatare che si tratta di un sottospazio vettoriale di ℝ^X al quale, tuttavia, può anche essere assegnata una topologia completamente differente: per ogni f∈ℬ(X), sia ∥f∥ l'estremo superiore dell'insieme X di tutti i valori assoluti ∣f(x)∣ per ogni x∈X. Allora ∥f∥ è una norma su ℬ(X), e ℬ(X) è uno spazio di Banach per tale norma. Affinché una successione (f_n) di funzioni f_n in ℬ(X) converga a una funzione f nella topologia indotta dalla suddetta norma, è necessario e sufficiente che, per ogni ε>0, esista un n₀, dipendente soltanto da ε tale che, per ogni x∈X, la disuguaglianza n≥n₀ implichi l'altra: ∣f_n(x)−f(x)∣≤ε; questo tipo di convergenza si chiama convergenza uniforme in X; essa implica naturalmente la convergenza puntuale, ma il viceversa è falso se l'insieme X ha cardinalità infinita. Lo spazio di Banach ℬ(X) è separabile se e solo se X è finito.

Supponiamo ora che l'insieme X sia esso stesso uno spazio topologico; possiamo allora definire in ℬ(X) il sottospazio ℬ^∞(X) di tutte le funzioni continue e limitate (se X è compatto coincide con l'intero spazio C(X) delle funzioni continue, mentre ‒ più in generale ‒ si ha C^∞(X)=ℬ(X)∩C(X)). C^∞(X) è un sottospazio vettoriale chiuso di ℬ(X) (cioè, in altre parole, una successione uniformemente convergente di funzioni continue e limitate ha una funzione continua come limite). Lo spazio C^∞(X), dotato della norma indotta da quella di ℬ(X), è pertanto uno spazio di Banach; quando X è compatto e metrizzabile, tale spazio di Banach (che in questo caso, come già detto, coincide con C(X)), è separabile.

Nelle precedenti definizioni, ℝ può essere sostituito da uno spazio di Banach F, e la definizione di ∥f∥ diventa allora

[1] formula;

i risultati sono gli stessi (per quanto riguarda la separabilità, F dev'essere separabile) e i relativi spazi si indicano rispettivamente con ℬ_F(X), C_F^∞(X) e C_F(X). Nei casi in cui F=ℝ oppure F=ℂ, gli spazi ℬ_ℝ(X) e ℬ_ℂ(X) sono algebre di Banach rispetto all'ordinaria moltiplicazione fra funzioni, poiché risulta ∥fg∥≤∥f∥∙∥g∥ e la norma di una funzione costante uguale a λ è ∣λ∣; C^∞(X) e C^∞_ℂ(X) sono, rispettivamente, sottoalgebre di ℬ(X) e ℬ_ℂ(X). Le algebre C(X) e C_ℂ(X) diventano particolarmente importanti quando lo spazio X è compatto; in tal caso, esiste una corrispondenza biunivoca tra i sottoinsiemi chiusi di X e gli ideali chiusi di C(X), che associa a ogni sottoinsieme chiuso F di X l'ideale a(F) di tutte le funzioni che sono 0 in F; il medesimo risultato vale anche per C_ℂ(X). I punti di X, in particolare, sono in corrispondenza biunivoca con gli ideali massimali di C(X) o di C_ℂ(X). Inoltre, vi è una notevole caratterizzazione delle sottoalgebre di C(X) che contengono l'elemento unitario 1 e che sono dense in C(X); esse sono quelle sottoalgebre A che separano i punti di X, e cioè per ogni coppia di punti distinti x,y di X esiste una f∈A tale che f(x)≠f(y) (teorema di Stone-Weierstrass). Prendendo come spazio X l'intervallo chiuso [0,1], si ottiene come caso particolare il classico teorema di approssimazione di Karl T. Weierstrass se si sceglie come sotto-algebra A quella dei polinomi reali. Nel caso di C_ℂ(X), invece, non vale alcuna analoga caratterizzazione: si deve richiedere in più che f∈A implichi f-∈A ovvero, in altre parole, che A sia stabile per il coniugio fra numeri complessi. Nel caso in cui X sia il cerchio unitario ∣z∣=1 in ℂ, si ottiene il teorema di approssimazione di Weierstrass per i polinomi trigonometrici.

Se X non è compatto, bensì localmente compatto, ed è l'unione di tutti i termini di una successione crescente di sottoinsiemi compatti K_n ‒ cioè tale che ciascun K_n è contenuto nell'interno di K_n+1 come per esempio un sottoinsieme aperto di un sottoinsieme chiuso e illimitato di un ℝ^p ‒ allora una delle topologie più utili nello spazio C(X) di tutte le funzioni reali continue su X è quella della convergenza compatta: essa viene definita mediante una successione crescente di seminorme

[2] formula

e affinché una successione (f_v) di funzioni continue converga a f con tale topologia è necessario e sufficiente che f_ν(x) converga uniformemente a f(x) in ogni sottoinsieme compatto di X (e ciò non implica affatto che f_ν converga uniformemente in tutto lo spazio X). Lo spazio vettoriale topologico così ottenuto non è più uno spazio di Banach bensì uno spazio di Fréchet; è uno spazio separabile quando X è metrizzabile e separabile.

I sottoinsiemi compatti dello spazio C(X) dotato della suddetta topologia (per X localmente compatto) sono collegati a un'importante proprietà degli insiemi di funzioni continue: uno di tali insiemi, sia H, si dice equicontinuo nel punto x₀ se, comunque scelto ε>0, esiste un intorno V di x₀ tale che per tutte le funzioni f∈H la relazione x∈V implica ∣f(x)−f(x₀)∣≤ε. Un insieme H si chiama equicontinuo se è equicontinuo in ogni punto di X. Se X, per esempio, è un insieme aperto di ℝⁿ, se le funzioni appartenenti ad H sono tutte differenziabili e se per ogni x∈X esistono un intorno V di x in X e un numero M>0 tali che per tutte le funzioni f ∈H risulti ∥Df(y)∥≤M per ogni y∈V, allora H è equicontinuo. Ora, il teorema di Ascoli stabilisce che un sottoinsieme H⊂C(X) è relativamente compatto in C(X) se e solo se sono soddisfatte le due condizioni seguenti: (a) H è equicontinuo; (b) esiste un sottoinsieme denso D di X tale che, per ogni x∈D, l'insieme H(x) composto da tutti i numeri f(x) per f ∈H sia limitato.

Le definizioni e i risultati precedenti possono essere facilmente generalizzati se si prendono in considerazione, anziché funzioni a valori reali, funzioni a valori in uno spazio ℝ^m o addirittura in uno spazio di Banach.

Se X è un sottoinsieme aperto di ℝⁿ, si può definire in modo analogo tutto un sistema di spazi di Fréchet separabili prendendo in considerazione soltanto le funzioni differenziabili: per qualsiasi r>0, C^(r)(X) è lo spazio vettoriale di tutte le funzioni r-volte differenziabili con derivata continua in X; si definisce allora la topologia su C^(r)(X) mediante la successione crescente di seminorme

[3] formula

ove p_n è la norma definita sopra. Questa topologia ha la proprietà (che non è condivisa dagli spazi E^(r)(X)) che un sottoinsieme H di E(X) è relativamente compatto non appena esso è limitato, e cioè tale che ogni seminorma p_n,r è limitata in H.

Un terzo tipo di importanti spazi funzionali proviene dalla teoria dell'integrazione. Sia p un numero reale qualsiasi tale che 1≤p〈+∞; per ogni funzione reale definita e misurabile secondo Lebesgue nell'intervallo [0,1], e tale che l'integrale ∫¹₀∣f(x)∣^p dx sia finito, poniamo

[4] formula.

Dalla disuguaglianza di Minkowski segue allora che l'insieme ℒ^p([0,1]) di queste funzioni è uno spazio vettoriale reale e che N_p è una seminorma in tale spazio. Tuttavia, N_p non è una norma poiché N_p(f)=0 per tutte le funzioni che sono quasi ovunque nulle. Per poter ottenere una norma è necessario identificare tutte le funzioni di ℒ^p([0,1]) che sono fra loro uguali quasi ovunquee, se f∼ è una tale classe, porre N_p(f∼)=N_p(f) per ogni funzione della classe f∼; allora l'insieme L^p([0,1]) di queste classi d'equivalenza è uno spazio vettoriale e N_p è una norma su tale spazio. Inoltre, si può dimostrare che L^p([0,1]) è completo per tale norma, cioè che è uno spazio di Banach.

Per p=−∞, si definisce uno spazio ℒ^∞([0,1]) nel modo seguente: esso consiste delle funzioni f misurabili secondo Lebesgue e che sono essenzialmente limitate (per le quali, cioè, esiste un numero finito M tale che ∣f(x)∣≤M quasi ovunque). Questo è ancora uno spazio vettorialee, se N_∞(f) è il più piccolo numero M che gode della proprietà precedente, allora N_∞ è una seminorma su ℒ^∞([0,1]). Identificando di nuovo le funzioni che sono fra loro quasi ovunque uguali, si ottiene uno spazio vettoriale L^∞([0,1]) dotato di una norma che lo rende ancora uno spazio di Banach.

Le definizioni precedenti si possono generalizzare sostituendo [0,1] con un qualsiasi spazio topologico X localmente compatto e la misura di Lebesgue con una misura di Radon positiva μ su X; si ottengono così gli spazi di Banach L^p(X,μ), (1≤p≤+∞); se X è metrizzabilee separabile, questi spazi sono separabili ‒ ad eccezione di L^∞(X,μ) ‒ e il sottospazio ✄∼(X) composto dalle classi di funzioni continue a supporto compatto è denso in L^p(X,μ), di nuovo con l'eccezione di L^∞(X,μ). Si possono anche sostituire le funzioni a valori reali con funzioni a valori complessi, ottenendo così gli spazi di Banach L^p_ℂ(X,μ)=L^p(X,μ)⊕iL^p(X,μ), che godono di proprietà analoghe.

Siano p,q due numeri, entrambi maggiori o uguali a1, che soddisfino la relazione (1/p)+(1/q)=1 (se p=1 si prende q=+∞). Allora, per ogni funzione f∈ℒ^p_ℂ(X,μ) e per ogni funzione g∈ℒ^q_ℂ(X,μ) il prodotto fg è integrabile per μ e si ha (disuguaglianza di Hölder)

[5] N₁(fg)≤N_p(f)N_q(g).

Ciò implica che il duale dello spazio di Banach L^p_ℂ(X,μ) è L^q_ℂ(X,μ) per 1≤p〈+∞; gli spazi L^p_ℂ(X,μ) sono pertanto riflessivi ad eccezione di L¹_ℂ(X,μ) e di L^∞_ℂ(X,μ).

Lo spazio L²_ℂ(X,μ) è particolarmente importante perché esso è uno spazio di Hilbert se si definisce il prodotto scalare di due classi f∼, g∼ ponendo

[6] formula.

La norma N₂ su tale spazio è così (f∼∣f∼)^1/2.

Casi notevoli di spazi L^p(X,μ) si ottengono prendendo come insieme X quello, ℕ, dei numeri naturali (o più generalmente qualsiasi spazio discreto numerabile) e come misura μ quella di massa +1 concentrata in ciascun punto di ℕ. Si scrive allora l^p ed l^p_ℂ in luogo di L^p(ℕ,μ) e, rispettivamente, L^p_ℂ(ℕ,μ); così, per 1≤p〈+∞, l^p_ℂ è lo spazio di tutte le successioni complesse x=(ξ_n) tali che

[7] formula;

l^∞_ℂ è lo spazio di tutte le successioni complesse e limitate x=(ξ_n), con

[8] N_∞(x)=sup_n(∣ξ_n∣).

Per tutti gli spazi X separabili, localmente compatti e metrizzabili, lo spazio di Hilbert L²_ℂ(X,μ) o ha dimensione finita oppure è isomorfo a l²_ℂ; tale spazio risulta così dotato di una base di Hilbert (φ∼_n) che consiste delle classi di funzioni φ_n tali che

[9] formula

e ogni funzione f∈ℒ²_ℂ(X,μ) può essere espressa come una serie ∑_nc_nφ_n, con c_n=(f∼∣φ∼_n). Questa serie converge a f nello spazio topologico ℒ²_ℂ(X,μ), mentre per un assegnato x∈X la serie ∑_nc_nφ_n(x) non sarà necessariamente convergente. Gli esempi più importanti sono, per L²([0,1]), il sistema ortonormale (e^2nπix) e, per L²(ℝ), le funzioni di Hermite

[10] formula.

Va osservato che per p≠2 non esistono analoghe relazioni tra l^p ed L^p.

Teoria spettrale

Un sistema di n equazioni lineari in n incognite, dove sia i coefficienti che le variabili sono numeri complessi, può essere scritto come

[11] formula

dove x e y sono vettori in uno spazio E n-dimensionale su ℂ e U è un endomorfismo di E (corrispondente a una matrice n×n se si sceglie una base di E). Lo studio di tale equazione conduce a considerare lo spettro di U, e cioè l'insieme dei numeri complessi λ tali che U−λI (dove I è l'automorfismo identico) non sia invertibile. Ciò significa che det(U−λI)=0 e questa è un'equazione algebrica in λ di grado n, che ha quindi almeno una radice e al più n radici. Le radici distinte di tale equazione si chiamano gli autovalori di U e costituiscono lo spettro S=Sp(U). Per ciascun λ∈S sia N(λ), o N(λ,U), il sottospazio di E costituito dai vettori x tali che, per qualche intero m>0, si abbia (U−λI)^m∙x=0. Allora E è la somma diretta dei sottospazi N(λ,U). Infatti, per ogni μ∈S, U−μI è invertibile e d'altra parte, per λ∈S, la restrizione di U−λI alla somma diretta F(λ,U) di tutti i sottospazi N(μ,U) per μ≠λ è invertibile, mentre la sua restrizione a N(λ,U) è nilpotente. Per la funzione razionale di λ∈ℂ, a valori nell'algebra di Banach End(E) di dimensione n², si può scrivere

[12] formula

dove λ_j (con 1≤j≤r) sono gli autovalori distinti, ν_j è la molteplicità di λ_j, le A_jk sono elementi di End(E) e, infine, ∑^r_j=1 ν_j=n. Allora, le condizioni affinché l'equazione (U−λ_j∙I)∙x=y abbia una soluzione x sono le seguenti:

[13] A_{j νj}∙y=0.

Le equazioni funzionali lineari sono, per definizione, quelle che possono essere scritte nella forma [11], in cui la funzione nota y è un elemento di qualche spazio funzionale E, la soluzione x viene cercata nel medesimo spazio E, e U è un'applicazione lineare di E in se stesso. Dire che l'equazione ha una soluzione unica per ogni y∈E, significa che U è una corrispondenza biunivoca (o bigezione) tra E ed E stesso o, equivalentemente, che U è invertibile in End(E). Si è così condotti a ricercare per quali valori di λ∈ℂ l'elemento U−λI sia invertibile; tali valori si chiamano regolari. Il complementare dell'insieme dei valori regolari, Sp(U), si continua a chiamare lo spettro di U. Nessuna teoria delle equazioni funzionali lineari sarebbe possibile senza porre delle ipotesi piuttosto forti per lo spazio E e per l'operatore U; con ipotesi troppo generali, non si riuscirebbe nemmeno a stabilire se lo spettro sia vuoto o coincida con l'intero piano complesso. La proposizione più generale che si può formulare riguarda il caso in cui E è uno spazio di Banach (su ℂ) e U è continuo. Allora, lo spettro Sp(U) è compatto e non vuoto. Ciò segue dall'osservazione che se ∥U∥〈1 allora, nell'algebra di Banach ℒ(E) degli endomorfismi continui diE, I−U è invertibile e (I−U)⁻¹=I+U+U²+…+Uⁿ+… mentre la serie è assolutamente convergente graziealla relazione ∥Uⁿ∥≤∥U∥ⁿ. Da ciò segue che, per ogni U∈ℒ(E), U−ζI=−ζ(I−ζ⁻¹U) è invertibile per ∣ζ∣>∥U∥ e che se U−ζ₀I è invertibile lo è pure U−ζI=(U−ζ₀I)(I−(ζ−ζ₀)(U−ζ₀I))⁻¹ per ∣ζ−ζ₀∣ abbastanza piccolo. In altre parole, il complementare dello spettro in ℂ è aperto e la funzione ζ→(U−ζI)⁻¹ è olomorfa in tale insieme; inoltre, lo spettro è limitato e quindi compatto. Infine, se lo spettro fosse vuoto la funzione (U−ζI)⁻¹ sarebbe olomorfa nell'intero piano e quindi, poiché ∥(U−ζI)⁻¹∥≤C/∣ζ∣ per qualche costante C con ∣ζ∣ abbastanza grande, il teorema di Liouville (applicabile per le funzioni olomorfe a valori in spazi di Banach) implicherebbe che U−ζI sia costante, il che è assurdo.

Si può dimostrare che non è possibile ottenere un risultato migliore nel caso generale, cioè che ogni sottoinsieme compatto di ℂ è lo spettro di qualche operatore continuo U. Inoltre, al contrario di quanto si verifica nel caso a dimensione finita, un elemento ζ∈Sp(U) non è necessariamente un autovalore di U; in altre parole, sebbene U−ζI non sia invertibile, il suo nucleo può essere ridotto a 0 e ciò, per il teorema del grafico chiuso, può accadere soltanto se l'immagine di U−ζI è diversa da E.

Per poter ottenere risultati più precisi si devono fare ipotesi più restrittive sull'operatore U. La teoria più semplice riguarda il caso degli operatori compatti, le cui proprietà sono le più vicine a quelle che si hanno nel caso a dimensione finita.

La teoria di Riesz-Fredholm degli operatori compatti

Sia E uno spazio normato su ℂ (non necessariamente uno spazio di Banach). Un operatore lineare U in E si dice compatto (o completamente continuo) se fa corrispondere a ogni sottoinsieme limitato di E un sottoinsieme relativamente compatto di E (ciò implica che U sia continuo). Allo stesso modo in cui gli insiemi compatti possono essere pensati come a dimensione quasi finita, si può pensare che le applicazioni compatte comprimano lo spazio E fino a ridurlo a un sottospazio di dimensione quasi finita; in particolare, l'applicazione identica (o identità) I non è mai compatta quando E è di dimensione infinita (come stabilisce il teorema di Frigyes Riesz, che è lo strumento fondamentale della teoria degli operatori compatti). Dunque, quando ζ≠0 e U è compatto, U−ζI si presenta come una perturbazione di −ζI, che non dovrebbe essere molto diversa da −ζI stesso salvo nel caso degli spazi a dimensione finita. È su questa idea che si fonda l'intera teoria spettrale degli operatori compatti.

Gli esempi più importanti di operatori compatti sono forniti dagli operatori che hanno immagine a dimensione finita e dai classici operatori di Fredholm nella teoria delle equazioni integrali: supponiamo per esempio che K(x,y) sia una funzione complessa continua in [0,1]×[0,1] (funzione nucleo) e, per ogni f∈C([0,1]), sia U∙f la funzione

[14] formula

che appartiene a C([0,1]); allora U è un operatore compatto.

Il teorema fondamentale della teoria di Riesz-Fredholm è il seguente: se U è un operatore compatto, e se V=I−U, allora il nucleo Ker(V) ha dimensione finita, l'immagine Im(V) ha codimensione finita ed è chiusa in E, e si ha

[15] codim(Im(V))=dim(Ker(V)).

Applicando il teorema di Riesz-Fredholm, è abbastanza facile ottenere i seguenti risultati sullo spettro di un operatore compatto U.

Lo spettro Sp(U) di un operatore compatto U è un sottoinsieme al più numerabile di ℂ; contiene sempre lo 0 se E ha dimensione infinita; tutti i punti λ≠0 nello Sp(U) sono punti isolati di tale insieme e sono autovalori di U. Per ciascuno di tali autovalori λ si definisce il sottospazio N(λ) di E come l'insieme di tutti gli x∈E per i quali esiste un intero m>0 tale che (U−λI)^m∙x=0. Allora N(λ) ha dimensione finita ed esiste un intero minimo k=k(λ) tale che la restrizione di (U−λI)^k a N(λ) è 0. L'immagine F(λ) mediante (U−λI)^k di E è allora un sottospazio chiuso di E, complementare di N(λ), e la restrizione di U−λI a F(λ) è una bigezione di tale spazio con se stesso. Per tutti i μ≠λ in Sp(U) si ha N(μ)⊂F(λ). Infine, se E è uno spazio di Banach, (U−ζI)⁻¹ è una funzione meromorfa di ζ nel complementare di {0}, che presenta un polo k(λ) in ciascun punto λ≠0 di Sp(U).

Nel caso in cui E è uno spazio di Hilbert, ogni operatore continuo U in E è dotato di un operatore aggiunto U*, che è definito dalla relazione

[16] (U∙x∣y)=(x∣U*∙y)

e che è continuo. Si ha (U*)*=U, ∥U*∥=∥U∥, (U+V)*=U*+V*, (λU)*=λ-U* per ogni scalare complesso λ, (UV)*=V*U*. Quando U è compatto, U* esiste sempre ed è anch'esso compatto. Lo spettro Sp(U*) è allora l'immagine di Sp(U) mediante il coniugio ζ→ζ- e k(λ,U)=k(λ-,U*); N(λ,U) ed N(λ,U*) hanno la stessa dimensione ed F(λ,U) è il complemento ortogonale di N(λ-,U*); inoltre, se E(λ,U) è l'autospazio di U per l'autovalore λ (cioè l'insieme di tutti gli x tali che U∙x=λx), allora E(λ,U) ed E(λ-,U*) hanno la stessa dimensione. Si ha, in più, il seguente teorema dell'alternativa di Fredholm per le soluzioni di (U−λI)∙x=y per λ≠0: o esiste un'unica soluzione per ogni y∈E, oppure l'equazione (U−λI)∙x=0 ha almeno una soluzione non banale, cosicché una condizione necessaria e sufficiente affinché l'equazione (U−λI)∙x=y abbia almeno una soluzione è che y sia ortogonale a tutte le soluzioni di (U*−λ-I)∙x=0.

Questo è tutto ciò che si può dire in generale per operatori compatti arbitrari; perfino in uno spazio di Hilbert, lo spettro può consistere di qualsiasi successione (λ_n) tendente a 0. Questo spettro può anche ridursi a 0, il che accade sempre per l'equazione integrale di Volterra di seconda specie

[17] formula

in cui l'operatore ha la forma [14] e la funzione K(x,y) si annulla per x〈y. In generale, sebbene la funzione (ζU−I)⁻¹ sia meromorfa nell'intero piano complesso, non esiste una sua semplice espressione corrispondente alla [12]. Quando la serie delle λ_n (contate con la loro molteplicità, la molteplicità di λ essendo la dimensione dell'autospazio E(λ,U)) è assolutamente convergente, allora è possibile definire il determinante di U−ζI per ζ≠0, che è una funzione olomorfa per ζ≠0, ed è possibile scrivere (U−ζI)⁻¹ come un quoziente di due tali determinanti infiniti. Si è così ricondotti alla soluzione originaria di Fredholm della [17] per l'operatore definito da una funzione nucleo continua del tipo [14].

Operatori compatti autoaggiunti

La teoria di Riesz-Fredholm si semplifica molto quando l'operatore compatto U è definito in uno spazio di Hilbert E ed è, inoltre, autoaggiunto, cioè U*=U. Allora: 1) lo spettro Sp(U) è costituito da numeri reali λ_n, e k(λ_n)=1 per ogni autovalore; inoltre, 0 è pure un autovalore (che può essere di molteplicità infinita). Infine, Sp(U) non si riduce a 0 se U non è 0; 2) E è la somma di Hilbert di tutti gli autospazi E(λ_n,U), per λ_n distinti, ed E(0,U); 3) l'operatore (U−ζI)⁻¹ si può scrivere nella forma [12], e cioè

[18] formula

dove P_n è la proiezione ortogonale su E(λ_n,U), purché sia E(0,U)={0}.

La condizione per l'esistenza di una soluzione di (U−λ_n∙I)∙x=y è allora che risulti P_n∙y=0. Ma si possono anche dare condizioni necessarie e sufficienti per l'esistenza di una soluzione di U∙x=y (corrispondente alle equazioni integrali di prima specie per l'operatore [14]): se y_n=P_n∙y, la serie ∑_n(∥y_n∥²/λ_n) dev'essere convergente, e ∑_ny_n/λ_n è una soluzione in E.

L'operatore di Fredholm U definito da una funzione nucleo continua K(x,y) è autoaggiunto se K(y,x)=_____K(x,y). Sia (λ_n) la successione degli inversi degli elementi di Sp(U) diversi da 0, contati con le loro molteplicità; per ogni n, sia φ_n un'autofunzione per λ_n, cioè tale che

[19] formula

che possiamo sempre supporre costituisca un sistema ortonormale in L²([0,1]). L'equazione [19] può essere scritta φ_n(x)____=λ_n(K(x, .)∣φ_n) e dalla disuguaglianza di Bessel per i sistemi ortonormali si ha pertanto

[20] formula

da cui, per integrazione, si ottiene

1

[21] formula

La soluzione dell'equazione integrale [17] in tal caso, per λ distinto da λ_n, può essere scritta mediante le componenti (g∣φ_n)=∫¹₀g(x)φ_n(x)dx rispetto al sistema ortonormale (φ_n):

[22] formula

ove la serie al secondo membro è assolutamente e uniformemente convergente in [0,1].

I risultati precedenti si possono facilmente estendere quando l'intervallo [0,1] è sostituito da un arbitrario spazio compatto X, la misura di Lebesgue da una qualsiasi misura positiva μ su X e K da una funzione che sia a quadrato sommabile su X×X rispetto alla misura prodotto μⓧμ.

Teoria di Hilbert degli operatori autoaggiunti limitati

Sia H un operatore autoaggiunto limitato in uno spazio di Hilbert complesso E. Allora, nell'algebra di Banach ℒ(E) di tutti gli operatori limitati, la sottoalgebra chiusa generata dall'identità e da H è una C*-algebra commutativa A e quindi, per il teorema di Gel'fand-Neumark, è canonicamente isomorfa all'algebra delle funzioni complesse continue C_ℂ(X) (con involuzione f→f-) in cui X è lo spettro di A; inoltre, l'applicazione χ→χ(H) di X (considerato come spazio dei caratteri di A) in ℂ è un omeomorfismo di X sullo spettro di H, che è un sottoinsieme compatto della retta reale ℝ; si identifica X con questo spettro. L'operatore in A che corrisponde alla funzione continua f∈C_ℂ(X) si denota allora con f(H). Si può decomporre E nella somma di Hilbert di sottospazi E_n, ciascuno dei quali è isomorfo allo spazio L²_ℂ(X,μ_n) ‒ μ_n è una misura positiva su X ‒ ed è stabile rispetto ad H. L'azione di H in E_n consiste nel moltiplicare la classe di una funzione g∈ℒ²_ℂ(X,μ_n) per la classe della funzione (limitata) x→x. Questa è la generalizzazione completa del caso classico in cui E ha dimensione finita, X è un insieme finito di numeri reali, E è la somma di Hilbert dei sottospazi unidimensionali E_n, la misura μ_n ha massa 1 in uno dei punti λ_n di X e 0 negli altri e la restrizione di H a E_n è la moltiplicazione per lo scalare λ_n. L'isomorfismo fra E e la somma di Hilbert degli L²_ℂ(X,μ_n) si può chiamare l'isomorfismo diagonalizzante.

Gli autovalori di H sono i punti di X che hanno misura positiva per una delle misure μ_n. Più generalmente, si può definire f(H) per ciascuna funzione reale di Borel limitata su X: in ogni sottospazio E_n, la restrizione di f(H) è la moltiplicazione della classe di una funzione di ℒ²_ℂ(X,μ_n) per la classe della funzione f.

Operatori non limitati in uno spazio di Hilbert

Uno dei maggiori pregi della teoria di Hilbert è che essa consente di prendere in considerazione anche i cosiddetti operatori illimitati in uno spazio di Hilbert, la situazione cioè che si incontra più frequentemente nelle applicazioni ai problemi sulle equazioni differenziali ordinarie o alle derivate parziali. Un operatore illimitato T in uno spazio di Hilbert E non è definito nell'intero spazio E ma soltanto in un sottospazio vettoriale dom(T), che per semplicità supponiamo sia denso in E. Tale operatore è lineare e ha valori in E; non è richiesta la sua continuità nel dom(T) bensì una condizione più debole, e cioè che il grafico Γ(T) in E×E sia chiuso in tale spazio (anche se dom(T) non è chiuso). Si dice allora che T è un operatore chiuso. Una condizione ancor più debole è che T possa essere esteso a un operatore chiuso T₁ definito in un dominio più ampio. Questa condizione può anche essere espressa in altro modo, introducendo per l'operatore T definito in un sottospazio denso dom(T) il concetto di operatore aggiunto. Si consideri in E il sottoinsieme F di tutti i vettori y tali che la forma lineare x→(T∙x∣y) sia continua in dom(T); tale forma può allora essere estesa per continuità a E, e quindi può essere scritta x→(x∣T*∙y) per un unico vettore T*∙y; T*, che è definito in F, è sempre un operatore chiuso, e il suo grafico Γ(T*) può essere facilmente dedotto dal grafico di T: per ottenerlo basta prendere il complemento orto-gonale nello spazio prodotto E×E dello spazio che siottiene applicando alla chiusura Γ(T) la rotazione J:(x,y)→(y,−x). Dire che T può essere esteso a un operatore chiuso significa che F=dom(T) è denso in E; esiste allora un più piccolo operatore chiuso che estende T, detto la chiusura di T: è precisamente il secondo aggiunto T**=(T*)*, il suo grafico è la chiusura Γ(T)____ e si ha (T**)*=T*.

Per un operatore chiuso T, si definisce lo spettro Sp(T) nel seguente modo: si dice che ζ∈ℂ è un valore regolare di T se l'applicazione T−ζI di dom(T) in E è iniettiva, se la sua immagine L è densa e se è tale che l'applicazione inversa (T−ζI)⁻¹ di L in E è continua; il teorema del grafico chiuso implica allora che sia L=E. Il complementare dell'insieme dei valori regolari è per definizione lo spettro Sp(T); per ciascun λ∈ Sp(T) ci sono tre possibilità: (a) λ può essere un autovalore di T (cioè l'applicazione T−λI non è iniettiva), e in tal caso si dice che tali valori costituiscono lo spettro discreto di T; (b) l'applicazione T−λI è iniettiva e la sua immagine L è densa in E, ma l'applicazione inversa (T−λI)⁻¹ di L in E non è continua, e in tal caso si dice che tali valori costituiscono lo spettro continuo di T; (c) l'applicazione T−λI è iniettiva ma L non è denso in E, e in tal caso tali valori costituiscono lo spettro residuo di T. Si dimostra che tutti e tre i casi possono di fatto verificarsi; inoltre, Sp(T) è chiuso in ℂ ma può essere vuoto o coincidente con ℂ; nel complementare di Sp(T), ζ→(T−ζI)⁻¹ è olomorfa.

La teoria di Hilbert si estende facilmente a quegli operatori T non limitati che sono autoaggiunti: ciò significa ora che T è chiuso con dominio dom(T) denso e coincide col suo aggiunto, cioè dom(T*)=dom(T) e T*=T in tale spazio. Allora X=Sp(T) è contenuto nella retta reale ℝ (ma può anche coincidere con l'intera retta) e non esiste spettro residuo. Lo spazio E è di nuovo la somma di Hilbert di sottospazi E_n, ciascuno dei quali è contenuto in dom(T), ed è stabile rispetto a T; dom(T) è allora il sottospazio di E che consiste delle x=∑_nx_n con x_n∈E_n tali che ∑_n∥T∙x_n∥²〈+∞. Ciascuno degli E_n è allora isomorfo a uno spazio L²_ℂ(X_n,μ_n), dove X_n è un sottoinsieme limitato di X e μ_n è una misura positiva su X_n, e la restrizione di T a E_n può essere identificata con la moltiplicazione della classe d'equivalenza della funzione g∈ℒ²_ℂ(X_n,μ_n) con la classe d'equivalenza della funzione x→x. Questo isomorfismo fra E e la somma di Hilbert degli L²_ℂ(X_n,μ_n) si può ancora chiamare l'isomorfismo diagonalizzante.

Nelle applicazioni non si incontrano usualmente operatori autoaggiunti, bensì operatori più generali: gli operatori hermitiani.

I metodi diretti nel calcolo delle variazioni

Fin dai suoi esordi, il calcolo delle variazioni è sempre stato la parte dell'analisi classica in cui già si profilava lo spirito della moderna analisi funzionale. Infatti, il tipo di problemi che potevano essere affrontati mediante tale calcolo coinvolgeva un intero insieme A di funzioni che ovviamente non dipendeva da un numero finito di parametri, come per esempio l'insieme di tutte le funzioni differenziabili con derivata continua su un intervallo [a,b] di ℝ con valori assegnati agli estremi; sopra un tale insieme era definita una funzione (o funzionale; nella terminologia tradizionale) come per esempio ∫^b_a F(x,y,y′)dx, della quale si dovevano trovare il massimo o il minimo. L'impostazione classica di Leonhard Euler e Joseph-Louis Lagrange consisteva nell'ammettere per ipotesi l'esistenza nell'insieme A di funzioni che assumessero effettivamente i valori estremali, e nel cercar di ricavare delle caratterizzazioni di tali funzioni restringendo le funzioni ammissibili a un sottoinsieme di A dipendente da un numero finito di parametri, in cui il problema dei valori estremali avrebbe potuto pertanto essere trattato mediante il calcolo ordinario. Un più approfondito studio delle condizioni necessarie e sufficienti affinché una funzione fosse dotata di massimo o minimo condusse inoltre, negli ultimi trent'anni del XIX sec., a una prima versione di concetti topologici applicati a insiemi di funzioni: per esempio fu messo in evidenza il fatto che in uno stesso insieme A si potevano introdurre parecchi concetti differenti di vicinanza, a seconda che ci si limitasse a considerare due funzioni come vicine fra di loro quando la loro differenza era uniformemente piccola, oppure si pretendesse che tanto la loro differenza quanto la differenza delle loro derivate fosse uniformemente piccola.

È durante questo stesso periodo che la validità dell'ipotesi di esistenza in generale di una soluzione nei problemi variazionali fu smentita con successo, in particolare da Weierstrass, il quale mostrò che alcuni problemi molto semplici possono esser privi di soluzioni: per esempio, il problema di trovare nel piano una curva di minima lunghezza congiungente due punti M e N quando si imponga a essa, in più, la condizione di avere una data tangente in M con direzione diversa da quella della retta MN. Si riconobbe così che, per poter applicare i metodi classici, si doveva dimostrare a priori l'esistenza di una soluzione. La vittima più famosa di questa revisione critica fu il principio di Dirichlet.

Soltanto all'inizio del XX sec. Hilbert e Leonida Tonelli, mediante l'introduzione dei cosiddetti metodi diretti nel calcolo delle variazioni, fornirono dimostrazioni di esistenza dei valori estremali per la maggior parte dei problemi classici (e in particolare per il principio di Dirichlet).

Algebre di Banach di funzioni analitiche

Durante i primi trent'anni del XX sec. fu scoperto da matematici come Godfrey H. Hardy, Frigyes e Marcel Riesz, Gábor Szegö e altri, che l'applicazione dei concetti della teoria di Lebesgue alla classica teoria delle funzioni analitiche di una variabile complessa forniva teoremi di un tipo interamente nuovo in quella teoria. Con lo sviluppo della teoria delle algebre di Banach commutative ci si rese conto che questi teoremi (in un certo senso isolati) potevano essere organizzati nel quadro di quella teoria, il che conduce naturalmente a generalizzazioni in molte direzioni.

L'algebra B

Il punto di partenza è lo studio dell'algebra B di tutte le funzioni complesse f che sono definite e continue nel disco chiuso D:∣z∣≤1 in ℂ e analitiche nel disco aperto ∣z∣〈1. Si tratta di una sottoalgebra chiusa dell'algebra di Banach C_ℂ(D) di tutte le funzioni complesse continue in D, e si vede facilmente che lo spettro di B può essere identificato con D stesso; in altre parole, tutti i caratteri di B hanno la forma f →f(z₀), ove z₀∈D.

Misure rappresentative

L'algebra B è isometrica all'algebra delle restrizioni delle funzioni di B al cerchio unitario U:∣z∣=1, come segue dal principio del massimo. La teoria generale sceglie come punto di partenza una sottoalgebra chiusa A dell'algebra di Banach C_ℂ(X) delle funzioni complesse continue definite su uno spazio compatto X; si fa l'ipotesi che A contenga le funzioni costanti e che separi i punti di X, cosicché X si identifica canonicamente con un sottoinsieme chiuso dello spettro di A.

Nell'algebra B, il teorema di Cauchy implica che

[23] formula

per ogni f∈B, e tale uguaglianza si può anche scrivere

[24] formula

dove χ è il carattere f →f(0) su B, X=U e dμ(θ) è la misura di Haar normalizzata (1/2π) dθ su U. In generale, dato un carattere χ su A si dice che μ è una misura rappresentativa per χ se è una misura positiva su X tale che la [24] valga per tutte le funzioni f∈A, il che implica in particolare che μ abbia massa totale 1. Si può dimostrare, mediante il teorema di Hahn-Banach, che per ogni dato carattere χ su A esiste sempre almeno una misura rappresentativa μ per χ.

Per un dato carattere χ può esistere un insieme infinito di misure rappresentative. Una condizione che assicura l'unicità è quella che A sia un'algebra di Dirichlet. Tali algebre sono caratterizzate dalla proprietà che l'insieme delle parti reali Rf delle funzioni di A sia un sottoinsieme denso di C_ℝ(X). Vi sono molti esempi di algebre di Dirichlet non banali (essendo le C_ℂ(X) quelle banali). L'algebra B è un'algebra di Dirichlet.

Sistemi dinamici

In una serie di lavori penetranti e pionieristici, iniziati nel 1881 e proseguiti durante tutta la sua vita di matematico, Henri Poincaré creò la teoria qualitativa delle equazioni differenziali. Egli era talmente in anticipo sulla sua epoca che mancava delle nozioni topologiche che gli avrebbero consentito di sviluppare le sue eccezionali intuizioni in una teoria sistematica. È soltanto negli ultimi quindici anni che questa teoria è stata posta su solide basi come parte dell'analisi funzionale, e che sostanziali progressi sono stati possibili al di là del lavoro di Poincaré.

Un gran numero di sistemi dinamici che hanno origine da problemi di meccanica classica (problema degli n corpi, moto di un solido, geodetiche di una superficie di rivoluzione, ecc.) posseggono integrali primi; si può dimostrare che non sono mai sistemi strutturalmente stabili. Ciononostante, il loro studio ha un grande interesse teorico e pratico, e così pure lo studio di sistemi che sono a essi abbastanza vicini (teoria delle perturbazioni). Anche questo studio fu iniziato da Poincaré e da George Birkhoff, e sono stati fatti importanti progressi da parte di Andreij N. Kolmogoroff, Vladimir I. Arnold e Jürgen Moser.

Bibliografia

Abraham 1967: Abraham, Ralph, Foundations of mechanics, New York-Amsterdam, Benjamin, 1967.

Abraham, Robbin 1967: Abraham, Ralph-Robbins, Joel, Transversal mappings and flows, New York-Amsterdam, Benjamin, 1967.

Arnold, Avez 1967: Arnold, Vladimir I.-Avez, André, Théorie ergodique des systèmes dynamiques, Paris, Gauthier-Villars, 1967.

Browder 1969: Browder, Andrew, Introduction to function algebras, New York-Amsterdam, Benjamin, 1969.

Courant, Hilbert 1913: Courant, Richard-Hilbert, David, Methoden der mathematischen Physik, 2. ed., Berlin, Springer, 1931 (v. I).

Dieudonné 1960-1970: Dieudonné, Jean, Treatise on analysis, New York, Academic Press, 1960-1970.

Dunford, Schwartz 1963: Dunford, Nelson-Schwartz,Jacob T., Linear operators. II. Spectral theory, New YorkInterscience, 1963.

Duren 1970: Duren, Peter L., Theory of Hp spaces, New York Academic Press, 1970.

Gamelin 1969: Gamelin, Theodor, Uniform algebras, Englewood Cliffs, N. J., Prentice-Hall, 1969.

Hoffman 1962: Hoffman, Kenneth, Banach spaces of analytic functions, Englewood Cliffs, N. J., Prentice-Hall, 1962.

Leibowitz 1970: Leibowitz, Gerald M., Lectures on complex function algebras, Glenview Scott, Foresman, 1970.