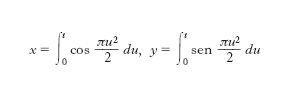clotoide
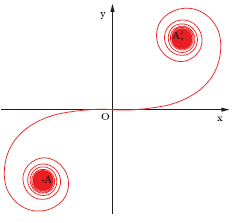
Curva piana (anche detta spirale c.), non algebrica, simmetrica rispetto a un punto O (v. fig.) e dotata di due punti asintotici A e A′ (ai quali cioè la curva si avvicina indefinitamente, con andamento a spirale, senza raggiungerli mai); in ogni punto della c. la curvatura 1/r è proporzionale alla lunghezza dell’arco s, calcolata a partire dall’origine O (r∙s=cost.). Le coordinate di un suo punto possono scriversi, in funzione di un parametro t:
per t che tende a ± ∞ si ottengono, in particolare, le coordinate dei due punti asintotici. La c., introdotta e studiata da G. Bernoulli, interviene, con il nome di spirale di Cornu, nella teoria della diffrazione e ha rilevanza anche in problemi della tecnica: archi di c. rappresentano, per es., il più razionale tipo di raccordo tra un rettifilo e una curva circolare in costruzioni stradali e ferroviarie (➔ raccordo).