Computer science

Computer science

La computer science si colloca con caratteristiche peculiari tra le scienze cosiddette esatte e l’ingegneria, costituendo dal punto di vista accademico un settore giovane. I primi dipartimenti universitari di computer science sono sorti negli anni Sessanta del secolo scorso, e la maggior parte delle più prestigiose università ha definito programmi di studio comprendenti corsi di matematica, fisica e ingegneria elettronica soltanto nei primi anni Settanta. Benché sia considerata scienza piuttosto che ingegneria, la computer science è stata fortemente influenzata dalla rapida crescita dei lavori di programmazione e dalla pratica del calcolo. Quest’ultima è cambiata drasticamente nei sessant’anni che intercorrono tra le prime macchine calcolatrici prodotte durante la Seconda guerra mondiale e i giorni nostri, anche grazie alla potenza crescente e al costo calante degli strumenti messi a disposizione dal rapido progresso tecnologico.

Non bisogna tuttavia dimenticare che anche la storia antica offre esempi di strumenti di calcolo analoghi a quelli moderni, con una funzione ben definita, usualmente impiegati per la navigazione; tra questi vi è il planetario greco, risalente all’80 a.C. circa, rinvenuto in un relitto nei pressi di Anticitera, mediante il quale era possibile calcolare il movimento delle stelle e dei pianeti. Di natura più direttamente legata al calcolo erano invece strumenti come l’abaco (3000 a.C. ca.) e il regolo calcolatore (di cui il primo, le bacchette di John Napier, è del 1610), che potevano essere utilizzati per risolvere problemi di vario genere a seconda dell’input dato.

Il problema dell’immagazzinamento delle informazioni fu affrontato successivamente. Le macchine tabulatrici di Herman Hollerith, create nel 1890, usavano schede perforate per registrare i dati del censimento degli Stati Uniti di quell’anno. Tali schede erano state usate anche precedentemente nel corso dell’Ottocento, ma Hollerith estese questa tecnologia meccanica sviluppandone una versione elettromeccanica nella quale contatti elettrici, attraverso i fori di una scheda, selezionavano combinazioni di condizioni e registravano il numero trovato. Il primo passo verso la matematica digitale era compiuto. Se con il regolo calcolatore la precisione di un numero dipende dalla dimensione della scala sulla quale viene rappresentato e dalla cura con cui è estratto il risultato di una moltiplicazione, in questo caso grandezze espresse sotto forma di numeri si conservano nelle operazioni di copia e nella gran parte delle operazioni aritmetiche. Una situazione ben diversa da quella tipica del mondo dei fenomeni fisici, in cui tutte le operazioni sulle quantità misurate ne riducono inevitabilmente l’accuratezza.

La natura delle macchine calcolatrici ha continuato ad avere un ruolo importante nella scelta e nella definizione dei problemi risolvibili con il computer fino a prima del 1960. Oggi, la computer science interessa campi diversi di attività, dal miglioramento delle metodologie per lo sviluppo di software commerciali al contributo alla ricerca matematica, ampliando la comprensione della struttura della conoscenza e della logica della dimostrazione rigorosa. Motivi di spazio non ci permettono una trattazione completa dell’argomento, che sarà pertanto limitata ai procedimenti di calcolo e ai contesti che hanno stimolato i progressi della computer science, producendo nella nostra comprensione della natura del calcolo una profonda evoluzione. A conclusione dell’articolo si indicheranno alcune ricerche che potrebbero influenzare il modo di utilizzare il computer alla fine del XXI secolo.

Il calcolo prima della computer science (ante 1960): visioni e visionari

L’idea di un calcolo che effettua una qualunque successione di operazioni fu messa a fuoco con la definizione di Alan M. Turing di macchina calcolatrice ideale. La macchina di Turing, puramente concettuale, consiste in un nastro di memoria di lunghezza praticamente infinita, suddiviso in celle lette da una testina. Le celle possono contenere simboli di un alfabeto finito. Le operazioni che la macchina a ogni passo è in grado di compiere consistono nel leggere una cella, scriverci un nuovo simbolo, spostarsi nella cella precedente o successiva e cambiare lo stato interno. Benché nella pratica questo modo di operare fosse poco efficiente, esso realizzava gli obiettivi di Turing. Nel 1936 egli mostrò che la sua macchina era in grado di eseguire qualsiasi calcolo matematico, ma non era capace di portarli tutti a termine. In particolare, la macchina di Turing non poteva risolvere il problema della fermata (halting-problem): dato un programma, questo si fermerà per ogni suo input? Ciò rispondeva all’ultima della famosa serie di domande poste da David Hilbert nel 1928 a proposito della completezza, coerenza e decidibilità della matematica formale.

Turing sarebbe diventato la figura principale nello sforzo britannico, coronato da successo, di decrittazione di codici condotto durante la Seconda guerra mondiale a Bletchley Park, nei dintorni di Londra, che prevedeva l’utilizzazione di nuove macchine calcolatrici per esplorare meccanicamente le implicazioni logiche dell’indovinare o del conoscere parti di un messaggio in codice più lungo.

Dopo la guerra Turing partecipò allo sviluppo delle macchine calcolatrici elettroniche. Nel 1950 introdusse il test di Turing, che può considerarsi una risposta alla domanda: le macchine possono pensare? La sua risposta assume la forma di un gioco: qualora non si possa distinguere se si stia tenendo una conversazione scritta, a distanza, con una persona o con un calcolatore, allora è ragionevole affermare che il computer (se di computer si tratta) stia pensando.

Il primo calcolatore elettronico, prototipo di una macchina più grande mai terminata, è stato costruito nel 1939 da John V. Atanasoff alla Iowa State University. Esso era in grado soltanto di risolvere sistemi di equazioni lineari, impiegando alcune tecnologie che anticipavano i tempi: interruttori a valvola elettronica (vacuum tube switches) e condensatori, usati come bit di memoria che dovevano essere raffreddati per conservare i dati proprio come oggi i chip di memoria dinamica sono raffreddati nei computer. Nel 1941 Konrad Zuse completava a Berlino il primo calcolatore operativo programmabile, lo Z3, basato su relè elettromeccanici. Verso la fine della Seconda guerra mondiale, gli americani iniziarono a progettare calcolatori elettronici, spinti dal loro frequente uso come strumenti di calcolo meccanico intensivo per costruire tavole di parametri balistici e rispondere alle domande poste dallo sviluppo delle armi atomiche. La natura delle intenzioni coinvolte, le invenzioni conseguenti alla segretezza di questi progetti e perfino il fatto che i programmi di vari paesi fossero tenuti segreti agli stessi alleati costituiscono un argomento interessante per gli storici. In ogni caso, la gran parte delle strutture che sono a fondamento dei calcolatori fu gradualmente creata in quel periodo.

Inizialmente queste macchine venivano programmate inserendo cavi in pannelli estraibili o leggendo un programma da codici impressi su un nastro di carta esterno; ma la necessità di memorizzare il programma nel calcolatore divenne presto evidente quando la velocità di calcolo superò la velocità di lettura dei nastri di carta. In diversi contesti fu inventato il ciclo di programma, nel quale una serie di istruzioni viene ripetuta sotto il controllo di un’istruzione di diramazione condizionata, la quale consente l’uscita dal ciclo non appena ottenuto il risultato del calcolo. Inizialmente le subroutine consistevano in processi codificati separatamente su diversi nastri di carta ma inseriti nel programma mediante lettori multipli. Successivamente si sviluppò il concetto di istruzione di salto fra programmi (dal programma chiamante a quello chiamato), con rinvio automatico all’istruzione successiva nel programma chiamante.

La maggior parte delle prime macchine operava con numeri interi, espressi in notazione decimale o binaria, a seconda della macchina. Il primo studio sulla rappresentazione binaria dei numeri si attribuisce a Gottfried Wilhelm Leibniz. Ideato fin dal 1679, fu esposto nella memoria Une nouvelle science des nombres, inviata all’Académie des Sciences di Parigi nel 1701. Carlo XII di Svezia preferiva usare la base 8, ma nel 1697 morì in battaglia prima di poter mettere in atto il suo progetto di imporre ai sudditi l’uso dell’aritmetica ottale. I numeri con una parte frazionaria, come 3,1416, dovevano essere generati indicando, una volta eseguito il calcolo, un fattore di scala per la loro normalizzazione. La rappresen-tazione dei numeri in virgola mobile nell’hardware dei calcolatori apparve per la prima volta nel 1936, nellamacchina incompleta di Zuse. I numeri vi erano rappresentati con due elementi: una mantissa (un numero più piccolo dell’unità espresso in notazione binaria posizionale) e un esponente, che in quella macchina era la potenza di 2 mediante la quale si riscalava (scale up) il numero.

Ciò separa la risoluzione con cui si specifica un numero (il numero di bit della mantissa) dal dominio dinamico del numero stesso. Le unità hardware in virgola mobile nei computer moderni operano direttamente con la notazione scientifica decimale, con la quale si rappresentano i numeri molto grandi o molto piccoli (per es., il numero di Avogadro 6,022×10²³).

Nella scala delle funzionalità di un computer le applicazioni (i programmi che risolvono automaticamente specifici problemi di interesse dell’utente) si trovano a un livello superiore a quello delle istruzioni o, almeno, così era inizialmente; oggi fra i due livelli ci sono molti strati di software di sistema (i programmi, che costituiscono le funzionalità di base del computer, e consentono l’esecuzione delle varie applicazioni). La computer science è nata dall’analisi degli algoritmi (i procedimenti di calcolo ripetuti), adottati nell’esecuzione delle applicazioni di più frequente utilizzazione, e dai processi di sostegno al software di sistema. In particolare, negli anni Cinquanta le applicazioni del calcolo automatico (le cosiddette voci di registro o unit record) che costituivano una pratica largamente diffusa.

Il costo elevato della memoria implicava che la maggior parte dei dati venisse memorizzata su supporti magnetici di basso costo, quali per esempio le bobine di nastro, che consentivano il solo accesso sequenziale (e non diretto) ai dati. Pertanto, tutto ciò che si voleva fare con una parte dei dati poteva avere luogo solo quando se ne disponeva completamente. Il problema dell’ordinamento dei dati venne intensamente studiato, poiché le operazioni di ricerca in un insieme di dati sono possibili e rese agevoli solo quando gli stessi si presentano in un ordine noto.

Con la diffusione dei computer divenne naturale stimare la complessità delle operazioni di calcolo necessarie per l’ordinamento e la ricerca dei dati da parte delle applicazioni più diffuse. La misura fondamentale della complessità è il tempo richiesto per ottenere un risultato, anche se spesso alcune altre grandezze operative possono fornire misure più rilevanti o più facilmente generalizzabili. Si consideri, per esempio, l’ordinamento di grandi quantità di dati in ordine crescente, in modo che possano essere ricercati agevolmente in un secondo tempo. Negli anni Cinquanta del XX sec. tali dati venivano memorizzati su un singolo nastro magnetico. Con una testina magnetica, sia di lettura sia di scrittura, si leggevano due numeri successivi dal nastro, ricopiando il più piccolo su un secondo nastro e conservando il più grande in un registro del computer (un dispositivo di elaborazione che consente di eseguire facilmente le operazioni aritmetiche); poi si leggeva il numero seguente sul primo nastro. Il più piccolo dei due (fra quello letto e quello contenuto nel registro) veniva copiato sul secondo nastro e il più grande memorizzato nel registro per il confronto successivo. In tal modo, quando si raggiungeva la fine del nastro, il registro conteneva il numero più grande dell’insieme dei dati esaminati. Reiterando successivamente questa elaborazione automatica con i due nastri e leggendo sempre dal nastro scritto nel passo immediatamente precedente, il secondo numero più grande veniva a trovarsi nella posizione accanto all’ultimo e così via, fino a che tutti i numeri risultavano riordinati in ordine crescente. Questo processo richiedeva l’esame di tutte le possibili coppie di dati e, pertanto, il numero di operazioni aritmetiche (qui il confronto di due grandezze) era proporzionale a n², se n erano i dati da riordinare. Un’altra misura della complessità di un programma è costituita dal numero di volte che occorre leggere un nastro; nel caso precedente n volte. Un’altra misura ancora può essere la lunghezza del programma richiesto o la dimensione della memoria del computer utilizzata. L’ordinamento che abbiamo appena descritto è detto ordinamento a bolle (bubble sort) per le minuscole bolle di soli due valori che vengono elaborati volta per volta nel computer, è l’algoritmo di riordinamento più semplice tra quelli conosciuti. Inizialmente esso risultava conveniente, essendo la programmazione su un pannello di connessioni (plug-board) difficile e spesso all’origine di numerosi errori; ma ben presto, per quantità significative di dati, sono stati definiti e impiegati criteri e processi di ordinamento più efficienti i quali, a ogni lettura del nastro, sistemano nel loro ordine finale un maggior numero di dati.

Consideriamo un insieme di dati, ognuno dei quali sia etichettato con una chiave costituita da un numero intero di una o due cifre e venga perforato su una scheda. Agli inizi del XX sec. si esaminavano tutte le schede con una macchina di Hollerith, separandole in dieci pacchetti (corrispondenti ai dati aventi chiave da 1 a 10, da 11 a 20 e così via); quindi si classificavano le schede dei singoli pacchetti ordinandole in base alla seconda cifra della chiave; infine un’ultima lettura le riordinava in base alla prima cifra. Agendo in tal modo la complessità di programmazione è uguale a 2 (quanti sono i passi necessari all’ordinamento di schede contenenti dati di chiave inferiore a 100). Altre strategie, più complicate, possono adattarsi a casi più generali, ma si potrebbe dimostrare che esse richiedono un numero di cicli pari alla parte intera di logn, essendo il logaritmo in base 10 e n il numero dei dati da riordinare. Un esempio di algoritmo di complessità logn, più facile da descrivere rispetto al caso della classificazione, è quello che costruisce la trasposta di una grande matrice di numeri, memorizzata su nastro. Una matrice, o vettore (array) bidimensionale di dati, si può indicizzare mediante il numero della colonna e della riga in cui si trova il dato da ricercare. Pertanto, indicato con a_ij il generico elemento (posto all’incrocio fra la i-ma riga e la j-ma colonna) di una matrice A di dati, il vettore A si può memorizzare su nastro magnetico ordinandolo secondo le sue righe:

[1] a₁₁, a₁₂,…, a_1n, a₂₁, a₂₂,…, a_2n, …

La trasposta di A è semplicemente la stessa matrice riscritta (riordinata) per colonne, con il primo indice che varia più rapidamente del secondo. Ci si chiede come sia possibile ottenerla usando i nastri e agendo in modo che sia minima la memorizzazione interna al computer. Un approccio possibile richiede 4 nastri e logn+1 letture. In un primo passo si registrano le righe pari su un nastro e quelle dispari su un altro. In un secondo passo si possono allora registrare su un terzo nastro, nell’ordine, gli elementi

[2] a₁₁, a₂₁, a₁₂, a₂₂, …, a_1n, a_2n, …

e su un quarto gli elementi

[3] a₃₁, a₄₁, a₃₂, a₄₂, …, a_3n, a_4n, …

cosicché due elementi alla volta su ogni nastro risultano in ordine trasposto. Al terzo passo se ne possono ottenere su ogni nastro quattro alla volta in ordine trasposto. Alla fine, dopo logn+1 passi, tutti gli elementi della matrice A risultano riordinati per colonne, essenzialmente senza aver richiesto memorizzazione interna al computer.

Negli anni Cinquanta erano già emerse strutture più complesse delle liste lineari e ottimizzazioni più complicate rispetto alla riduzione del numero di letture di un nastro. Edsger W. Dykstra, per esempio, aveva sviluppato un efficiente algoritmo per individuare il cammino più breve tra due nodi di un grafo, risolvendo vari problemi sorti nell’automazione della progettazione di computer. Un grafo è una struttura matematica che consiste di punti (vertici) e collegamenti tra i vertici (spigoli) e che può essere descritta mediante matrici di adiacenza, che indicano quali vertici sono connessi da spigoli. Queste matrici costituiscono i primi esempi di strutture di dati che consentono di rappresentare in modo efficiente oggetti matematici complessi nella memoria del computer e di ripercorrerli e modificarli durante una ricerca. L’algoritmo menzionato introduceva una tecnica ora nota come breadth-first search. Se tutti gli spigoli di un grafo, per esempio, sono di uguale lunghezza, abbiamo bisogno di individuare il cammino con meno spigoli verso un qualsiasi nodo a partire da una qualche origine. Dapprima si trova il cammino banale verso ogni nodo vicino all’origine; poi il cammino più breve verso ogni nodo vicino ai nodi raggiunti nel passo precedente. Questo processo si ripete finché non si raggiunge la destinazione desiderata. Ogni nodo deve essere analizzato solo una volta e il costo del calcolo dell’analisi è proporzionale al numero di connessioni che partono dal nodo stesso. Se un grafo ha n nodi e una media di k spigoli fuoriuscenti da ogni nodo, il numero totale di istruzioni necessarie per eseguire questo algoritmo è proporzionale a nk.

Per creare strutture e algoritmi così complessi sono stati necessari programmi come gli assemblatori, gli interpreti, i compilatori e i linker, che si sono sviluppati a piccoli passi. Il primo è stato il linker, uno strumento che decide dove (nella memoria del computer) caricare il programma applicativo da eseguire, individua tutti gli altri programmi cui il primo potrebbe trasferire il controllo e memorizza queste informazioni di collegamento in memoria, tra le istruzioni del programma applicativo. Gli assemblatori sono traduttori che mettono in corrispondenza ogni istruzione del programma con una o più istruzioni macchina e usano istruzioni strettamente legate alle caratteristiche hardware dello specifico computer. Supponiamo di voler sommare due numeri (già memorizzati nel computer) e di memorizzare il risultato. Nei computer più semplici (come una calcolatrice tascabile) l’addizione si può eseguire in un registro accumulatore (brevemente, accumulatore) e il codice assembler apparirebbe così:

LDA 2000

[4]     ADD 2001

STA 2002

La prima delle istruzioni [4] è un comando che impone al computer di caricare nell’accumulatore il contenuto della locazione di memoria di indirizzo 2000 (il primo numero, qualunque esso sia); la seconda istruzione gli chiede di sommare al contenuto dell’accumulatore (il primo numero) il contenuto della locazione di memoria 2001 (il secondo numero, qualunque esso sia) e di memorizzare il risultato dell’operazione nel registro stesso (cosicché, eseguita questa istruzione, l’accumulatore non contiene più il primo numero ma la somma dei due numeri); infine, la terza istruisce il computer affinché memorizzi il contenuto dell’accumulatore (la somma dei due numeri, qualunque essa sia) nella locazione di memoria di indirizzo 2002.

Le istruzioni assembler (e le corrispondenti istruzioni macchina) possono essere molto più complesse di quelle illustrate in questo esempio. È allora evidente il vantaggio di disporre di un programma compilatore, che genera una sequenza corretta di istruzioni macchina per un algoritmo espresso in forma di un’equazione o di una formula. In effetti, è molto più facile scrivere C=A+B e lasciare al computer il compito di trattare i dettagli mediante il suo compilatore (che ha la funzione di tradurre l’espressione in linguaggio macchina).

I programmi interprete occupano una posizione intermedia fra gli assemblatori e i compilatori. Gli assemblatori e i compilatori creano una sequenza corretta di istruzioni macchina, all’occorrenza collegate con altre routine; tali istruzioni, una volta esaminate dal linker, vengono eseguite dal computer. Con un interprete la descrizione originale di alto livello, o umanamente leggibile (il codice sorgente, source code), dell’algoritmo viene interpretata ed eseguita immediatamente riga per riga. L’interprete genera via via le istruzioni macchina. Il linguaggio FORTRAN e il suo compilatore furono sviluppati da John W. Backus e introdotti dall’IBM nel 1957 mentre LISP, un linguaggio interprete per la manipolazione di espressioni logiche, fu inventato da John McCarthy nel 1958 ca. (anch’esso con un compilatore), entrambi sopravvivono ancora in forme molto raffinate, a differenza di molti altri elaborati successivamente.

A tutt’oggi è difficile capire come mai ci sia voluto tanto tempo, all’epoca, per riconoscere l’impatto rivoluzionario che il calcolo digitale avrebbe avuto. Vannevar Bush – che diresse da Washington, durante la Seconda guerra mondiale, tutte le attività scientifiche a sostegno dello sforzo bellico – nel 1945 pubblicò un saggio sulla tecnologia, di grande interesse per ampiezza e capacità di previsione ma caratterizzato anche da punti deboli e omissioni. Egli riconobbe che molte tecnologie avrebbero potuto continuare la loro costante accelerazione, che lo sforzo bellico aveva dimostrato possibile, ma non comprese che il calcolo digitale era l’unico a poter essere applicato sostanzialmente a tutti i problemi che egli prendeva in considerazione. Prima della guerra Bush, professore di ingegneria elettronica, aveva costruito alcuni dei primi computer analogici ritenendo che la principale sfida del XX sec. sarebbe stata legata alla necessità di organizzare tutta la conoscenza umana, e di tenersi aggiornati rispetto al suo ritmo accelerato di accumulazione, rendendosi così conto che la memorizzazione di queste informazioni poteva miniaturizzarsi drasticamente. I computer possono aiutarci nell’esaminarle, in particolare memorizzando i nostri percorsi preferiti e gli indirizzi di computer remoti contenenti informazioni di nostro interesse, idee alle quali è stata data forma concreta solo recentemente, negli iperlink e bookmark usati nella navigazione attraverso il world wide web (Internet). Bush predisse che il computer avrebbe potuto riconoscere il linguaggio e trasformarlo in testo scritto ma pensava che la miniaturizzazione dei dati si potesse ottenere sviluppando la tecnologia analogica dei microfilm. Lo strumento che egli immaginava impiegato nell’attenta visione dello scibile sembrava essere più un lettore di microfilm da biblioteca e non pensò mai a reti di dati, che ora rendono possibile la condivisione di informazioni fra computer remoti, oppure alla memorizzazione a lungo termine delle informazioni. Di certo potrebbe sorprendersi molto oggi, nel constatare che il computer viene utilizzato da tutti, non solo dagli scienziati e studiosi.

L’età degli algoritmi (1960-1980): ancora un periodo per specialisti

Gli utenti dei primi computer affrontarono subito separatamente i problemi inerenti alla codifica di programmi applicativi e quelli relativi alla gestione degli apparati tecnologici per la lettura o l’ingresso (input) dei dati necessari alle varie elaborazioni e per la loro registrazione o uscita (output), individuando sia le condizioni di errore sia tutto ciò che attiene ai compiti di gestione del software. Tale gestione venne automatizzata nel software monitor, il progenitore del moderno sistema operativo. I primi monitor consentivano di caricare e di eseguire un programma applicativo alla volta e di disporre dei risultati al termine dell’elaborazione. Le routine di servizio (utilities) che gestivano i registratori a nastro, le macchine da scrivere o le stampanti crebbero velocemente in complessità. Nel 1963 l’IBM sostituì i suoi vari calcolatori scientifici e finanziari con una singola famiglia di computer, i System/360, la performance dei quali era misurabile in un intervallo di valori che andava da 1 a 20 e il cui sistema operativo, OS/360, costituiva il più grande progetto di software mai affrontato a quel tempo. Raggiungere tutti gli obiettivi progettuali richiese parecchi anni dopo la comparsa dei primi computer IBM/360, con i quali si affermò un altro livello di programmazione. Dotate di un insieme comune di istruzioni di calcolo, tutte le macchine (a parte quelle a più alta performance) usavano i microcodici, istruzioni situate nel computer, per implementare realmente le istruzioni eseguite sullo specifico hardware. In questo modo lo stesso programma poteva girare su tutti i computer della famiglia, ma a velocità differenti, che verso la fine degli anni Sessanta si misuravano in un intervallo di valori da 1 a 200.

Il primo sistema multi-utente, in grado di condividere le risorse del computer fra più programmi in esecuzione, fu il CTSS del MIT, sviluppato intorno al 1963. Esso poteva servire contemporaneamente fino a 32 utenti e diede origine all’espressione condivisione temporale (time sharing), consentendo per la prima volta la possibilità di collaborazione tra utenti, facilitata dal computer. Il sistema operativo UNIX, e il suo linguaggio di programmazione C, sviluppati insieme nei Bell labs della Apple computers a partire dal 1969, seguirono un approccio differente per raggiungere l’obiettivo di supportare molti differenti tipi di computer. Il C, che viene ancora largamente usato, offre sia strutture logiche eleganti sia la capacità di controllare caratteristiche hardware del computer come i singoli bit nella memoria e nei registri. UNIX è scritto quasi interamente in C e il codice assembler appare soltanto in alcune parti del kernel, il nucleo del sistema operativo contenente il codice specifico della macchina. UNIX era distribuito agli utenti nel suo codice sorgente in C e gli utenti lo dovevano poi compilare nei loro computer. Mentre il software originale era distribuito sotto licenza, la possibilità di disporre di un codice sorgente come documentazione definitiva stimolò alcuni informatici a sviluppare versioni open source di UNIX e delle sue utilities più popolari, disponibili gratuitamente.

All’inizio degli anni Settanta la più importante applicazione dei computer era costituita dai database aziendali centralizzati, nei quali i dati sulle operazioni delle società erano raccolti in archivi digitali (record). L’aggiornamento di queste informazioni era controllato a livello centrale per garantire tempestività e accuratezza. Le relazioni tra questi archivi e il loro contenuto, che costituisce l’attività della società, consistevano in programmi in grado di produrre rapporti per il management dell’impresa oppure di dare il via ad azioni specifiche, quali la ricostituzione delle scorte in caso di esaurimento di un articolo o l’emissione di fatture. Nei sistemi più vecchi le relazioni tra archivi di dati erano implicite, spesso conseguenti alla gerarchia propria del sistema di organizzazione e gestione dei file nei quali venivano memorizzati i dati; ciò rispecchiava in modo assai rigido gli accordi commerciali concernenti le prime tecnologie di stoccaggio. Studi successivi consentirono di definire tali relazioni in modo indipendente dai dati, come una rete di puntatori. L’approccio moderno dell’architettura dei database, il database relazionale, fu elaborato negli articoli di Edgar F. Codd a partire dal 1970. Codd tratta gli oggetti nei database e le relazioni tra di loro sullo stesso piano, allo scopo di definire il modello dei dati dell’azienda e delle sue operazioni comprensibili all’utente finale, nascondendo i dettagli di implementazione. I prodotti che seguirono questo approccio sono stati largamente accettati, anche se ci vollero quasi tutti gli anni Settanta perché ciò avvenisse.

L’esposizione del database relazionale di Chris J. Date, nel suo autorevole libro An introduction to database systems, giocò un ruolo chiave nella diffusione di queste idee. Esso apparve nel 1974, anno in cui ancora nonesistevano prodotti di database relazionali sul mercato, ebbe sette edizioni e viene tuttora stampato. La progettazione dei database in un successivo sviluppo, la programmazione orientata agli oggetti (un’importante evoluzione della metodologia di sviluppo del software), catturò l’interesse di una larga parte della comunità della computer science.

Un secondo cambiamento radicale iniziò ad affermarsi intorno al 1960. Le prime proposte furono avanzate per la trasmissione di dati digitali attraverso reti telematiche condivise da più utenti, sotto forma di pacchetti (blocchi di bit contenenti, insieme ai dati da inviare, l’informazione sull’indirizzo del computer cui gli stessi dati erano destinati). Nel 1962, John C.R. Licklider propose una rete galattica di computer interconnessi e, per realizzare tale intuizione, fondò una piccola organizzazione presso l’Advanced research projects agency (ARPA) del Dipartimento della difesa degli Stati Uniti. Nel 1965 si testarono le prime connessioni di computer dalla costa del Pacifico alla costa dell’Atlantico. Nel 1970 i computer di una dozzina di università e di centri di ricerca sparsi per gli Stati Uniti parteciparono al primo progetto ARPAnet, in cui l’unico servizio fornito era il collegamento in rete (log in) e l’esecuzione di programmi in remoto (telnet). Nel 1972 si aggiunse all’offerta la posta elettronica (e-mail) e il simbolo @ fu scelto da Ray Tomlinson della Bolt Benarek & Newman per identificare un indirizzo elettronico. Occorre sottolineare che in quel periodo esisteva già una rete di comunicazione globale, ossia la rete telefonica analogica, che funzionava in maniera altamente affidabile e con buona qualità della voce ma non era specificamente adatta per la trasmissione di dati digitali. D’altra parte i proprietari e gli operatori della rete vocale telefonica non erano particolarmente interessati, per ragioni economiche, alla trasmissione di dati. La situazione sarebbe tuttavia cambiata.

Toccò poi alla grafica, intesa come creazione, memorizzazione e trasmissione di immagini sia statiche sia in movimento, trasformarsi dalla forma analogica alla forma digitale. Le tecnologie analogiche di trattamento delle immagini, per esempio la fotografia, il film e il microfilm (il supporto preferito da Bush), erano diffuse. Sin dagli anni Trenta la televisione aveva reso possibile la gestione di immagini elettroniche e nel 1950 venne definito lo standard NTSC per le trasmissioni video a colori. Lo schermo del computer poteva essere trattato in maniera sia analogica sia digitale. L’approccio analogico consentiva di scrivere sullo schermo con una penna luminosa mobile, proprio come si disegna su un pezzo di carta. Il disegno di linee analogico, chiamato grafica vettoriale, costituiva una tecnica largamente diffusa; per esempio, la Boeing la impiegò attorno al 1960 per ottenere disegni generati al computer con i quali vedere come i piloti di taglia media si sarebbero trovati nelle cabine di guida degli apparecchi futuri, dando così origine all’uso della locuzione grafica computerizzata (computer graphics). In alternativa, lo schermo del computer poteva essere trattato come una matrice di punti possibili a risoluzione grafica fissata. Questi punti (pixel) erano definiti da valori numerici interi calcolati automaticamente e memorizzati nel computer. Anche se tutto ciò si rivelò inizialmente piuttosto dispendioso e di non agevole attuazione, ben presto venne reso disponibile l’hardware, veloce ed economico, idoneo alla grafica digitale e durante gli anni Sessanta e Settanta furono messe a punto tecniche per la creazione di immagini altamente realistiche mediante il semplice calcolo dei pixel che le costituivano, cosicché la grafica vettoriale cadde in disuso già alla fine di quel periodo.

La competizione e la performance artistica hanno svolto un ruolo importante nella successiva evoluzione della computer graphics. Nel 1963 la prima competizione di arte per computer portò all’ideazione dello SKETCHPAD, un programma scritto da Ivan Sutherland al MIT, mentre la competizione annuale per cortometraggi animati al computer, il SIGGRAPH, fu per molti anni l’occasione nella quale si sperimentavano tecniche che presto si sarebbero utilizzate nei film e nelle arti commerciali di ogni genere. Nel 1966, Sutherland e Bob Sproull realizzarono uno schermo head-mounted, con tracciamento in tempo reale della posizione e dell’orientazione dell’utente allo scopo di creare un ambiente di realtà virtuale. I primi sistemi grafici utilizzavano la grafica vettoriale, ma le tecniche che impiegavano i pixel dominarono dalla metà degli anni Settanta in poi. I primi progressi consistettero in metodi molto rapidi di interpolazione e ombreggiatura per ottenere superfici curve che sembrassero reali. I successivi metodi a raggio tracciante (ray-tracing) permisero l’illuminazione di un oggetto da parte di più sorgenti di luce. Gli Z-buffers, che calcolavano la profondità dell’immagine, consentivano di rendere visibili (portandoli in primo piano) gli oggetti più vicini all’osservatore, bloccando sullo sfondo dello schermo gli altri oggetti e rendendo in tal modo possibile la rappresentazione in tempo reale di scene complesse. Un’ultima tecnica è la mappa di struttura (texture mapping), in cui una superficie simulata è avvolta intorno alla superficie dell’oggetto modellizzato.

Durante gli anni Sessanta l’attenzione iniziò seriamente a rivolgersi all’interfaccia con il computer, ossia alle tecniche di interazione fra utente e computer. Nel suo periodo di maggior successo, dal 1963 al 1968, l’Augmentation research center di Doug Engelbart, un grande gruppo dello Stanford Research Institute, inventò il mouse ed esplorò le prime forme della maggior parte di quelli che oggi sono gli elementi delle interfacce grafiche degli utenti (graphics user interface). Engelbart condivideva con Licklider e Robert Taylor, i due promotori del progetto ARPAnet, la visione del computer come mezzo per accrescere le capacità umane di compiere lavoro scientifico mediante la collaborazione con colleghi eventualmente distanti. Come si conviene alle innovazioni nel campo della collaborazione, un’area a quell’epoca poco apprezzata, l’importanza del lavoro di Engelbart e dei suoi ricercatori non fu avvertita attraverso i suoi articoli, brevetti o prodotti bensì per mezzo delle dimostrazioni pubbliche e con la migrazione delle persone del suo gruppo nei laboratori della Xerox PARC, della Apple computers e di altre importanti aziende. Nel suo intervento pubblico più famoso, alla Fall joint computer conference del 1968 a San Francisco, Engelbart presentò, tra l’altro, la videoconferenza, il mouse, la collaborazione su uno schermo condiviso, gli iper-link, l’elaborazione di testi e la ricerca in tempo reale in un database per parole chiave.

In quel periodo la teoria degli algoritmi fece grandi progressi, contribuendo in modo efficace alla risoluzione di molti problemi. Alcuni testi scritti all’epoca rappresentano ancora oggi dei caposaldi come, per esempio, l’esauriente The art of computer programming di Donald E. Knuth, un’opera in tre volumi pubblicata per la prima volta a metà degli anni Sessanta che continua tuttora a essere aggiornata. Essa costituisce il test di base più completo e fornisce un quadro storico e matematico della teoria degli algoritmi. Si sviluppò un’ampia letteratura sulla complessità dei problemi e una delle prime questioni affrontate fu la complessità dell’aritmetica stessa. Dati due numeri u e v, ognuno con 2n bit di informazione, ci si aspetterebbe che il loro prodotto richieda 4n² operazioni di moltiplicazione tra bit; decomponendoli però nei rispettivi bit di ordine alto e di ordine basso:

[5] u=2ⁿu₁+u₀, v=2ⁿv₁+v₀

si trova che il prodotto uv può essere scritto come segue

[6] uv=(2²ⁿ+2ⁿ)u₁v₁−2ⁿ(u₁−u₀)(v₁−v₀)+(2ⁿ+1)u₀v₀

La [6] consente di calcolare il prodotto di due numeri ognuno con 2n bit mediante tre moltiplicazioni, tutte fra due numeri a n bit, seguite da alcune traslazioni di bit (shift) e infine da addizioni. Questo risultato non solo fornisce un’indicazione precisa del numero di bit che può essere moltiplicato nell’hardware a disposizione ma è anche alla base di una procedura ricorsiva. In effetti, per calcolare il prodotto di due numeri è possibile scomporli entrambi in due parti (contenenti, rispettivamente, i bit di ordine alto e i bit di ordine basso) e poi applicare la stessa procedura alle parti, continuando così finché non si sia in grado di ottenere i prodotti parziali desumendoli da una tabella (o in qualche altro modo). Se si può trascurare il costo degli shift e delle addizioni, come avveniva nei primi computer (nei quali la moltiplicazione era molto lenta), il tempo T_2n richiesto per moltiplicare due numeri a 2n bit diviene, approssimativamente, 3T_n; si trova che T_n è proporzionale a n^log3. Questo tempo è inferiore al tempo n², inizialmente previsto, e ciò è significativo almeno per numeri abbastanza grandi, quando il tempo di traslazione e di addizione che si è trascurato si può, in effetti, ignorare.

Questo tipo di approccio ricorsivo, sia algoritmico che analitico, caratterizza i risultati della computer science degli anni Cinquanta e Sessanta. Un risultato di questo tipo, ancora più sorprendente, è che il prodotto fra matrici si può ottenere con un risparmio sul numero di moltiplicazioni grazie a una procedura ricorsiva di decomposizione nel prodotto fra matrici più piccole. Volker Strassen mostrò per primo che, se il prodotto di due matrici quadrate di ordine 2n è fattorizzabile nel prodotto di matrici quadrate di ordine n, un ingegnoso metodo di combinazione delle matrici più piccole consente di ottenere il risultato finale con appena sette moltiplicazioni matriciali, invece delle otto previste. Dunque, il tempo necessario per moltiplicare due matrici quadrate di ordine n può essere reso proporzionale a n^log7, invece che a n³. Procedure molto più complesse vennero successivamente definite per ridurre il limite asintotico a n²³⁷⁶. L’effettivo costo limite può ancora essere ridotto, se si riescono a definire ulteriori schemi di ottimizzazione. Tuttavia l’effettiva utilizzazione della procedura appena descritta è così dispendiosa da rendere i metodi ricorsivi di moltiplicazione matriciale raramente usati nella pratica che pertanto rimangono curiosità teoriche.

I risultati di questa fase di sperimentazione degli algoritmi più largamente utilizzati sono le strutture di dati e i metodi efficienti per la ricerca e l’ordinamento di dati e l’esecuzione di molti tipi di ottimizzazioni di sistemi descritti come grafi o reti. Essi divennero tecniche fondamentali non appena i computer ebbero sufficiente memoria da consentire l’esecuzione di tutti i calcoli al loro interno. L’analisi, però, assume ora un carattere probabilistico, con diversi aspetti nuovi al suo interno. Si consideri per esempio un vettore (array) di molti numeri, interamente nella memoria del computer. Una tecnica assai efficiente per ottenerne l’ordinamento ascendente si basa su un algoritmo ricorsivo noto come quicksort. La sezione critica del quicksort è una routine software che ripartisce opportunamente un array di numeri. Scelto un membro del vettore come elemento cardine (pivot), si ripartiscono gli altri numeri in due gruppi di memoria contigui in modo che il gruppo inferiore contenga i numeri minori o uguali al pivot e il gruppo superiore quelli maggiori; il pivot viene quindi memorizzato fra i due gruppi. Infine, si applica la routine di ripartizione prima al gruppo inferiore e poi al gruppo superiore, continuando ricorsivamente finché la ripartizione fornisce un singolo numero o un gruppo di numeri tutti uguali. Con una buona programmazione questo algoritmo può assai velocemente ordinare grandi vettori, pur essendo sensibile alla successione iniziale dei numeri e alla scelta del pivot.

Supponiamo di essere assai sfortunati nella scelta dei pivot e che ogni ripartizione di n numeri produca un vettore inferiore di n−1 elementi, un pivot e un vettore superiore vuoto. In questo caso il procedimento non è più efficiente del bubble sort, richiedendo n² confronti fra coppie di numeri. In realtà, si tratta di un’eventualità abbastanza frequente che potrebbe presentarsi quando il vettore è già quasi ordinato, ossia ha solo pochi numeri in posizione errata. D’altro canto, se ogni ripartizione divide gli n numeri in due gruppi uguali di circa n/2 elementi, il procedimento termina dopo logn passi, ognuno dei quali comporta n confronti. In conclusione, il costo dell’ordinamento può essere stimato nella migliore delle ipotesi in nlogn confronti e nel caso peggiore in n² confronti.

È naturale domandarsi quale sia il costo medio di un particolare algoritmo di ordinamento su differenti array di dati. Per rispondere a questa domanda è necessaria una misura di probabilità sugli ordinamenti iniziali degli array. Se tali ordinamenti sono equiprobabili, la risposta è che quasi tutti gli ordinamenti finali vengono ottenuti con il quicksort con circa nlogn confronti, cosicché il costo medio è effettivamente proporzionale a nlogn. L’algoritmo è tuttavia migliorabile in due modi. Si può impiegare del tempo extra nella scelta di buoni elementi pivot oppure, con un processo di randomizzazione, si può ricorrere a ordinamenti iniziali casuali per garantire che ogni ordinamento finale si possa ottenere in nlogn passi. La seconda strategia consiste semplicemente nello scegliere a caso l’elemento pivot prima di iniziare i passi di ripartizione. Questo modo di operare produce ripartizioni quasi bilanciate anche a partire da dati inizialmente ordinati. La caratteristica che i costi computazionali del quicksort nel caso peggiore e nel caso medio differiscano molto se applicati a vettori numerici assai grandi è molto comune. L’uso di un elemento pivot scelto a caso per garantire, con probabilità alta, un impiego efficiente dell’algoritmo è anche ampiamente applicabile, benché in casi speciali non consenta di cogliere le opportunità di ulteriore riduzione del tempo di esecuzione.

Dopo la messa a punto di algoritmi applicabili alla maggior parte dei problemi di ordinamento del tipo di quelli precedentemente descritti, l’attenzione fu rivolta ai cosiddetti problemi intrattabili, la cui classificazione è una questione sottile, nella quale le definizioni matematiche non sempre contano nella pratica. Sono ovviamente intrattabili i problemi potenzialmente irrisolvibili, come il problema della fermata, ma ve ne sono anche molti altri per i quali a causa delle situazioni iniziali peggiori il tempo di calcolo cresce, al crescere di n, come exp(n/n₀) con n₀ costante opportuna. Questi problemi appaiono a loro volta intrattabili in quanto, anche se risolubili su un computer sufficientemente potente quando la dimensione n è abbastanza piccola, l’aggiunta di un numero di elementi multiplo di n₀ potrebbe incrementare il costo del calcolo di un fattore pari almeno a dieci, rendendolo di fatto irrealizzabile.

Tuttavia negli esempi più noti, quali i cosiddetti problemi NP-completi, la dimostrazione della complessità esponenziale ancora sfugge e, se si escludono alcuni casi, buone approssimazioni sono spesso in grado di raggiungere soluzioni accettabili (in termini di tempo di calcolo) o addirittura ottimali. Se per un siffatto problema decisionale ci si propone di verificare una soluzione proposta, lo si può fare in un tempo che è funzione polinomiale (e non esponenziale) di n. Dunque un ipotetico computer ad architettura altamente parallela, in cui ogni unità parallela verifichi una possibile dimostrazione della risposta, può risolvere il problema decisionale in un tempo polinomiale. Sfortunatamente, il numero di unità parallele richieste per la verifica della risposta cresce almeno esponenzialmente con n.

Un esempio tipico è il problema del commesso viaggiatore, in cui un commesso nel tempo più breve possibile deve visitare n città, per poi ritornare al punto di partenza. Per risolvere questo problema di ottimizzazione si cerca il cammino più breve attraverso n punti le cui distanze reciproche siano note e che riconduca, alla fine, al primo punto. Si è così ricondotti a un problema decisionale (fissato un numero L, vi è un cammino la cui lunghezza sia minore di L?) che è NP-completo. Per risolverlo si potrebbero elencare tutte le sequenze possibili delle città, considerare le loro distanze reciproche e fermarsi non appena si trova un cammino di lunghezza inferiore a L. Ci sono, però, (n−1)(n−2)(n−3)…=(n−1)! cammini possibili, un numero che cresce più velocemente di exp(n). Benché sia possibile eliminare facilmente i cammini più lunghi di L, per quanto si sa non esiste una procedura che garantisca di trovare un cammino di lunghezza inferiore a L o che dimostri che esso possa essere costruito senza prendere in considerazione un numero di cammini grande come exp(n). Stephen A. Cook definì per primo questa nozione di classe di problemi di così difficile soluzione; Richard M. Karp mostrò poi che un metodo di riduzione standard poteva ricondurre molti importanti problemi alla classe dei problemi NP-completi, una lista che comprende ora migliaia di casi.

Contemporaneamente alla rapida crescita della lista dei problemi NP-completi, ingegneri e matematici cominciarono a risolverne alcuni, di dimensioni piuttosto elevate, riguardanti gli orari delle compagnie aeree, la logistica d’inventario e la progettazione computerizzata. Risolvere significava per loro ottenere una soluzione realizzabile che, anche se non ottimale, fosse sufficientemente buona da soddisfare i requisiti di qualità del prodotto e le date di consegna. Si svilupparono programmi euristici, manifestamente migliori dei metodi manuali, i cui tempi di esecuzione crescevano come qualche potenza di n ma non fornivano alcuna garanzia di soluzione ottimale. Inoltre si scoprì che algoritmi esatti, che si fermano solo quando individuano la soluzione ottimale, spesso potevano fornire risultati accettabili anche prima di fermarsi o comunque in un tempo ragionevolmente breve. Identificare le caratteristiche del problema che rendevano possibile la soluzione euristica era, ed è ancora, un problema irrisolto. Divenne chiaro, però, quanto fosse grande il divario tra il costo delle soluzioni nei casi peggiori e il costo tipico. Quando si ha un insieme statistico di casi costituenti un problema NP-completo, con caratteristiche generali simili, spesso si trova che quasi tutti i costi delle soluzioni osservate sono funzioni polinomiali in n.

Alla fine degli anni Settanta diversi ricercatori riconobbero un’analogia tra una classe di problemi di ottimizzazione e i metodi di simulazione adottati nello studio delle proprietà dei sistemi fisici disordinati o caotici. Miglioramenti iterativi degli algoritmi euristici vengono impiegati per individuare configurazioni ragionevoli di sistemi fisici con molti gradi di libertà, o parametri. Si prende una configurazione realizzabile ma non ottimale, si sceglie uno dei parametri che possono essere variati e poi si cerca per esso un nuovo valore che migliori il costo o la qualità totale del sistema, misurati da una data funzione costo. Quando non si ottengono più miglioramenti la ricerca si ferma a quella che potrebbe essere la configurazione ottimale ma che, il più delle volte, corrisponde a una sorta di minimo locale della funzione costo. L’analogia è semplice: i gradi di libertà sono gli atomi del sistema fisico; i vincoli e la funzione costo corrispondono all’energia del sistema. La ricerca eseguita con miglioramenti iterativi è molto simile alla modellizzazione dell’evoluzione dei sistemi fisici, ma con un’importante differenza: i sistemi fisici possiedono una temperatura, che stabilisce la scala delle variazioni di energia sperimentate da un atomo durante l’evoluzione del sistema. Ad alte temperature sono permessi moti casuali mentre a temperature più basse la ricombinazione atomica conduce in maniera naturale all’organizzazione del sistema e, se ci si avvicina abbastanza lentamente al limite di temperatura zero, il sistema raggiunge lo stato di energia minima. Questa analogia con la meccanica statistica ha anche consentito, in alcuni casi, predizioni accurate di risultati attesi per un vasto insieme di problemi, come per esempio quello del commesso viaggiatore.

Dal 1980 a oggi: vincono gli utenti

La fine dell’era del computer come settore specialistico e la sua attuale posizione centrale nell’economia mondiale, essenzialmente in quanto prodotto di consumo, sono una conseguenza della legge di Moore, cioè dell’osservazione empirica che i componenti elettronici riusciti, prodotti in massa ogni anno, aumentano in capacità di un fattore costante. Il tasso di crescita della potenza di un singolo chip è esponenziale: infatti, il primo chip di memoria, con 1024 bit, fu introdotto nel 1971, i chip con 1MB (megabyte) circa dieci anni dopo e quelli da 1GB (gigabyte) sono adesso di uso comune. Una simile crescita esponenziale, benché con tassi differenti, si osserva nella logica del computer, nelle tecnologie di memorizzazione, come i dischi magnetici, e perfino nelle batterie.

Le batterie sono fondamentali per i computer portatili e per i telefoni cellulari e negli ultimi cinquant’anni la loro capacità è aumentata di circa un fattore due ogni dieci anni. La loro legge di Moore non è così favorevole perché le batterie non beneficiano direttamente delle tecnologie che creano circuiti ogni anno più piccoli mentre i piccoli miglioramenti della chimica devono essere trasformati in procedimenti di lavorazione sicuri e affidabili per far avanzare la produzione industriale; il riscontro economico legato al successo di vendita di batterie dalla durata sempre più lunga ha comunque imposto un tasso di miglioramento di lungo periodo.

Lo sviluppo chiave del computer in quanto prodotto di mercato fu determinato dalla comparsa di microcomputer a singolo chip, a cominciare da quelli come l’Intel 4004 e l’Intel 8080, rispettivamente nel 1971 e nel 1982. Essi erano limitati nelle funzioni, eseguendo operazioni aritmetiche su soli 4 o 8 bit alla volta, e pensati per costituire elementi essenziali di calcolatori e terminali. Con l’Intel 8080 si rendeva disponibile un microprocessore con capacità vicina a quelle di un minicomputer, che venne rapidamente incorporato in semplici computer per appassionati da compagnie quali MITS (l’Altair), Cromenco e North star (ma nessuna di esse sopravvisse a lungo dopo il 1980). Le prime macchine offrivano per la programmazione soltanto versioni del linguaggio BASIC e del linguaggio assembler e un’unità a nastro analogica quale supporto di memorizzazione permanente di dati e programmi.

L’Apple II, che apparve nel 1977, basato sul microprocessore a 8 bit Mostek 6502, offriva un floppy disk come supporto di memorizzazione permanente, con più efficiente capacità di accesso ai dati. Solo nel 1979 però, con l’introduzione del programma Visicalc, fu chiaro che un computer così semplice poteva essere utile anche a clienti che non avevano alcun interesse per la tecnologia. In Visicalc, sviluppato da Dan Bricklin e Bob Frankston, l’utente poteva inserire numeri o espressioni in un modulo memorizzato come quadro bidimensionale che era già familiare ai contabili e agli studenti di economia e di facile apprendimento per chiunque avesse bisogno di gestire conti o inventari. Modificando una quantità nel modulo si aggiornavano automaticamente i risultati, cosicché diverse ipotesi potevano essere immediatamente esplorate. Programmare inserendo formule semplici direttamente in una tabella di dati si mostrò inaspettatamente facile da capire e da usare per i non programmatori. Si noti che Visicalc fu preceduto da un lavoro sui linguaggi di input diretto, come il QBE (Query by example), che nei cinque anni precedenti aveva permesso al singolo utente di compilare un modulo e di inviarlo a un computer condiviso con altri utenti, simulando automaticamente un’ipotetica transazione finanziaria. Tuttavia, il QBE che con le sue estensioni operava nei grandi elaboratori (mainframe) non agevolava l’utente programmatore e pertanto non riuscì mai ad avere ampia diffusione.

L’immediatezza dell’ambiente del personal computer fece la differenza. Apple II e Visicalc contribuirono a valorizzare le grandi capacità di questa classe di strumenti e il punto di vista del singolo utente. In 6 anni, i computer basati su microprocessore si erano sviluppati quasi quanto i mainframe e i minicomputer nei 35 anni trascorsi dal 1945. Quando apparve, nel 1981, il personal computer IBM (il PC) non era rivoluzionario nell’hard-ware ma, poiché venne immesso sul mercato al momento giusto, ebbe ampia diffusione. Esso era datato di un sistema operativo semplice di tipo monitor (il DOS della Microsoft), disponeva fin dall’inizio di dischi rigidi ed era sufficientemente aperto da permettere ad altri costruttori di clonarlo e di produrne copie compatibili. Il PC aggiunse al linguaggio del computer un contributo, che è famoso quasi quanto il simbolo @ della posta elettronica su Internet: si tratta della combinazione di tasti Ctrl-Alt-Del, che provocava il riavvio automatico della macchina se premuti contemporaneamente; essa fu introdotta da David Bradley quale combinazione che fosse impossibile produrre accidentalmente.

Durante gli anni Ottanta furono sviluppate sui sistemi monoutente interfacce grafiche per l’utente dotate di non poche funzionalità, con il mouse come mezzo immediato per la scelta di azioni e oggetti sullo schermo; divennero di uso comune varie estensioni di scelta, come il trascinamento di oggetti sullo schermo e il loro rilascio all’interno della finestra di un’applicazione in esecuzione (drag and drop). Queste interfacce grafiche, inizialmente realizzate come prodotti commerciali da Xerox PARC, furono largamente disponibili sui prodotti Apple e sui sistemi UNIX fino dagli anni Novanta e con il tempo divennero uno standard per tutti i sistemi monoutente; fra questi, alla metà del decennio, i PC erano i più diffusi dominando il mercato grazie al loro basso costo e all’ampia gamma di applicazioni.

L’avvento del browser, attraverso il quale si ottiene l’accesso a Internet, ha eliminato completamente la necessità per molti utenti di occuparsi di alcune caratteristiche del computer o del sistema operativo sottostante.

Il primo browser, il Mosaic dell’NCSA (National center for supercomputing applications, presso l’Università dell’Illinois), e i suoi protocolli di rete associati apparvero nella comunità scientifica internazionale nei primi anni Novanta, un periodo in cui coesistevano molteplici tecnologie telematiche per l’accesso a Internet. Dopo il 1995 apparvero i browser commerciali, Netscape e Internet Explorer, supportati da motori di ricerca (quali quelli di Yahoo, AltaVista e successivamente Google) basati su raccolte automatiche estese di contenuti della rete, memorizzate in grandi database relazionali e costituenti di fatto un approccio standard per la ricerca e la disponibilità dell’informazione.

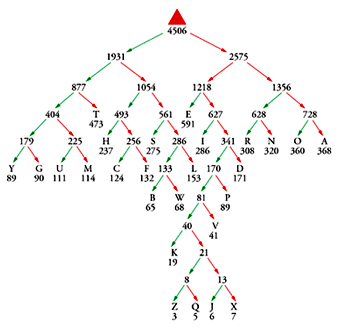
Uno sviluppo importante degli anni Novanta che ha reso possibile la memorizzazione e la diffusione attraverso Internet di dati audio e video è la creazione di famiglie di codici di compressione standard per immagini fisse o in movimento, ad alta o bassa risoluzione, e per le relative colonne sonore e descrizioni vocali. Questo settore ha anch’esso le sue radici negli anni Quaranta, precisamente nella dimostrazione di Claude E. Shannon del 1948 che la variabilità di un insieme di dati impone limiti alla velocità di trasmissione attraverso un canale e alla possibilità di compressione per mezzo di codici. Una strategia naturale per codificare un messaggio in modo da renderlo il più breve possibile consiste nell’adottare i simboli di codice più corti per i caratteri più frequentemente usati, metodo intuitivamente ovvio anche prima che la teoria dell’informazione di Shannon ponesse una rigorosa base teorica. Il codice Morse per il telegrafo (inventato negli anni Trenta dell’Ottocento) per esempio, usa il punto per la E, la linea per la T, il punto-punto per la I, il punto-linea per la A e la linea-punto per la N essendo queste le lettere più comuni, mentre codifica una lettera rara come la Q con una sequenza più lunga: linea-linea-punto-linea. Il codice Huffman, definito nel 1952, ordina tutti i simboli in base alla loro frequenza nei possibili messaggi e costruisce un albero binario le cui foglie costituiscono l’alfabeto di simboli da codificare (Tavola I). Partendo dalla radice dell’albero, la sequenza di deviazioni a destra e a sinistra che conduce a un simbolo del messaggio rappresenta il codice per quel simbolo. La possibilità di compressione del codice così definito si avvicina al limite inferiore indicato da Shannon quando si codificano messaggi sufficientemente lunghi che siano coerenti con la statistica prevista. Dopo il 1952 furono sviluppati codici adattabili che costruiscono le regole di codifica alla prima lettura dei dati e successivamente trasmettono o memorizzano il libro di codice (le chiavi del codice) insieme ai dati da codificare. Il più potente di questi approcci fu introdotto nel 1977 da Jakob Ziv e Abraham Lempel ed è sfruttato nei programmi di compressione più popolari.

Ovviamente il tipo di dati che più beneficia della possibilità di compressione attraverso un’opportuna codifica è il testo. Nella codifica ASCII (American standard code for information interchange) ogni carattere alfanumerico occupa un byte (8 bit). La semplice registrazione ASCII di singoli caratteri, senza la definizione di codici per gruppi di caratteri usualmente ricorrenti, riduce un documento di testo di circa un fattore due senza alcuna perdita di informazione; la codifica Lempel-Ziv riduce un documento delle dimensioni di questo articolo di circa un fattore quattro. Altri codici, i codici correttori d’errore (error correcting codes), possono rendere un documento più lungo se il loro scopo è di aggiungere ridondanza in modo da garantirne la trasmissione attraverso un canale disturbato senza perdita di informazione. È il caso, per esempio, del canale collegato a un apparato tecnologico di controllo della memorizzazione che, con una testina magnetica ad alta sensibilità, legge i bit da un hard disk, li identifica, li codifica nel formato ASCII o binario e li trasmette ad alta velocità all’unità centrale del computer. Infine, va osservato come non sia necessario che i sistemi di codifica preservino tutte le informazioni che costituiscono dati, suoni e immagini, se lo scopo è trasmettere le sole informazioni che alla ricezione siano pronte per essere ascoltate o viste. Tali codici con perdite, orientati alla percezione immediata, sono molto usati nella telefonia e nell’elaborazione e trasmissione di immagini digitali fisse o in movimento; come tali, essi rispondono a regole standard che sono essenziali per una buona riuscita dello scambio di informazioni. In effetti, non basta disporre di uno strumento di codifica efficiente di una conversazione per ottenere che la stessa avvenga a una frequenza ottimale, poiché se nessun altro oltre al mittente adotta un determinato codice essa non può essere ascoltata. Di conseguenza molti sono gli sforzi compiuti da gruppi che rappresentano le industrie operanti nel settore delle telecomunicazioni e dal mondo accademico per valutare i pregi e i difetti dei diversi sistemi di codifica di dati, suoni e immagini; si è ormai creata una consistente lista di pubblicazioni riguardanti i diversi possibili approcci.

L’International telecommunications union (ITU-T, un tempo nota come CCITT, il suo acronimo francese) è l’ente che ha stabilito gli standard per i modem (gli strumenti che trasmettono dati digitali su linee telefoniche analogiche), per la trasmissione di immagini facsimile o halftone (G3 e G4 negli anni Ottanta, poi JBIG negli anni Novanta), per le immagini fisse (JPEG, Joint photographic experts group) e per i filmati (i vari livelli MPEG, Motion picture experts group). JPEG e MPEG hanno operato con continuità sin dalla fine degli anni Ottanta (JPEG) e dagli inizi degli anni Novanta (MPEG), autorizzando la commercializzazione graduale degli standard definiti, con la sponsorizzazione dell’ITU-T e dell’ISO (International standard organization).

I sistemi JPEG e MPEG si basano su standard messi a punto per codificare un singolo fotogramma e per trarre vantaggio dalle correlazioni temporali nell’ambito di una serie di fotogrammi di un filmato. Un pixel, catturato a colori da macchine fotografiche tecnologicamente avanzate, contiene 8 bit di informazione per ognuno dei suoi tre canali, il rosso, il verde e il blu (codifica RGB). L’occhio umano è più sensibile alle variazioni dell’intensità di luce totale che alle variazioni del singolo colore, cosicché il primo passo verso un sistema di codifica legato alla percezione consiste nel sostituire i codici RGB associati ai singoli pixel con una variabile che ne rappresenti la luminosità e altre due che rappresentino i colori. Il secondo passo consiste nel raggruppare i dati dei pixel in piccoli quadranti (generalmente 8×8 pixel) e di considerare la loro trasformata di Fourier, in particolare l’efficiente trasformata del coseno discreto. I bit che rappresentano le frequenze spaziali più alte possono essere ignorati, visto che esse non sono percepite dall’occhio umano. In questo modo i dati di un’immagine possono essere ridotti di un fattore compreso tra 10 e 20 prima di avvertire una qualsiasi diminuzione della sua qualità. Ciascuno degli standard MPEG si è indirizzato su un’applicazione specifica. MPEG-1 si usa per predisporre filmati nel formato dei compact disk, che offre 650 MB di spazio. MPEG-2 veniva usato inizialmente per le trasmissioni televisive digitali su satellite; pertanto il suo principale obiettivo è di massimizzare la qualità dell’immagine entro una banda di trasmissione di 1,5 MB al secondo. MPEG-4, di cui gli elementi più semplici iniziano a essere impiegati nel 2002-2003, punta a supportare frequenze di trasmissione molto più basse, in modo da poter scaricare da Internet e vedere un filmato con un singolo accesso alla rete.

Nel MPEG-1 alcune immagini sono ricostruite tenendo conto della differenza tra immagine e fotogramma precedente. Nel MPEG-2 è utilizzata anche l’interpolazione bilineare, con la quale viene codificata e memorizzata la differenza tra un’immagine e la media fra le immagini precedente e successiva. I tre tipi di codifica delle immagini, I per la struttura di un’immagine, P per quella ricostruita (predicted) e B per la bilineare, fanno parte di uno schema ripetitivo denominato GOP (Group of pictures). Il popolare sistema di codifica DVD, che sta soppiantando le videocassette nella visione domestica dei filmati, per esempio, impiega il sistema MPEG-2 con un GOP di 12 fotogrammi, nella sequenza IBBPBBPBBPBBI…. Per una decodifica efficiente, i fotogrammi vengono trasmessi in disordine e successivamente (alla ricezione) riordinati nel decodificatore prima del riassemblaggio. Altri espedienti usati nel MPEG-2 includono l’identificazione in un fotogramma dei blocchi che cambiano posizione rispetto al fotogramma precedente; questo aiuta moltissimo la codifica di oggetti che si muovono di fronte a uno sfondo statico. Ogni generazione di codifica video (MPEG-1, -2 e -4) offre un miglioramento di almeno un fattore due nella densità della codifica.

Un altro tema riguardante lo studio della complessità è emerso negli anni Novanta, dopo il fiorire della complessità algoritmica, anche se le sue radici risalgono ai primi usi del computer per l’interpretazione dei codici nemici durante la Seconda guerra mondiale. Il lavoro svolto in segreto nei laboratori della cittadina di Bletchley Park portò, nel 1943, al Colossus, il primo grande computer funzionante e programmabile, usato per violare i codici speciali adottati nelle comunicazioni tra Adolf Hitler e i suoi generali. Il governo britannico continuò a lungo, dopo la fine della guerra, le ricerche sulla crittografia, la matematica e gli algoritmi di code-breaking e di comunicazione crittografata ma tenne segreti tutti gli sforzi fatti. Di conseguenza, molti dei risultati che hanno dato forma all’odierna struttura del computer sono stati sviluppati ex novo durante gli anni Settanta da altri informatici e brevettati e commercializzati con successo nel decennio successivo. L’importanza dei contributi britannici è stata riconosciuta soltanto quando gli stessi sono stati resi noti negli anni Novanta.

Il primo strumento elettronico largamente usato, il DES, era basato sul codificatore di Horst Feistel, del 1970. Esso utilizzava originariamente una chiave di codifica a 64 bit, poi ridotta a 56; nel 1974 fu accettato dal governo americano come codice standard, divenendo lo schema di crittografia per uso commerciale più diffuso nel mondo, nonché modello per il trasferimento elettronico di fondi. Per le operazioni di codifica e decodifica viene usata la stessa chiave, che pertanto deve rimanere segreta. Il problema di come fornire la chiave al destinatario di una comunicazione è particolarmente critico per la sicurezza diplomatica e militare, dove sono necessarie chiavi diverse per ogni collegamento, da cambiare con frequenza quotidiana. L’esigenza di uno scambio sicuro di chiavi elettroniche spinse all’invenzione della crittografia a chiave pubblica, dapprima (nel 1969) definita nei suoi concetti fondamentali da James Ellis, il cui lavoro rimase segreto fino al 1997, e poi elaborata indipendentemente e pubblicata da Whitfield Diffie e Martin E. Hellmann nel 1975.

Il trucco sta nel trasferire informazioni riservate da un mittente a un destinatario senza mai inviare dati non crittografati e nel fatto che il destinatario deve partecipare alla cifratura. In tal modo viene condivisa la chiave pubblica, che non ha alcun valore per chi volesse eventualmente intercettare le informazioni, ma il destinatario terrà segreta a tutti, incluso il mittente, la propria chiave privata. Supponiamo che io voglia ricevere una chiave per un codificatore ad alta frequenza, come il DES, da voi, il mittente. Dispongo di due metodi per crittografare, M1 e M3, e voi avete un altro metodo, M2. Questi metodi sono noti a me, a voi e a tutti coloro che potrebbero voler intercettare la nostra conversazione. Io prendo una chiave privata, k (un numero grande che conosco soltanto io), e la crittografo in x usando M1; poi ve la comunico come la mia chiave pubblica. Voi usate x come chiave in M2 (in questo caso una chiave DES) per crittografare il vostro messaggio, m, e me lo inviate nel codice risultante, c. Io uso allora la mia chiave, k, con il metodo M3 per decriptare il messaggio in codice, c, e scoprire m. M1, M2 e M3 devono avere particolari proprietà a senso unico. Se eseguendo M1 in ordine inverso (cioè a partire da x) trovare la chiave k costituisce un problema insolubile in quanto richiede un tempo di calcolo dell’ordine di migliaia di anni, allora si può dire che si dispone di un sistema di crittografia sicuro; analogamente per l’esecuzione in ordine inverso di M2. L’unico problema irrisolto nella proposta originaria di Ellis era la messa a punto di metodi M1, M2 e M3 efficienti. Il suo collega Clifford Cocks individuò nel 1973 alcuni metodi praticabili, anticipando l’algoritmo pubblicato nel 1978 da Ronald L. Rivest, Adi Shamir e Leonard Adleman.

Le funzioni di M1, M2 e M3 devono essere di facile comprensione ma difficili da invertire. La maggior parte dei codici tradizionali si basa su funzioni come la traslazione o la sostituzione all’interno di un alfabeto, che sono facilmente invertibili e perciò, sia pure con grande sforzo, messaggi e chiavi possono essere dedotti. Le tecniche matematiche che portano a funzioni a senso unico sufficientemente robuste, come devono essere M1, M2 e M3, provengono dalla teoria dei numeri primi e dall’aritmetica modulare. Un intero è primo se è divisibile soltanto per sé stesso e per l’unità ed è invece composto qualora lo si possa ottenere moltiplicando fra loro due oppure più interi primi. Pertanto 2, 3, 5, 7, 11 e 13 sono i più piccoli interi primi (0 e 1 non sono inclusi nella lista non essendo fattori validi nella costruzione di interi composti). L’aritmetica modulare è l’aritmetica ristretta all’intervallo di valori fra 0 e un dato numero, n, detto modulo. Quindi, se n è 5, allora 3+3 mod n è uguale a 1, il resto della divisione di 6 per 5.

Il metodo M1 di Cocks consiste semplicemente nel moltiplicare tra loro due numeri primi molto grandi, p e q, e nell’inviare il loro prodotto, n=pq, cioè un numero composto ancora più grande, come chiave pubblica per crittografia. La tecnologia di cifratura del messaggio impiegherà il modulo aritmetico n. M1 è una buona funzione a senso unico, perché non si conosce, al momento, alcun modo in cui un avversario, dato n, possa ritrovare facilmente i fattori p e q se entrambi sono numeri grandi. Nella proposta di Cocks, M2 cifra il messaggio m nel codice c mediante la relazione

[7] M2: c ≡ mⁿ (mod n).

Per decifrare c occorre trovare altri due numeri (che non devono necessariamente essere primi e non sono difficili da costruire), p′ e q′, tali che

[8] pp′ ≡ 1 (mod n), qq′ ≡ 1 (mod n).

Allora entrambe queste relazioni:

[9] M3: m ≡ c^p′ (mod q), m ≡ c^q′ (mod p)

sono in grado di decifrare il messaggio originale m. Nella [7], per elevare m alla potenza n lo si eleva al quadrato ripetutamente (mod n), cosicché il costo di elaborazione risulta proporzionale a logn.

L’algoritmo RSA in uso oggi differisce dal DES appena descritto in alcuni dettagli ma si basa sulle stesse relazioni. Nel cifrario RSA e nel contesto di chiave pubblica il mittente invia un secondo numero, e, insieme a n (o lo mette in una cartella pubblica); e si determina come elemento di una coppia di numeri (d, e) tali che

[10] de ≡ 1 (mod (p−1)(q−1)).

Ora i metodi M2 e M3 divengono

[11] M2′: c ≡ m^e (mod n)

[12] M3′: m ≡ c^d (mod n).

Il primo metodo di Cocks, M2, è un caso particolare di RSA, in cui e=n.

Benché la motivazione originale per la crittografia a chiave pubblica fosse la distribuzione delle chiavi, essa soddisfa molte altre esigenze. Per esempio, permette di creare una firma digitale che può essere usata solo con la nostra chiave privata e tuttavia può essere controllata da chiunque abbia la nostra chiave pubblica. Con computer sempre più veloci, la crittografia RSA è ora disponibile, assai opportunamente, come insieme di funzioni software. Computer dedicati sono stati in grado sin dal 1998 di estrarre chiavi DES in pochi giorni di ricerca. DES è stato sostituito da AES, uno standard nuovo e più complesso, dotato di chiavi molto più grandi, per uso commerciale ad alta larghezza di banda. In futuro il beneficio più importante di RSA e dei metodi di crittografia sarà la privacy nella comunicazione personale, oltre alla sicurezza nelle transazioni finanziarie.

La teoria dei numeri, da cui RSA dipende, è sottile e diversa dalla matematica computazionale e dagli algoritmi di rete sui quali si è concentrata inizialmente la computer science. La definizione dei codici di crittografia e la costruzione di sistemi affidabili hanno introdotto alcuni concetti nuovi nella complessità computazionale, portando a una maggiore considerazione della natura delle dimostrazioni e delle verifiche e infine alla scoperta che una verifica può essere effettuata senza comunicare informazione in modo diretto.

Un approccio efficace per verificare che un numero è primo risale a Pierre de Fermat, che nel 1640 affermò (senza fornire quella dimostrazione, che Leibniz e Leonhard Euler avrebbero trovato in seguito) che per ogni intero primo, p, e per ogni numero a che sia relativamente primo con p (per es., 1〈a〈p), si ha:

[13] a^p ≡ a (mod p)

o equivalentemente

[14] a^p₋¹ ≡ 1(mod p).

Per dimostrare le [13] e [14], si consideri il prodotto dei primi p−1 multipli di a:

[15] a×2a×3a×…× (p−1)a=

= (p−1)! a^p−1 (mod p).

I numeri prodotti dalla sequenza a primo membro della [15] sono tutti distinti per via dell’operazione di modulo, cosicché il loro prodotto è anche congruo a (p−1)! (mod p); ne segue a^p₋¹ ≡1 (mod p).

Si noti che l’inverso di questo teorema non è sempre vero: ci sono numeri composti, q, tali che risulta a^q−1≡1 (mod q) per qualche a. Ciò si può verificare ricalcolando la [14] con differenti valori di a; si troverebbero così alcuni numeri composti molto rari (i numeri di Carmichael) per i quali a^q₋¹≡1 (mod q) per ogni a che non sia fattore di q (il più piccolo di questi numeri q è 561=3×11×17). Test di primalità particolarmente ingegnosi sono stati eseguiti da Robert Solovay e Volker Strassen nel 1977 e da Michael O. Rabin nel 1976 e nel 1980. Essi sceglievano a caso il numero a e utilizzavano metodi che evidenziavano efficientemente i fattori composti per garantire che, verificata la [13], la probabilità che p non sia primo non superasse 0,25. Con tali metodi (basati su algoritmi iterati ca. 1000 volte) è stata dimostrata l’esistenza di numeri (industrial strength prime numbers) i quali hanno probabilità inferiore a 4⁻¹⁰⁰⁰ di essere composti e che potrebbero in tutta sicurezza far parte di una chiave privata per la crittografia RSA. Sperimentazioni come i test di primalità hanno introdotto un nuovo tipo di dimostrazione, tendente a provare che una determinata proprietà è vera con probabilità che tende alla certezza; ma, come nel paradosso di Zenone, la certezza non viene mai raggiunta. Nell’ambito della teoria della complessità ciò ha dato vita a una classe di algoritmi polinomiali casuali (o sistemi prova), nei quali la probabilità di smentita (ossia della risposta no) può essere resa arbitrariamente piccola con un’opportuna sequenza di iterazioni. Benché il problema di verificare la primalità si sia effettivamente dimostrato di natura polinomiale, l’algoritmo polinomiale è più lento della migliore ricerca casuale.

Il passo successivo in questa evoluzione è stato la scoperta di un nuovo criterio per la verifica di proprietà dimostrate in modo quasi certo. Ciò ha analogie con alcune caratteristiche della crittografia a chiave pubblica, basate sulla cooperazione del destinatario con il mittente. Si consideri il seguente caso estremo. Qualcuno, che ha trovato un sistema rapido di controllare se due grafi siano isomorfi o meno, desidera convincermi della validità del suo metodo ma non vuole mettermi a conoscenza dei dettagli. Siccome provare o negare l’isomorfismo dei grafi è un problema NP-completo, tale pretesa è improbabile, ma nella moderna computer science teorica torna utile immaginare figure dotate di questo potere, denominate oracoli. Supponiamo che costruiamo due grafi casuali A e B molto grandi, con lo stesso numero di vertici e di spigoli. L’oracolo li studia e assicura che non sono isomorfi; per convincermi, mi chiede di scegliere fra A e B e io, senza fargli sapere quale ho scelto, permuto le etichette dei due grafi. Se il mio interlocutore è veramente un oracolo, può dirmi rapidamente se gli ho dato una variante di A o di B; se invece è un comune mortale, la probabilità che lo possa fare correttamente n volte di seguito è 2⁻ⁿ.

Questo tipo di dimostrazione interattiva è stato discusso per la prima volta nel 1985 da Shafi Goldwasser, Silvio Micali e Charles Rackoff e, da allora, è stata generalizzata ed estesa; utilizzabile sia dai comuni mortali che dagli oracoli, essa ha applicazioni importanti nella crittografia in quanto fornisce approcci distribuiti per verificare affidabilità e sicurezza, attraverso una variante specifica detta dimostrazione a conoscenza zero. Un esempio del procedimento è il seguente: una funzione a senso unico, difficile quanto quella che trova i fattori primi p e q di un numero n=pq, è quella che calcola la radice quadrata di un numero (mod n). Supponiamo che io conosca un numero u la cui radice quadrata (mod n) sia v e che abbia precedentemente, per altra via, già determinato v. Per provare la mia identità desidero convincervi che conosco il valore di u: mandarvi proprio u rivelerebbe il mio segreto e ne invaliderebbe qualsiasi uso futuro; invece scelgo un secondo numero casuale segreto, x, e vi mando

[16] y ≡ x² (mod n).

Ora prendete i=0 o i=1 e chiedetemi di inviarvi z=uⁱx mod(n), che potete controllare verificando che vale la relazione

[17] z² ≡ vⁱy (mod n).

Se non conoscessi u, ma fossi convinto che voi specificherete i=0, potrei mandarvi solo x. Se al contrario ritenessi che voi specificherete i=1, vi invierei un valore falso, y′≡x²/v (mod n) invece di x² (mod n). Quindi se mi chiedete z io vi mando x e il vostro test mostra che x²≡vy′. La mia regola fallisce ogni volta che voi scegliete un valore di i diverso da quello che mi aspetto. La probabilità che in n prove io possa indovinare quale valore di i voi volete specificare e possa rispondere con esito positivo (scegliendo ogni volta un valore diverso di x) senza conoscere il valore di u, è 2⁻ⁿ .

Al contrario dei problemi NP-completi che, in pratica, sono talvolta facili da risolvere, i problemi della teoria dei numeri, come la fattorizzazione di numeri grandi, sono quasi sempre difficili (hard problems). Recentemente tuttavia è stato scoperto che alcuni dei problemi più noti in NP hanno soglie oltre le quali anch’essi diventano quasi sempre hard. Consideriamo una classe particolare di problemi NP-completi, quella dei problemi3-SAT. Un problema 3-SAT è descritto da n variabili binarie e da una formula che consta di m clausole scelte a caso, ognuna vincolante tre variabili. Si tratta di decidere se ci sia qualche configurazione delle n variabili, tale da soddisfare ogni clausola della formula o di dimostrare il contrario. Il rapporto m/n, da mantenere costante al crescere di n e m, costituisce un parametro naturale con cui caratterizzare il problema.

Gli esperimenti al computer hanno mostrato, usando metodi euristici, che esiste un valore di soglia del rapporto m/n, sotto il quale la formula che interviene in un problema 3-SAT (del tipo appena descritto) è quasi sempre soddisfatta e sopra il quale è quasi sempre impossibile da soddisfare. Quando m/n è uguale al valore di soglia i migliori metodi di ricerca euristica sembrano impiegare molto tempo per pervenire alla soluzione del problema; lontano dalla soglia, invece, la maggioranza dei problemi può essere risolta con relativa facilità. Poiché la netta distinzione tra due alternative ben definite (soddisfacimento o meno di tutte le clausole della formula di un problema 3-SAT) è identica a una transizione di fase in fisica, è naturale chiedersi se i metodi della meccanica statistica possano contribuire a far luce su questo argomento. I risultati recenti sono promettenti. Giorgio Parisi, Marc Mézard e Riccardo Zecchina hanno trovato che il valore della soglia può essere previsto molto accuratamente e le loro tecniche sembrano portare a metodi di risoluzione anche dei casi quasi sempre hard, ma è ancora troppo presto per stabilire se tali metodi si possano generalizzare ai molti altri problemi NP-completi. La prossima sfida è individuare il modo di applicarli a problemi della teoria dei numeri.

Con l’inizio del XXI sec., diverse tendenze stanno circoscrivendo i problemi che definiranno la computer science nei decenni a venire. Grazie agli effetti della legge di Moore nel tempo è notevolmente diminuito l’onere iniziale di acquisizione di computer sempre più potenti e, di conseguenza, molte grandi aziende hanno constatato che i fattori principali dei costi di elaborazione sono determinati dal numero di persone necessarie alla manutenzione dei computer e dall’efficienza delle reti telematiche. Al momento sono all’esame tentativi per automatizzare l’amministrazione dei computer come una sorta di ambiente operativo sociale, con slogan quali computer autonomo. La rete in quanto risorsa di calcolo offre nuove prospettive per il parallelismo tra computer condivisi, che si avvantaggia dell’enorme numero di processori collegati tra i computer utilizzati (nella maggior parte dei casi esclusivamente per compiti specifici, come l’elaborazione di testi) e per la straordinaria quantità di memoria disponibile in un tale sistema condiviso.

Le vendite di PC, che ammontano al massimo a 50÷100 milioni di calcolatori all’anno nel mondo, hanno chiaramente raggiunto un punto di stallo, superate da quelle di telefoni cellulari. Di conseguenza alcuni concludono che un ulteriore aumento di coloro che ritengono utile un computer si avrà solamente quando i calcolatori potranno considerarsi alla stregua di elettro-domestici collegati in rete. Da questo punto di vista,considerato che un elettrodomestico svolge bene una sola funzione e offre controlli appropriati soltanto per quella funzione (senza dunque confondere chi lo utilizza, come può invece accadere con un computer), è possibile immaginare calcolatori per scopi specifici sufficientemente economici da venir considerati elettrodomestici.

La legge di Moore, comunque, ci dice che modelli sempre più avanzati di tali elettrodomestici appariranno di anno in anno, caratterizzati da un’obsolescenza ben più rapida di quella degli elettrodomestici tradizionali come il frigorifero o la lavatrice. Mentre molti di noi si sono abituati alla rapida caduta in disuso dei nostri computer, telefoni e automobili, ma è difficile prevedere se l’intera popolazione mondiale sarà disponibile ad acquistare questo tipo di macchine a obsolescenza intrinseca per avere maggiori possibilità di collegamenti o per organizzare il proprio accesso al sapere del mondo.

La fisica del computer: che forma prenderà nel 2100?

Nonostante l’enorme incremento in densità e potenza che si ottiene in base alla legge di Moore e nonostante la miniaturizzazione, i computer di oggi operano secondo gli stessi principî fondamentali della macchina di Turing e dei computer a relè sviluppati negli anni Quaranta nel Regno Unito, negli Stati Uniti e in Germania. Per soddisfare le nostre esigenze di calcolo, entro la fine di questo secolo potrebbero essere impiegate metodologie alquanto diverse. Diventa evidente la necessità di esplorare nuovi modelli di calcolo. Una miniaturizzazione sempre maggiore ci porterà, entro uno o due decenni, al punto in cui un transistor si troverà a occupare un solo atomo. Le potenziali direzioni esplorate sono state avviate da studi sull’elaborazione elettronica che cercano di capirne le caratteristiche fisiche nel senso più generale: se sia soggetta alle leggi della termodinamica; se gli organismi viventi o i processi delle espressioni genetiche elaborino o meno; se un sistema quantomeccanico abbia il potere di calcolare quantità che sono diverse nella loro potenzialità espressiva da quelle ottenibili da un sistema di numeri standard.

Rolf W. Landauer inaugurò il settore della termodinamica dell’elaborazione elettronica in un articolo del 1961, nel quale si domandava se l’irreversibilità di ogni passo di calcolo avrebbe portato inevitabilmente alla generazione di calore. Supponiamo di sommare due bit (mod 2): si comincia con due e si finisce con un bit, senza lasciare alcuna registrazione dei due iniziali. L’idea di Landauer era che tale perdita di informazione è accompagnata dalla generazione di calore in quantità kT (dove k è la costante di Boltzmann e T è la temperatura assoluta del dispositivo che esegue il calcolo). Benché questa sia una minuscola quantità di calore con nessuna conseguenza pratica rispetto ad altre perdite di energia elettrica, Charles H. Bennett mostrò nel 1973 che la si può ridurre a un valore arbitrariamente piccolo eseguendo il calcolo in maniera reversibile. In effetti non occorre cancellare i bit di input, essendo possibile copiarli in un nastro storico, da cui si possa in seguito eseguire il calcolo inverso. John J. Hopfield nel 1974 e Jacques Ninio nel 1975 si accorsero che copiare materiale genetico dalle sottocatene del DNA agli RNA messaggeri per la produzione di proteine era un calcolo reversibile. Nelle cellule, il tornaconto del calcolo reversibile sembra essere l’accuratezza, una sorta di correzione di bozze cinetica che sacrifica l’efficienza alla diminuzione dell’ordine di grandezza della frequenza di errore. Gli sforzi successivi hanno identificato molti eventi che accadono in biochimica e hanno uno spettacolare potere di elaborazione, dovuto al fatto che le trasformazioni chimiche avvengono in parallelo in molte parti di una molecola. Finora, comunque, non è emerso nessun modello di calcolo reversibile o biochimico confrontabile per generalità e facilità di uso con la programmazione nei computer attuali.

L’interesse per le capacità di calcolo da parte di sistemi quantomeccanici semplici è stato stimolato da due direzioni. Nel 1982 Richard P. Feynman ipotizzò che, poiché gli algoritmi di calcolo convenzionali impiegati per simulare l’evoluzione di sistemi quantistici sono estremamente complessi e lenti, sarebbe meglio isolare semplicemente e controllare i sistemi quantistici stessi, in modo tale che i loro stati possano simulare il comportamento di fenomeni quantistici più complessi. Poi, nel 1994, Peter W. Shor mostrò che un computer che esegua procedure quantistiche può fattorizzare numeri grandi in un tempo subesponenziale. Poiché le procedure quantistiche non si trasformano l’una nell’altra allo stesso modo degli algoritmi classici, tale constatazione non è però sufficiente per dimostrare che un siffatto computer è in grado di risolvere tutti i problemi NP-completi in un tempo subesponenziale; tuttavia essa ha portato a un’esplosione di interesse per il calcolo quantistico che continua ancora oggi. Si sono sviluppati metodi di ricerca e crittografia quantistica e di comunicazione mediante codici quantistici correttori di errori. Il calcolo quantistico si svolge in tre passi: (a) inizializzare un sistema quantistico in uno stato noto dei suoi potenzialmente molti gradi di libertà; (b) permettere a esso di evolvere mentre interagisce con fattori esterni che non distruggano la sua coerenza interna; (c) fare una misura che distrugga lo stato quantistico riducendolo a numeri classici. Il testo di Michael A. Nielsen e Isaac L. Chuang fornisce un panorama generale molto chiaro e dettagliato di questo settore in rapida evoluzione. In questo contesto ci sono ovviamente problemi per trovare il modo di esprimere i calcoli generali facili da programmare e ancora più importante è il fatto che è difficile mantenere un sistema quantomeccanico isolato da interazioni non volute con l’ambiente esterno abbastanza a lungo da completare un calcolo. Ciononostante si è potuto eseguire il calcolo quantistico con pochi bit quantistici (qubit) ed è stata ottenuta la comunicazione quantistica crittografata a distanza di molti chilometri. Con l’incremento di un qubit o due all’anno entro pochi decenni ci sentiremo obbligati a sostituire la crittografia RSA con una tecnica completamente quantomeccanica.

Bibliografia

Agrawal 2002: Agrawal, Manindra - Kayal, Neeraj - Saxsena, Nitin, Primes is in P, http://www.cse.iitk.ac.in/news/primality.html.

Aho 1974: Aho, Alfred V. - Hopcroft, John E. - Ullman, Jeffrey D., The design and analysis of computer algorithms, Boston, Addison-Wesley, 1974.

Bennett 1973: Bennett, Charles H., Logical reversibility of computation, “IBM Journal of research development”, 17, 1973, pp. 525-532.

Bennett, Landauer 1985: Bennett, Charles H. - Landauer, Rolf W., Fundamental physical limits of computation, “Scientific American”, 253, 1985, pp. 48-56.

Ceruzzi 1998: Ceruzzi, Paul E., A history of modern computing, Cambridge (Mass.), Massachusetts Institute of Technology Press, 1998.

Codd 1970: Codd, Edgar F., A relational model of data for large shared data banks, “Communications of the Association for Computing Machinery”, 13, 1970, pp. 377-387.

Cook 1971: Cook, Stephen A., The complexity of theorem proving procedures, “Proceedings of the third Association for Computing Machinery symposium on theory of computing”, 1971, pp. 151-158.

Cormen 2001: Cormen, Thomas H. e altri, Introduction to algorithms, 2. ed., Cambridge (Mass.), Massachusetts Institute of Technology Press, 2001 (1. ed.: 1990).

Date 2000: Date, Christopher J., An introduction to database systems, 7. ed., Reading (Mass.) - Harlow, Addison-Wesley, 2000 (1. ed.: Reading (Mass.) - London, Addison-Wesley,1975).

Diffie, Hellmann 1976: Diffie, Whitfield - Hellmann, Martin E., New directions in cryptography, “IEEE Transactions on information theory”, IT-22/6, 1976, pp. 644-654.

Garey, Johnson 1979: Garey, Michael R. - Johnson, David S., Computers and intractability: a guide to the theory of NP-completeness, New York, Freeman, 1979.

Goldwasser 1989: Goldwasser, Shafi - Micali, Silvio - Rackoff, Charles, The knowledge complexity of interactive proof systems, “SIAM Journal of computing”, 18, 1989, pp. 186-208.

Hopfield 1974: Hopfield, John J., Kinetic proofreading: a new mechanism for reducing errors in biosynthetic processes requiring high specificity, “Proceedings of the National Academy of Science”, 71, 1974, pp. 4135-4139.

Hopfield 1980: Hopfield, John J., The energy relay: a proofreading scheme based on dynamic cooperativity and lacking all characteristic symptoms of kinetic proofreading in DNA replication and protein synthesis, “Proceedings of the National Academy of Science”, 77, 1980, pp. 5248-5252.

Huffman 1952: Huffman, David A., A method for the construction of minimum-redundancy codes, “Proceedings of the Institute of Radio Engineers”, 40, 1952, pp. 1098-1101.

Karp 1972: Karp, Richard M., Reducibility among combinatorial problems, in: Complexity of computer calculations, edited by Raymond E. Miller and James W. Thatcher, London, Plenum Press, 1972, pp. 85-103.

Kirkpatrick 1983: Kirkpatrick, Scott - Gelatt, C.D. jr - Vecchi, M.P., Optimization by simulated annealing, “Science”, 220, 1983, pp. 671-680.

Knuth 1997-1998: Knuth, Donald E., The art of computer programming, 3. ed., Reading (Mass.) - Harlow, Addison-Wesley, 1997-1998, 3 v. (1. ed.: 1968).

Landauer 1961: Landauer, Rolf W., Irreversibility and heat generation in the computing process, “IBM Journal of research development”, 5, 1961, pp. 183-191.

Mézard 1987: Mézard, Marc - Parisi, Giorgio - Virasoro, Miguelangel, Spin-glass theory and beyond, Singapore, World Scientific, 1987.

Mézard 2002: Mézard, Marc - Parisi, Giorgio - Zecchina, Riccardo, Analytic and algorithmic solutions of random satisfiability problems, “Science”, 297, 2002, pp. 812-815.

Nielsen, Chuang 2000: Nielsen, Michael A. - Chuang, Isaac L., Quantum computation and quantum information, Cambridge, Cambridge University Press, 2000.

Ninio 1975: Ninio, Jacques, Kinetic amplification of enzyme discrimination, “Biochimie”, 57, 1975, pp. 587-595.

Pennebaker, Mitchell 1993: Pennebaker, William B. - Mitchell, Joan L., JPEG Still image data compression standard, Princeton, Van Nostrand Reinhold, 1993.

Rabin 1980: Rabin, Michael O., Probabilistic algorithm for testing primality, “Journal of number theory”, 12, 1980, pp. 128-138.

Rivest 1978: Rivest, Ronald L. - Shamir, Adi - Adleman, Leonard, A method for obtaining digital signatures and public-key cryptosystems, “Communicatons of the Association for Computing Machinery”, 21, 1978, pp. 120-126.

Shannon 1948: Shannon, Claude E., A mathematical theory of communication, “Bell system technical journal”, 27, 1948, pp. 379-423; 623-656.

Solovay, Strassen 1977: Solovay, Robert - Strassen, Volker, A fast Monte-Carlo test for primality, “SIAM Journal of computing”, 6, 1977, pp. 84-85.

Tarjan 1983:Tarjan, Robert E., Data structures and network algorithms, Philadelphia, Society for Industrial and Applied Mathematics, 1983.

Ziv, Lempel 1977: Ziv, Jacob - Lempel, Abraham, A universal algorithm for sequential data compression, “IEEE Transactions on information theory”, 23, 1977, pp. 337-342.

Ziv, Lempel 1978: Ziv, Jacob - Lempel, Abraham, Compression of individual sequences via variable-rate coding, “IEEE Transactions on information theory”, 24, 1978, pp. 530-536.

Tavola I

Il codice morse e una codifica di huffman

tabella

Esaminiamo il codice Morse per l’alfabeto inglese alla luce della teoria dell’informazione di Shannon e della prescrizione di Huffman per la costruzione di un codice basato sulla frequenza. La seconda colonna della tabella elenca le frequenze di ogni lettera in un testo campione. La terza colonna contiene il codice Morse in punti e linee per ogni carattere. Il tempo in battute impiegato per trasmettere un carattere con il telegrafo si misura colcolando che un punto impiega un battito, una linea due battiti e tenendo presente che le lettere sono separate da un battito. Le lunghezze risultanti sono date nella colonna successiva della tabella. La lunghezza media delle lettere del codice Morse in battiti è 4,51; si tratta di una media ponderata con pesi uguali alle frequenze delle lettere.

figura

Costruiamo poi un albero binario per rappresentare la frequenza delle lettere. Si richede di trovare le lettere di minor frequenza e accoppiarle. Supponiamo che Z capiti tre volte e Q cinque volte; sommiamo le loro frequenze e trattiamo la coppia come se fosse un nuovo carattere dell’alfabeto con peso uguale alla somma, in questo caso 8. La stessa procedura conduce alla coppia J e X, con peso totale 13. Ogni coppia pesa meno della lettera successiva K e pertanto combiniamo le coppie in un nuovo oggetto di peso 21, che poi combiniamo con K, costruendo in questa maniera un albero binario dal basso verso l’alto. Il risultato è mostrato nella figura. Per formare un codice

di Huffman si legge il percorso lungo l’albero dalla radice a ogni lettera, trattando un passo verso sinistra (linee verdi in figura) come uno 0 e un passo verso destra o verso l’alto (linee rosse in figura) come un 1. Per esempio il codice per E è 100; per decodificarlo si tracciano percorsi sull’albero estraendo ogni lettera. Non è necessario inserire pause fra le lettere – come richiedeva il codice Morse – perché quello di Huffman è un cosiddetto codice prefisso, cioè nessun codice è il prefisso di un codice relativo a un’altra lettera. L’ultima colonna della tabella riporta la lunghezza del codice Huffman; la loro media ponderata è 4,15.

Il tasso minimo per un codice permesso dai dati è la sua entropia, definita come il valore atteso (la media su tutti i

simboli, pesati con la loro probabilità di occorrenza p) di log2 (p). Calcolandolo per i simboli e le frequenze, nella tabella si trova che l’entropia dell’insieme di dati è 4,13 e ciò fornisce un limite inferiore per il numero di bit per simbolo. Il codice di Huffman è dunque molto vicino a quello ottimale, come ha dimostrato Shannon. Il codice Morse risulta anch’esso piuttosto efficace e, avendo una lunghezza massima di quattro caratteri, è più facile da memorizzare rispetto alle stringhe lunghe fino a dieci bit richieste dalla procedura di Huffman; quest’ultima, tuttavia, è certamente più idonea all’uso nel campo dei computer.