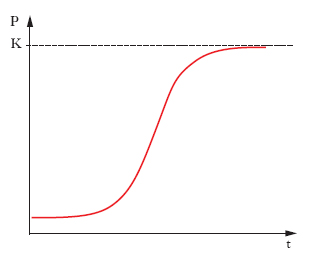
logistica, curva
In statistica, curva ideata da P.F. Verhulst nel 1838 (e successivamente rielaborata e generalizzata da R. Pearl e L.J. Reed) per rappresentare con notevole approssimazione la legge di evoluzione di una popolazione (e in genere di una specie vivente) in base alle ipotesi che da una parte la popolazione tenda, rispetto al tempo, a moltiplicarsi in progressione geometrica e che d’altra parte a tale sviluppo si opponga una resistenza (costituita principalmente dalla limitazione dei mezzi di sussistenza) direttamente proporzionale al quadrato della popolazione. La funzione rappresentata dalla curva (funzione logistica) ha l’espressione P(t)=K/(1+Ce–ht), ove K, C e h sono costanti, t è il tempo. Se le costanti K, C, h sono positive (funzione logistica limitata), la grandezza P(t), all’aumentare del tempo, tende asintoticamente al valore finito K (fig.).