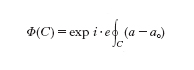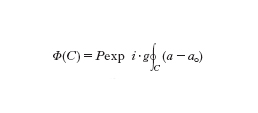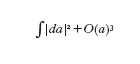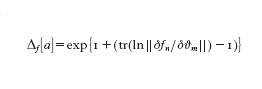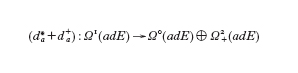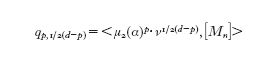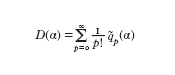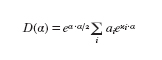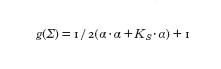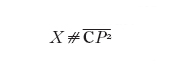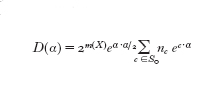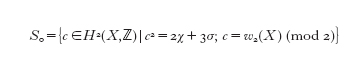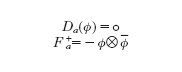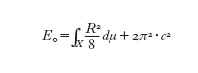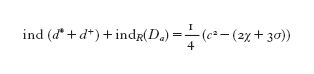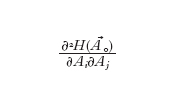Fisica matematica
Fisica matematica
L'interazione fra fisica e matematica è divenuta ancora più proficua negli ultimi anni. Nelle ricerche sulle interazioni fondamentali (gravitazionali, elettromagnetiche, e le interazioni elementari forti e deboli della fisica della particelle), e sull'avvincente questione della loro possibile unificazione (v. App. V, v, p. 645), sono stati adoperati strumenti matematici provenienti dai più svariati settori, come la geometria algebrica, la teoria delle rappresentazioni dei gruppi o la topologia differenziale (v. stringa, App. V, v, p. 307). In questo contesto svolge un ruolo fondamentale il concetto di simmetria, collegato a quello di invarianza (v. fisica, App. IV, i, p. 812; campi, teoria dei, App. IV, i, p. 347; simmetria, App. V, iv, p. 763): nel seguito si approfondisce il tema delle teorie di gauge, teorie di campo basate su una simmetria locale, detta simmetria di gauge, che a loro volta hanno permeato numerosi studi in settori quali la geometria differenziale e le equazioni differenziali. Si registrano inoltre molti sviluppi in settori classici della f. m., come la meccanica, in cui trovano applicazione le teorie delle equazione differenziali ordinarie e alle derivate parziali. Un buon esempio è fornito dal teorema di Kolmogorov, che ha risolto un annoso problema sul moto dei pianeti, ma si rivolge in un senso più generale al problema centrale della non linearità (v. anche equazioni, sistemi dinamici, complessità: Sistemi complessi, in questa Appendice). *
Teorie di gauge
di Andrei Tjurin
Il fondamento della moderna fisica delle particelle elementari è costituito dalle 'teorie di gauge', vale a dire da teorie di campo le cui equazioni risultano invarianti per trasformazioni di gauge (dette in italiano ricalibrature). Come la teoria della gravità si basa sul principio della relatività generale, così le teorie di gauge si fondano sul principio secondo cui la fisica non deve dipendere dal modo in cui è descritta. Nella sua forma più semplice, l'invarianza di gauge si riferisce al fatto che le grandezze misurabili in elettrostatica, come il campo elettrico, non dipendono dal valore assoluto del potenziale elettrostatico ma dalla differenza tra i potenziali di due punti, per cui, aggiungendo un valore costante ai potenziali, ossia 'ricalibrandoli', il campo elettrico rimane invariante.
L'elettromagnetismo come teoria di gauge
L'elettromagnetismo è stato un punto di partenza per le teorie di gauge locali, e più precisamente per la dinamica di una particella quantizzata carica che si muove in un campo elettromagnetico classico. Un campo abeliano (elettromagnetico classico) su un certo dominio dello spazio-tempo Ω è dato da una connessione unitaria a ('potenziale di gauge') su un fibrato di rette L a meno dell'azione del gruppo degli automorfismi unitari ('gruppo delle trasformazioni di gauge') del suddetto fibrato L ('invarianza locale di gauge'). Se il dominio Ω è semplicemente connesso allora il campo elettromagnetico è determinato in modo univoco dal tensore di curvatura Fa della connessione a, il quale è una 2-forma differenziale su Ω (il tensore di campo elettromagnetico). Una connessione a su L è data da un operatore differenziale lineare del primo ordine sullo spazio delle sezioni di L con il differenziale ordinario come simbolo principale (derivata covariante); così la differenza fra una coppia di connessioni è una 1-forma differenziale su Ω. È possibile fare la combinazione convessa di connessioni e perciò lo spazio di tutte le connessioni su L è uno spazio affine nello spazio delle 1-forme.
In particolare, se il dominio Ω è semplicemente connesso, se L è banale e ammette una particolare connessione banale a₀ allora qualsiasi altra connessione a può essere data in modo unico come una 1-forma differenziale ω=a−a₀; questa è l'espressione tradizionale con cui si indica il potenziale di un campo elettromagnetico. Nella fisica classica il campo elettromagnetico viene definito in ogni punto del dominio come la forza che una carica classica (per es. un elettrone) subirebbe inizialmente se posta in quel punto; quindi un campo è definito tramite il tensore di curvatura (il tensore dell'intensità del campo) del potenziale, secondo quanto concepito da M. Faraday e J.C. Maxwell. Tuttavia il potenziale è stato considerato a lungo una quantità sussidiaria introdotta per rendere più convenienti le manipolazioni matematiche. Nella teoria quantistica invece gli elettroni sono descritti tramite una funzione d'onda con una fase che dipende dal potenziale di gauge del dominio. Questo è stato dimostrato dal fondamentale esperimento proposto da Y. Aharonov e D. Bohm nel 1959 ed effettuato con successo per la prima volta da R.G. Chembers nel 1960.
La struttura di quest'esperimento è estremamente semplice: agli elettroni emessi da un'unica sorgente si consente di passare da uno qualsiasi dei due lati di un nucleo magnetizzato; proseguendo nel loro cammino le particelle interferiscono con uno schermo che si trova a una certa distanza. Il campo magnetico è ristretto nel dominio all'interno del nucleo (vicino al suo centro) così che nella regione attraversata dagli elettroni il tensore del campo è identicamente nullo. Nello schema della meccanica classica non dovrebbe verificarsi alcuna interazione tra gli elettroni e il campo. Ma nella teoria quantistica invece la fase della funzione d'onda di un elettrone dipende dal potenziale di gauge: la differenza di fase ottenuta sullo schermo tra gli elettroni che vi arrivano seguendo i due cammini differenti, relativi ai differenti lati del nucleo, è esattamente il flusso magnetico totale che passa attraverso il nucleo. Così la fase relativa nello stesso punto in un dominio dello spazio-tempo è una quantità fisica osservabile, perché elettroni che arrivano nello stesso punto dello schermo lungo i due cammini relativi ai lati differenti del nucleo interferiranno costruttivamente o distruttivamente a seconda che essi siano in fase o fuori fase, come si può calcolare tramite la formula del flusso magnetico totale che scorre attraverso il nucleo. La validità di tale formula è stata mostrata da Chembers e altri in una grande varietà di condizioni sperimentali (Aharonov, Bohm 1959).
Il risultato positivo di questo famoso esperimento è la più forte conferma sperimentale del principio basilare che vede l'elettromagnetismo come teoria di gauge. Così la conoscenza del tensore del campo elettromagnetico Fa attraverso il dominio Ω percorso dagli elettroni è insufficiente per determinare la fase della funzione d'onda dell'elettrone. Quindi la variabile dinamica data dal tensore Fa sotto-descrive la teoria quantistica di una particella carica che si muove in un campo elettromagnetico. Si può dimostrare che è sufficiente aggiungere il potenziale di gauge a come variabile dinamica per ottenere una descrizione completa dei fenomeni fisici; tuttavia a presenta lo svantaggio di sopra-descrivere il sistema, nel senso che valori differenti di a possono corrispondere alle medesime condizioni fisiche. In effetti, nell'esperimento di Aharonov-Bohm, facendo agire il gruppo di gauge si ottiene lo stesso valore per la differenza di fase e quindi le stesse figure di diffrazione sullo schermo. Va sottolineato che, in realtà, persino la differenza di fase non è propriamente una quantità osservabile: se essa cambiasse di un multiplo intero di 2π le figure di diffrazione resterebbero ancora immutate. In altre parole essa non è gauge-invariante. Ciò che è fisicamente osservabile nell'esperimento di Aharonov-Bohm è il fattore di fase di Dirac:
dove l'integrale di linea nell'esponente è considerato lungo una curva chiusa C come, per es., una circonferenza intorno al nucleo (in questa formula e rappresenta la carica dell'elettrone). Diversamente da a e da Fa, questo fattore esprime correttamente l'effetto di fase della funzione d'onda dell'elettrone. Di conseguenza, se fissiamo il tensore di campo Fa, lo spazio dei parametri nascosti per l'effettiva descrizione esatta dei fenomeni fisici quantistici è il toro H¹(Ω,R)/H¹(Ω,Z) dove H¹(Ω,R) è il gruppo di coomologia del dominio Ω a coefficienti reali e H¹(Ω,Z) quello a coefficienti interi.
Le teorie di gauge non-abeliane e la loro struttura matematica
Il principio dell'invarianza locale di gauge è stato esteso dal semplice prototipo dell'elettrodinamica quantistica con gruppo di gauge abeliano a quello più generale di un gruppo di gauge non abeliano. Tale estensione è stata proposta da C.N. Yang e R.L. Mills nel 1954 allo scopo di costruire un modello per l'interazione delle particelle elementari: oggi è chiaro che questa teoria descrive con successo, all'interno della teoria quantistica dei campi, le interazioni forti dei quark e le forze elettrodeboli dei quark (v. App. V) e dei leptoni (v. App. V) (Yang, Mills 1954). Lo sviluppo fisico delle procedure di quantizzazione per i campi di gauge non abeliani tramite le importanti regole di Feynman, così come la rinormalizzazione perturbativa, mostra che la teoria non abeliana è più sottile del prototipo abeliano, cioè dell'elettrodinamica quantistica. La versione corretta di tali procedure fu proposta da B.S. De Witt, D. Faddeev e V. Popov nel 1967. In particolare l'unitarietà perturbativa richiede l'introduzione di particelle fermioniche fittizie (particelle 'fantasma') di spin zero. Inoltre, a causa del teorema di Goldstone, la simmetria globale implica l'esistenza di particelle scalari prive di massa la cui presenza è indesiderabile da un punto di vista fenomenologico. Fortunatamente il cosiddetto meccanismo della rottura spontanea della simmetria di gauge evita questo problema, come è stato mostrato da P. Higgs nel 1964. Nel 1971 G.'t Hooft ha fatto vedere che questo meccanismo non distrugge la rinormalizzabilità della teoria; nel decennio successivo è stato costruito un modello consistente che, usando SU(2)×U(1) come gruppo di gauge, unifica l'interazione elettromagnetica e l'interazione debole, come era stato previsto da S.L. Glashow nel 1960. Il meccanismo di Higgs è stato aggiunto a questa teoria da S. Weinberg e A. Salam nel 1967. Il modello prevedeva l'esistenza di correnti deboli neutre la cui forza di accoppiamento e le cui proprietà di trasformazione fossero definite: tali correnti sono state scoperte al CERN nel 1973 e controllate in dettaglio allo SLAC (Standford Linear Accelerator Center) nel 1978. Questo successo è stato riconosciuto con il premio Nobel attribuito a Glashow, Salam e Weinberg nel 1979. Nel 1983 sempre al CERN si è dimostrato che i bosoni W e Z hanno le masse previste: per questa scoperta C. Rubbia e S. van der Meer hanno condiviso il premio Nobel nel 1984 (v. fisica nucleare, App. V). A livello più congetturale resta un'altra applicazione delle teorie di gauge alle interazioni forti: la cromodinamica quantistica (v. App. V) basata su SU(3) è stata considerata accettabile a causa della libertà asintotica scoperta da G. 't Hooft, B.D. Politzer, D.J. Gross e F. Wilczek nel 1973. Tale proprietà spiega le peculiarità dell'accoppiamento debole dei quark a breve distanza (≤10⁻¹⁴ cm) e conduce al confinamento dei quark a distanze 'grandi' (intorno a 10⁻¹³ cm), comportamento che è stato fortemente suggerito dagli studi fatti da Creutz e altri con l'ausilio del computer, usando il reticolo spazio-temporale discretizzato suggerito da K.G. Wilson nel 1974. Infine l'argomento più congetturale resta la grande unificazione alle basse energie per SU(3)×SU(2)×U(1), la quale richiede un gruppo più grande (per es. SU(5), come proposto da H. Georgi e Glashow nel 1974). Quest'unificazione non prevede alcun aspetto fisico nuovo tra 100 GeV e 10¹⁴ GeV. Attualmente nessuna previsione di queste teorie, a parte quella dell'angolo di miscelamento elettrodebole, è stata confermata sperimentalmente.
Nelle teorie di gauge non abeliane il fibrato di rette L è sostituito da un fibrato vettoriale Eh di rango elevato dotato di una struttura hermitiana h. Una fibra di Eh su un qualsiasi punto spazio-temporale è uno spazio interno, e per cambiamento di fase si intende un cambiamento in uno spazio interno tramite una trasformazione unitaria arbitraria. Nella teoria di Yang-Mills originaria Eh è di rango due e il gruppo di trasformazione locale è SU(2), poiché essa era stata proposta per descrivere le forze che mettono in relazione i nucleoni (protoni e neutroni), i quali non vengono distinti rispetto all'accoppiamento forte tramite invarianza isotopica. Più generalmente, in fisica si è soliti chiamare con il nome di gruppo di gauge il gruppo di simmetria G di uno spazio interno e con il nome di gruppo delle trasformazioni di gauge il gruppo infinito-dimensionale S delle funzioni che vanno dallo spazio-tempo a G; in un contesto matematico tali gruppi sono detti rispettivamente gruppo di struttura e gruppo di gauge. Di conseguenza la differenza tra due connessioni (a−a₀) è una 1-forma differenziale con coefficienti nell'algebra di Lie di G e il tensore di curvatura è una 2-forma differenziale a coefficienti nella stessa algebra. La funzione F:A(Eh)→Ω²(adE) dallo spazio delle connessioni allo spazio delle 2-forme (la quale associa la forma di curvatura alla connessione) è una funzione equivariante rispetto al gruppo delle trasformazioni di gauge S che agisce per trasformazioni aggiunte sulle algebre di Lie.
Nel caso non commutativo la procedura del trasporto parallelo lungo un cammino arbitrario è un po' più complicata: per convenzione si scrive ancora simbolicamente il risultato del trasporto parallelo lungo un cammino γ come Pexpi∙g∫γ (a−a₀), dove P denota l'orientamento lungo il cammino (path-ordering). In effetti il trasporto parallelo può essere considerato come il prodotto degli esponenziali lungo i segmenti infinitesimali, ordinati da destra a sinistra mentre ci si muove lungo il cammino γ. Ora il fattore di fase path-ordered lungo un laccio chiuso C
possiede le proprietà richieste alle osservabili fisiche, analogamente al fattore di fase di Dirac; a volte ci si riferisce a questo fattore, nel suddetto contesto, come al laccio di Wilson. La dipendenza di gauge relativa al punto iniziale (o al punto finale) può essere rimossa considerando la traccia del fattore di fase. Nel linguaggio matematico questo fattore di fase è l'olonomia della connessione a lungo C. Nel caso non commutativo il fattore di fase non è l'esponenziale dell'integrale di linea e questa differenza con l'elettromagnetismo risulta fondamentale. In particolare, non sembra esistere alcuna generalizzazione utile del concetto elettromagnetico di flusso all'interno della teoria di Yang-Mills. Inoltre, per quanto riguarda la teoria elettrodebole e la cromodinamica le condizioni fisiche non rendono possibile, fino a ora, concepire e realizzare alcun esperimento del tipo Aharonov-Bohm.
Topologia e monopoli
Nel 1931 P. Dirac osservò una delle caratteristiche più affascinanti delle teorie di gauge: l'apparire naturale in esse di monopoli come ostruzioni topologiche. Nell'elettrodinamica un monopolo magnetico è equivalente, come ostruzione topologica, alla sua definizione convenzionale di sorgente del flusso magnetico. Sia S una superficie nel dominio Ω descritta da una famiglia di lacci chiusi {Ct} parametrizzati dalla variabile t∈[0,2π] tale che C₀=C₂π=p₀ è un punto fissato. Al variare di t in modo continuo tra 0 e 2π i fattori di fase di Ct descrivono un laccio continuo γ nel gruppo di gauge U(1). Se la classe di omotopia [γ]∈π₁ (U(1))=Z è non banale, allora otteniamo un monopolo all'interno della superficie S. È facile calcolare il flusso magnetico totale attraverso S: se [γ]=n (si ricordi l'isomorfismo π₁(U(1))=Z) allora il flusso magnetico totale che emerge da S è 2π∙n/e; questo significa che la carica magnetica contenuta in S è ẽ=n/2∙e dove e, come al solito, è il valore assoluto della carica elettrica dell'elettrone. Così la carica magnetica non può prendere valori diversi dai multipli interi di 1/2∙e. Il risultato è la famosa condizione di quantizzazione di Dirac. Da questo si può dedurre che la carica magnetica quantizzata è una quantità conservata sia nella dinamica classica sia nella dinamica quantistica.
La descrizione matematica di questo fenomeno è la seguente: un fibrato di rette L dotato di una norma hermitiana h definisce un unico fibrato di circonferenze su Ω la cui restrizione a S è non banale se S contiene un monopolo; la carica magnetica è la classe caratteristica del fibrato di circonferenze. Con argomentazioni dello stesso tipo si possono ottenere monopoli non abeliani come ostruzioni topologiche per ogni gruppo di gauge non abeliano G che abbia gruppi di omotopia non banali; gli elementi di tali gruppi corrispondono ad altri tipi di cariche. Per definizione queste nuove cariche sono discrete e sono anche, in un certo senso, quantizzate: perciò si tratta nuovamente di quantità conservate.
In certe teorie non abeliane, con rottura spontanea di simmetria (v. oltre), possono esistere soluzioni che trasportano cariche di monopolo, come i solitoni di t'Hooft-Polyakov (1974) nella teoria SO(3). Essi sono semplicemente monopoli U(1) immersi in una teoria con un gruppo di gauge più grande. Questi solitoni carichi magneticamente sono U(1)-sottofibrati (abeliani, topologicamente non banali) di un SO(3)-fibrato banale ma non abeliano. Per descrivere il meccanismo matematico di esistenza di solitoni di tipo-monopolo si consideri una lagrangiana relativa a una connessione e a un campo ausiliario su R³ con una G-orbita G/H come minimo della funzione potenziale U e si assumano opportune condizioni di finitezza asintotiche in R³. In tal caso i valori all'infinito del campo danno una mappa dalla 2-sfera all'orbita G/H la quale si suppone essere topologicamente non banale, e la classe di omotopia appare quindi come una specie di carica topologica del sistema. Nello spazio-tempo quadrimensionale lo *-operatore di Hodge agisce sulle 2-forme come un'(anti)involuzione. In questo caso, per il lemma di Poincaré, il campo di gauge Fa definisce un nuovo campo di gauge *Fa . Un monopolo del campo di Maxwell Fa si può anche considerare come una sorgente del campo di Maxwell duale *Fa nello stesso senso in cui una carica elettrica viene considerata come una sorgente del campo di Maxwell Fa. Così una carica elettrica può anche essere considerata come un monopolo del campo duale *Fa . Ora la definizione topologica di una carica di monopolo è essa stessa sufficiente a determinare l'interazione monopolo-campo e conduce a un unico insieme di equazioni del moto in ognuno dei casi classico e quantistico; si tratta delle equazioni di Maxwell e di Lorentz per una sorgente che furono dedotte da Faraday e Maxwell per via sperimentale. Perciò l'interazione della carica con il campo elettromagnetico appare, in modo naturale, unicamente come conseguenza della topologia, senza l'introduzione di concetti fenomenologici.
Una nuova caratteristica del caso quantistico è il fenomeno del raddoppiamento chirale, vale a dire il fenomeno per cui le equazioni del moto posseggono un'invarianza di gauge locale rispetto a delle nuove trasformazioni di gauge e il sistema ha un'invarianza di gauge locale rispetto a U(1)×∼U(1), dove ∼U(1) ha la parità opposta alla copia originale U(1) ed è associato con il potenziale del campo duale *Fa. Questa simmetria duale dell'elettromagnetismo - una simmetria tra il campo e il campo duale, così come tra una sorgente e un monopolo - non può essere estesa alle teorie non abeliane classiche. Per es., sorgenti e monopoli sono in generale oggetti differenti: per una teoria SO(3) le cariche di sorgente sono 'numeri' delle rappresentazioni del gruppo, mentre le cariche di monopolo sono parametrizzate da π₁ (SO(3)) e cioè da un segno. Tuttavia, usando variabili di laccio si può ottenere la simmetria quasi-duale tra le equazioni per i monopoli non abeliani e le equazioni di Wong per una sorgente. La questione riguardante l'esistenza di monopoli dovrebbe essere risolta, in linea di principio, tramite la progettazione di strumenti per rivelare i suddetti tramite esperimenti. Esiste anche un'affascinante possibilità: alcune particelle che già conosciamo potrebbero essere, in effetti, monopoli piuttosto che sorgenti. Tuttavia, il giudizio convenzionale, già sostanziato da un corpo estremamente grande di evidenza sperimentale, è che esse siano tutte sorgenti le quali obbediscono alla dinamica prescritta dalla teoria di Yang-Mills.
Fibrati e rottura spontanea di simmetria
Nelle applicazioni pratiche delle teorie di gauge spesso si ha a che fare con la cosiddetta rottura spontanea di simmetria. Per descrivere l'evoluzione nel tempo di un sistema fisico si deve usare un principio di azione. Per le teorie di gauge l'azione deve essere invariante rispetto alle trasformazioni di gauge locali: per es., nel caso della teoria di Yang-Mills pura si ha
con la connessione a considerata come la variabile con stato fondamentale dato dalla connessione piatta a=0 e con i termini quadratici
in cui compaiono le derivate di a. Perciò la particella corrispondente avrebbe massa zero: si tratta di un 'bosone vettoriale senza massa' che non è desiderato da un punto di vista fenomenologico; è però impossibile scrivere una lagrangiana gauge-invariante con termini quadratici in a piuttosto che nelle sue derivate. Se il campo di gauge è assente e si considerano altri campi (sezioni di fibrati associati), per es. un campo tale che ψ sia una funzione vettoriale complessa e la lagrangiana abbia la forma |∇ψ|²+U(ψ) (dove U è invariante rispetto al gruppo di gauge G), allora lo stato fondamentale è dato da una qualsiasi funzione costante il cui valore sia un minimo di U; perciò la scelta di uno stato fondamentale rompe la G-simmetria. Questa 'rottura spontanea di simmetria' conduce nuovamente a particelle prive di massa non desiderate. Sorprendentemente, questi due problematici fenomeni scompaiono quando si mettono insieme le due situazioni e si va a considerare una lagrangiana che coinvolga una connessione e un campo ausiliario: in tal caso la scelta di uno stato fondamentale produce anche una banalizzazione del fibrato rilevante, la quale assorbe la libertà di gauge. Perciò l'interazione del campo di gauge e del campo ausiliario fornisce alle particelle associate masse non nulle. Si tratta del meccanismo di Higgs (Guralnik, Hagen, Kibble, Englert, Brout) che fornisce il modello di Weinberg-Salam per i leptoni e cioè la versione rinormalizzabile della teoria di Glashow.
Spazio dei moduli e quantizzazione
Per la procedura di quantizzazione di Feynmann delle teorie di gauge non abeliane è molto importante descrivere l'omotopia dello spazio delle orbite o spazio dei moduli delle connessioni: B=Ah/S dove Ah è lo spazio affine delle connessioni hermitiane su cui agisce il gruppo delle trasformazioni di gauge. Un gauge globale o scelta di gauge è una sezione del fibrato Ah→B. Se esistesse una tale sezione allora Ah avrebbe lo stesso tipo omotopico del prodotto diretto G×B il che sarebbe in contraddizione con la contraibilità di Ah. Quest'effetto è noto come ambiguità di Gribov. Tuttavia esistono un certo numero di quasi-sezioni come il gauge di Coulomb dato dalla condizione d*a=0 (oppure div(a−a₀)=0), il gauge di Lorentz o covariante dato dallo stesso tipo di condizione per la metrica pseudo-riemanniana sullo spazio-tempo, il gauge radiale e così via.
Per evitare i nuovi infiniti dell'integrale di Feynman provenienti dal volume infinito di un'orbita si deve usare il trucco di Faddeev-Popov: supponiamo che fn(a),n=1,2,… sia una qualsiasi condizione di gauge fissata, che ϑm siano i parametri del gruppo di gauge G (per es. SU(2)) e che Δf[a]=det||δfn/δϑm||; in tal caso, ponendo nella misura funzionale il moltiplicatore Δf∙δ[f(a)], si possono rimuovere le integrazioni non necessarie. Se ora riscriviamo un determinante come un esponente, cioè come
si può considerare l'esponente della serie di Taylor di ln (1+…) come la decomposizione di laccio associata al campo fantasma fittizio. Così, da un punto di vista tipicamente matematico, il fantasma è la restrizione all'orbita della variazione funzionale logaritmica in S. La restrizione all'orbita della variazione funzionale in Ah definisce l'operatore BRST. La lagrangiana effettiva della quantizzazione non è invariante rispetto alle trasformazioni di gauge ma è invariante rispetto all'operatore BRST. Da questo si può ottenere l'analogo delle identità di Ward, le cosiddette identità di Slavnov-Taylor, le quali mettono in relazione le funzioni di Green; tali identità per le teorie non abeliane sono di gran lunga più forti rispetto a quelle abeliane originali. L'operatore BRST è nilpotente di ordine due, così che le osservabili quantistiche possono essere considerate come classi di coomologia di ordine uno. D'altro lato usando la condizione di consistenza di Wess-Zumino si può calcolare completamente l'anomalia non abeliana tramite il primo termine della condizione. Tutte queste costruzioni sono state usate nella cromodinamica quantistica e nei modelli delle teorie di grande unificazione.
La generalizzazione naturale della teoria di Yang-Mills è la versione supersimmetrica. La procedura di quantizzazione disturba metà delle supersimmetrie date tramite il solo numero N. D'altro lato alcune teorie di questo tipo sono una realizzazione quantistica della classica dualità elettro-magnetica della teoria abeliana di Maxwell. Per es., la dualità di Montonen-Olive della super-teoria di Yang-Mills non abeliana quadrimensionale (N=4) scambia i bosoni di gauge, che tipicamente vengono considerati come campi fondamentali, con i monopoli di t'Hooft-Polyakov, i quali appaiono come soluzioni solitoniche delle equazioni di campo classiche e in tal modo scambiano anche i campi elettrico e magnetico. Se le costanti di accoppiamento duali λ e λD sono poste in relazione da λD=1/λ, cosicché il limite λD→0 corrisponde al limite λ→∞, allora si parla di S-dualità. Questo mette quindi in relazione l'accoppiamento debole λ=0 con l'accoppiamento forte λ=∞. Un esempio tipico di tale dualità nella fisica statistica è dato dalla dualità di Kramers-Wanier nel modello di Ising.
Applicazioni delle teorie di gauge alla geometria in dimensione bassa
di Andrei Tjurin
A partire dal 1982 la teoria di Yang-Mills per le metriche riemanniane è stata applicata con successo a problemi di topologia differenziale delle varietà quadrimensionali che erano aperti da un quarto di secolo. Uno dei principali artefici di questo sviluppo è stato S. Donaldson. La soluzione del problema delle forme di intersezione negative, le strutture lisce esotiche sulle superfici algebriche semplicemente connesse, l'invarianza liscia della classe canonica rappresentano una breve lista delle applicazioni delle teorie di gauge alla topologia differenziale in dimensione quattro. Le applicazioni della teoria di gauge all'interpretazione degli invarianti delle varietà tridimensionali da parte di C. Taubes nel 1990 e la descrizione dell'interazione tra la geometria di gauge nelle dimensioni adiacenti due, tre e quattro scoperte da M.F. Atiyah, Donaldson, N.J. Hitchin e altri hanno messo insieme idee provenienti dalle teorie quantistiche dei campi e hanno svolto un ruolo importante nel fissare le direzioni principali per la ricerca moderna in geometria. Negli ultimi tre mesi del 1994, usando un nuovo tipo di equazione differenziale-geometrica proposta da N. Seiberg e E. Witten, sono stati risolti problemi aperti da molto tempo. Inoltre, sulla base del lavoro iniziale di carattere fisico di Seiberg e Witten sono state trovate dimostrazioni nuove e più semplici di risultati già esistenti; nuove prospettive per la ricerca sono state aperte da vari matematici, specialmente da P. Kronheimer, T. Mrowka, J.W. Morgan, R. Fintushel, R.J. Stern e Taubes.
Sicuramente il risultato più importante e sorprendente è stato la dimostrazione di Donaldson della non-unicità della struttura differenziale su R⁴. Si sapeva infatti che per n≠4 su Rn si può dare un'unica struttura differenziale; era noto cioè che una varietà omeomorfa a Rn (equivalenza topologica) deve essere anche diffeomeorfa a Rn (dotato della struttura differenziale ordinaria). Donaldson ha dimostrato che in dimensione quattro esistono invece delle strutture 'esotiche' e cioè delle varietà che sono omeomorfe a Rn ma non a esso diffeomorfe. Dato che la dimensione quattro è quella del continuum spazio-temporale l'interesse di tale risultato sembra andare al di là dell'ambito matematico. Così, prima della questione riguardante la metrica di Lorentz, nella relatività generale va posta la questione della scelta di una struttura differenziale sulla varietà quadrimensionale sottostante.
Nella topologia differenziale se si ha una famiglia di equazioni alle derivate parziali, dipendente da parametri continui, si possono trovare invarianti di una struttura liscia dalla classe di omologia dello spazio delle soluzioni. Nella struttura della topologia differenziale per le varietà di Banach è necessario stabilire alcuni punti chiave: la linearizzazione delle equazioni intorno a una soluzione dovrebbe essere rappresentata da equazioni differenziali ellittiche lineari. L'indice dell'equazione linearizzata fornisce la 'dimensione attesa' per lo spazio delle soluzioni e, dopo opportune perturbazioni generiche delle equazioni, lo spazio delle soluzioni ha effettivamente la suddetta dimensione. Inoltre è necessario stabilire la compattezza dello spazio delle soluzioni (o un qualche analogo più debole di questo fatto) e l'orientabilità, altrimenti si ottengono solo invarianti modulo 2. Le equazioni sono invarianti sotto l'azione del gruppo di gauge (nella terminologia fisica 'gruppo delle trasformazioni di gauge') degli automorfismi del fibrato: si studiano gli spazi delle soluzioni modulo questa azione. Possono verificarsi delle difficoltà a causa delle soluzioni riducibili, con uno stabilizzatore non banale nel gruppo di gauge. Gli invarianti delle varietà quadrimensionali ottenuti dagli spazi di moduli degli istantoni si adattano a questo schema: per una varietà liscia X e un SU(2)-fibrato E→X con classe di Chern c₂=n e una metrica riemanniana g si studia l'equazione dell'istantone F⁺a=0 per una connessione a su E (dove la decomposizione Fa=F⁺a+F⁻a è data dallo *-operatore di Hodge associato a g) come una famiglia di equazioni alle derivate parziali con parametro [a]. Lo spazio delle orbite delle soluzioni è il cosiddetto spazio dei moduli degli istantanei.
La linearizzazione dell'equazione, modulo l'azione del gruppo di gauge, è presente tramite l'operatore
che è ellittico con indice 8n−3(1−b₁+b⁺₂), dove i numeri bi sono i numeri di Betti e b⁺₂ è la dimensione dello spazio delle forme armoniche autoduali. Se b⁺₂>0 non ci sono soluzioni riducibili per una metrica generica e se b⁺₂>1 non ci sono soluzioni in famiglie a un parametro generiche. Lo spazio dei moduli degli istantoni può essere orientato tramite una scelta di orientazione della retta: ∧t°p(H¹(X))⊗∧t°p(H²⁺). Gli spazi dei moduli Mn non sono compatti ma esiste un'opportuna compattificazione che permette di definire un'appropriata classe fondamentale [Mn] la quale si accoppia con le classi di coomologia date dalle funzioni: μi:Hi(X)→H⁴⁻i(Mn). Assumendo che b₁−b⁺₂ sia dispari si ottengono gli spazi di moduli di dimensione pari 2d e le collezioni di polinomi di Donaldson:
dove α∈H₂(X). Questa collezione di polinomi sul gruppo di coomologia H²(Mn) è definita usando una scelta di una metrica riemanniana X, ma se b⁺₂>1 si ottengono degli invarianti topologici differenziali, indipendentemente dalla metrica. Nel caso b⁺₂=1 il quadro è più complicato; gli invarianti dipendono dalla scelta di una camera: una metrica riemanniana determina una camera nella coomologia X tramite la sua forma armonica autoduale. Gli 'invarianti' cambiano non appena si passa tra le camere a causa dell'apparire di soluzioni riducibili.
Kronheimer e Mrowka hanno introdotto la nozione di varietà quadrimensionale di tipo semplice. Per tali varietà gli invarianti degli istantoni possono essere codificati in un'unica serie (formale) di potenze:
dove ˜qp=qp,₀ se p=b⁺₂+1 (mod2) e ˜qp=1/2qp,₁ altrimenti. I teoremi di struttura di Kronheimer e Mrowka asseriscono che esiste un numero finito di classi - dette classi di base - ϰi∈H²(X) e coefficienti ai∈Q tali che
Usando gli spazi di moduli degli istantoni, Donaldson ha ottenuto una collezione schiacciante di risultati sull'esistenza e unicità di varietà quadrimensionali lisce di dato tipo topologico, le quali sono definite in modo unico dalla forma di intersezione per una varietà semplicemente connessa. Questa forma di intersezione è una forma unimodulare intera su H²(X, Z).
La lista dei risultati principali è la seguente. Le sole forme definite negative realizzate come forme di intersezione di varietà quadrimensionali, compatte, semplicemente connesse, lisce sono le forme diagonalizzabili standard. Perciò nessuna delle forme 'esotiche' (E₈-multipli, il reticolo di Leech, ecc.) potrà mai provenire da varietà quadrimensionali, chiuse e lisce. Se la varietà quadrimensionale X è una somma connessa, orientata, liscia della varietà Xi e se b⁺₂(Xi)>0 allora per ogni polinomio di Donaldson si ha qp,₀=0. Se S è una superficie complessa, semplicemente connessa con b⁺₂>2 allora qp,₀≠0 per p sufficientemente grande. Da questo si possono ottenere un gran numero di strutture lisce esotiche sulle superfici algebriche. Per ogni superficie complessa semplicemente connessa S con b⁺₂>2 esiste una varietà quadrimensionale liscia X(S) omeomorfa ma non diffeomorfa a S né a un'arbitraria superficie complessa. Qui la varietà X(S) (il cosiddetto topomodello di S) viene costruita come somma connessa in modo da avere la stessa forma di intersezione di S.
La successiva area di problemi, in relazione con il problema di Thom, è stata affrontata con successo da Kronheimer e Mrowka: è sempre possibile trovare una superficie orientata liscia Σ, immersa in X, che rappresenta la classe di 2-omologia a, di genere g(Σ) arbitrariamente grande; un problema interessante è quello di trovare il genere minimo di un rappresentante. Una famosa congettura, frequentemente attribuita a R. Thom, prevede che la curva complessa Σ, in una superficie algebrica S minimizza il genere nelle classi di omologia:
dove KS è la classe canonica di S. Kronheimer e Mrowka hanno dimostrato che g(Σ)≥1/2(α∙α+ϰi∙α)+1 per ogni classe di base ϰi e per ogni S di tipo semplice. Per molte superfici complesse si è potuto mostrare che KS è una classe di base dimostrando così la congettura di Thom.
Fintushel e Stern hanno derivato il teorema di struttura per numerose varietà quadrimensionali usando la decomposizione generalizzata come somma connessa X=X₁ YX₂ di una varietà quadrimensionale la quale viene separata in due tramite una varietà tridimensionale Y. Una questione fondamentale era di trovare formule che mettessero gli invarianti di X in relazione con quelli della somma connessa
imitando così la procedura di blow up della geometria algebrica. Fintushel e Stern hanno mostrato che, anche se X non è di tipo semplice, esiste una formula esplicita esprimibile tramite le funzioni ellittiche. La costruzione fondamentale per tale approccio a questo tipo di problemi è la teoria dell'omologia di A. Floer delle varietà tridimensionali, usata da Floer per dimostrare la congettura di Arnold nella geometria simplettica. Questa teoria è uno degli esempi che ha condotto all'idea di una 'teoria topologica dei campi quantistici', la quale è stata sviluppata da Witten nei suoi famosi lavori sui nodi e sugli invarianti delle varietà tridimensionali.
Nel 1993 quest'approccio tramite la teoria dei campi quantistici è stato esteso agli invarianti delle varietà quadrimensionali i quali possono essere interpretati come integrali funzionali, dove l'integrazione avviene sullo spazio delle connessioni di certi campi ausiliari. Infatti gli invarianti sono i valori di attesa naturali in una variante della teoria di Yang-Mills supersimmetrica per N=2. Atiyah e Jeffrey hanno chiarito le formule di Witten ponendole in uno schema generale di geometria differenziale relativo alla teoria di Chern-Weil per la classe di Eulero di un fibrato con una sezione. Quest'interpretazione tramite la teoria quantistica dei campi è soggetta a difficoltà fondamentali relative alla definizione matematicamente rigorosa degli integrali funzionali. Ma l'analisi tramite la teoria quantistica dei campi implica un parametro di scala t, il quale riscala la metrica sulla varietà quadrimensionale, e un parametro complesso u, relativo ai campi ausiliari che appaiono nell'integrale funzionale. Gli invarianti possono essere calcolati per ogni t; l'interpretazione degli invarianti tramite i moduli degli istantoni appare dal limite per t→0, dove l'attenzione si concentra nella regione data da u=0, e il campo ausiliario scompare. Nel caso dell'altro limite, t→∞, la situazione è descritta da una funzione analitica τ della variabile u (con alcune singolarità). Se b⁺₂(X)>1, si può mostrare che questa funzione τ è modulare rispetto all'azione di SL(2, Z). La parte essenziale di questa modularità è una simmetria u→u⁻¹ che corrisponde a una dualità tra elettricità e magnetismo proposta da D. Olive e C. Montonen nel 1977. Questa proprietà di modularità conduce alle funzioni ellittiche trovate da Fintushel e Stern nella loro formula per la somma connessa ed è così forte che la funzione τ è interamente determinata dalla sua espansione di Taylor intorno ai punti speciali u=±1.
La valutazione di questi coefficienti ha condotto agli invarianti di Seiberg-Witten; le argomentazioni di Seiberg e Witten prevedevano che la funzione generatrice degli invarianti degli istantoni di una varietà quadrimensionale X di tipo semplice (con b⁺₂(X)>1) potesse scriversi:
dove m(X)=2+(1/4) (7χ(X)+11σ(X)) (qui χ(X) è la caratteristica di Eulero e σ(X) è la segnatura di X) e
.
La finitezza di questa somma è la caratteristica delle equazioni di Seiberg-Witten le quali implicano due entità: una U(1)-connessione e un campo di spinori. Una SpinC-struttura è data da una coppia di C²-fibrati W± su X tali che la complessificazione del fibrato cotangente T*XC è uguale a (W⁺)*⊗W⁻. Le equazioni di Seiberg-Witten per una coppia (a,ϕ), dove a è una connessione abeliana sul fibrato di rette ∧²W⁺ e ϕ è una sezione di W⁺, sono
(con Da si indica l'operatore di Dirac). Usando la formula di Weitzenbock-Lichnerowich si può dimostrare che se una soluzione esiste allora si ottiene una maggiorazione superiore per c² (dove c=c₁(∧²W⁺)) e per un insieme finito di classi c in S₀⊂H²(X,Z). Una descrizione variazionale delle equazioni di Seiberg-Witten è data dal funzionale
dove E₀ dipende solo dalla curvatura scalare R della metrica su X:
.
Così le soluzioni di Seiberg-Witten sono minimi assoluti del funzionale E sul fibrato di rette proprio come gli istantoni di Yang-Mills minimizzano il funzionale ordinario di Yang-Mills. La linearizzazione di queste equazioni modulo il gauge abeliano è rappresentata da (d*+d⁺) che agisce sulle forme ordinarie e sull'operatore di Dirac; in tal modo la dimensione virtuale dello spazio delle soluzioni è
Da stime a priori sulle soluzioni si ottiene il successivo punto importante - la compattezza degli spazi di moduli di Seiberg-Witten MS₋W(c) (diversamente dal caso degli istantoni). I punti rimanenti sono la riducibilità e l'orientazione. La prima è esattamente come nel caso degli istantoni e la seconda è data da un'orientazione della retta dei determinanti ∧t°pH¹⊗∧t°pH⁺. Così c=c₁(∧²W⁺)∈S₀ implica dim MS₋W(c)=0 e la somma algebrica delle soluzioni fornisce un invariante numerico n(c). Le classi per le quali si ha n(c)≠0 vengono comunemente dette classi di Seiberg-Witten (brevemente classi SW). Witten ha mostrato che le classi di Seiberg-Witten di una superficie di Kähler sono componenti fisse di un sistema lineare canonico. Uno dei corollari di questo risultato è la soluzione finale di molte congetture fondamentali: la classe canonica del modello minimale di una superficie algebrica di tipo generale con pg>0 è, a meno del segno, un invariante differenziale. La dimensione di Kodaira di una superficie di Kähler è un invariante differenziale. Nella geometria simplettica tutte le varietà quadrimensionali condividono molte delle principali proprietà delle superfici di Kähler.
Una nuova caratteristica della tecnica di Seiberg-Witten è l'assenza dell'invarianza conforme per le equazioni relative, in contrasto con il caso Yang-Mills. Questo mostra che la classificazione delle varietà quadrimensionali con metriche a curvatura scalare positiva è radicalmente differente dal caso di dimensione superiore, nel quale la sola ostruzione proviene dalla teoria del cobordismo e dalle classi caratteristiche, a causa del teorema di annullamento per gli invarianti di Seiberg-Witten (relativamente alle varietà a curvatura scalare positiva). In particolare, una varietà tridimensionale a curvatura scalare positiva non può dividere una varietà quadrimensionale, con invarianti di Seiberg-Witten non banali, in modo che b⁺₂>0 valga per ognuno dei due lati. Un'altra applicazione di questa caratteristica della tecnica di Seiberg-Witten è stata data da Le Brun il quale ha mostrato che un'arbitraria varietà quadrimensionale di Einstein, con invarianti SW non nulli, soddisfa la disuguaglianza χ−3σ≥0. Per superfici complesse questo si riduce alla famosa disuguaglianza di Miyaoka-Yau c²₁≤3c₂.
bibliografia
C.N. Yang, R.L. Mills, Conservation of isotopic spin and isotopic gauge invariance, in Physical review, 1954, 96, pp. 191-95.
Y. Aharonov, D. Bohm, Significance of electromagnetic potentials in the quantum theory, in Physical review, 1959, 115, pp. 485-91.
P. Higgs, Spontaneous symmetry breakdown without massless bosons, in Physical review, 1966, 145, pp. 1156-63.
K.G. Wilson, Confinement of quarks, in Physical review, D, 1974, 10, pp. 2445-59.
M.F. Atiyah, Geometry of Yang-Mills fields, Pisa 1979.
L.D. Faddeev, A.A. Slavnov, Gauge fields - Introduction to the quantum field theory, Reading (Mass.) 1980.
A. Salam, Gauge unification of fundamental forces, in Review of modern physics, 1980, 92, pp. 525-36.
M.F. Atiyah, N.J. Hitchin, Geometry and dynamics of magnetic monopoles, Princeton 1988.
C. Taubes, A framework for Morse theory for the Yang-Mills functional, in Inventiones mathematicae, 1988, 94, pp. 327-402.
M.H. Freedman, F. Luo, Selected applications of geometry to low-dimensional topology, Providence (R.I.) 1989.
S. Donaldson, P. Kronheimer, The geometry of four-manifolds, Oxford 1990.
T. Petrie, J. Randall, Connections, definite forms and four-manifolds, Oxford 1990.
N. Seiberg, E. Witten, Monopoles, duality and chiral simmetry breaking in N=2 super-symmetric QCD, in Nuclear physics B, 1994, 431, pp. 581-640.
E. Witten, Monopoles and 4-manifolds, in Mathematical research letters, 1994, 1, pp. 764-96; J. W. Morgan, The Seiberg-Witten equations and applications to the topology of smooth four-manifolds, Princeton (N.J.) 1996.
Il teorema di Kolmogorov
di Vieri Mastropietro
Pubblicato nel 1954 in una nota di poche pagine, il teorema di Kolmogorov è uno dei risultati centrali della meccanica classica e della teoria dei sistemi dinamici. Esso ha risolto una serie di problemi che hanno impegnato per almeno due secoli alcuni fra i maggiori matematici e astronomi del passato e rivela oggi un'importanza sempre maggiore nell'ambito dell'analisi dei fenomeni non lineari.
Sistemi integrabili e non integrabili
L'ambito di tecniche e di problemi nel quale si colloca storicamente il lavoro di A.N. Kolmogorov è quello dell'astronomia matematica.
Nella meccanica classica il moto di ogni pianeta è determinato non solo dall'attrazione gravitazionale esercitata su di esso dal Sole, ma anche da quella esercitata da tutti gli altri pianeti. Il moto di un pianeta dipende quindi dalle posizioni istantanee di tutti gli altri e questo rende il calcolo dei moti planetari particolarmente complesso. Se però, in prima approssimazione, si immagina di trascurare l'interazione tra i pianeti, il problema si semplifica enormemente, poiché i pianeti divengono indipendenti gli uni dagli altri e occorre solo studiarne singolarmente il moto sotto l'azione di una forza centrale attrattiva. Questo problema è risolubile in modo elementare e si trova il ben noto risultato secondo il quale i pianeti si muovono rispettando le leggi di Keplero. Così in astronomia il moto del Sistema solare può venire descritto, nel suo complesso, dalla composizione di vari moti periodici: in questo caso si dice che il moto è quasi-periodico.
Il Sistema solare, nel caso in cui si consideri solo la forza gravitazionale tra i pianeti e il Sole, è un esempio di sistema integrabile. I sistemi di punti materiali soggetti solo a forze conservative vengono detti integrabili se è possibile trovare un sistema di coordinate (tramite un cambiamento di coordinate invertibile e non singolare) tale che: 1) tutte le configurazioni e velocità del sistema possono essere descritte in termini di l variabili di azione A→=A₁,…,Al ed l variabili angolari α→=α₁,…,αl; 2) il moto, descritto tramite queste coordinate, è tale che le variabili di azione restano costanti, mentre quelle angolari ruotano con velocità uniforme. In altre parole, le coordinate che descrivono il moto ruotano uniformemente su l circonferenze, e si può immaginare il sistema come un punto che si muove su un toro (in tre dimensioni un toro è una 'ciambella' su cui il moto può essere rappresentato tramite la composizione del moto su due circonferenze). In un sistema integrabile il moto avviene quindi su un toro invariante e la funzione hamiltoniana dipende solo dalle azioni, cioè essa è della forma H=H₀(A→).
Tuttavia, per ottenere previsioni astronomiche realmente migliori di quelle che si hanno applicando semplicemente le leggi di Keplero, occorre non trascurare l'interazione tra i pianeti. Poiché questa forza è immensamente più piccola di quella dovuta al Sole, appare ragionevole supporre (in prima approssimazione) che il suo effetto sia solo quello di 'perturbare', in modo quasi insensibile, il moto dei pianeti lungo le orbite kepleriane. Questo è certamente vero su intervalli di tempo piccoli, ma su tempi astronomici non vi è nessun motivo a priori per ritenere che le perturbazioni non debbano avere un effetto rilevante sul moto dei pianeti. In effetti è facile riscontrare deviazioni evidenti dalle leggi di Keplero se si dispone di dati astronomici su tempi sufficientemente lunghi. Sorge quindi la necessità di prevedere il moto dei pianeti in modo più preciso, e si pone al contempo il problema della stabilità del Sistema solare, ovvero di comprendere se l'influsso delle perturbazioni possa produrre o meno effetti catastrofici quali collisioni tra i pianeti o il loro indefinito allontanamento dal Sole. Il problema delle previsioni astronomiche e quello della stabilità del Sistema solare troverebbero soluzione, allo stesso tempo, se i pianeti si muovessero con moti quasi-periodici anche in presenza di perturbazioni. Questa fu la strada seguita dagli astronomi dell'Ottocento che cercarono soluzioni formali quasi-periodiche al problema planetario; tali soluzioni venivano espresse sotto forma di serie e le frequenze risultavano funzioni dell'entità della perturbazione.
L'hamiltoniana può essere scritta come H=H₀(A→)+εf(α→,A→), dove εf(α→,A→) è la perturbazione (per es. l'effetto dell'interazione tra i pianeti, nel caso considerato) ed ε il parametro perturbativo (per es. il rapporto tra la massa dei pianeti e quella del Sole). Si può procedere iterativamente cercando di trovare una trasformazione canonica che permetta di scrivere H=H(A→′)+ε²f(α→′,A→′): si avrebbe così un moto quasi-periodico, con frequenza dipendente da ε, a meno di correzioni di ordine ε². Poi si può cercare un'altra trasformazione che permetta di scrivere H=H₀(A→″)+ε³f(α→″,A→″) e così via. Tale procedura non è sempre possibile, perché queste trasformazioni sono affette dal problema dei 'piccoli divisori': questo significa che, nei denominatori dei coefficienti della trasformazione, compaiono dei fattori ω→ν→ (dove ν→∈Zl) i quali possono annullarsi se le frequenze sono commensurabili. In generale questi fattori possono divenire arbitrariamente piccoli. I valori di ω→ per cui esistono degli interi tali che ω→ν→=0 vengono detti risonanze. Se si riesce a iterare questa procedura infinite volte, si trova che tutti i moti sono quasi-periodici e le frequenze risultano espresse in termini di serie formali.
Queste serie formali non sono tuttavia in generale convergenti. Se lo fossero, tutti i sistemi dovrebbero essere integrabili; ma questo è falso, come venne mostrato da H. Poincaré con la sua famosa dimostrazione della non integrabilità del problema dei tre corpi: "Queste serie non sono in grado di raggiungere una precisione indefinitamente accurata" scrisse Poincaré, "è per questo che non possono servire a risolvere la questione della stabilità del sistema solare" (Poincaré 1899). Tale risultato negativo sembra suggerire che non esistano moti planetari quasi-periodici in presenza di perturbazioni e pone dei limiti alla capacità di prevedere il moto dei pianeti su tempi lunghi. La concezione meccanicistica dell'universo, immaginato come una sorta di orologio in cui i pianeti si muovono come le lancette di un quadrante, viene in qualche modo incrinata da questi risultati.
Poincaré vinse il premio messo in palio dal re di Svezia per colui che avesse dimostrato l'esistenza di moti quasi-periodici in un problema planetario 'realistico', mostrando come i suoi risultati indicassero la non esistenza di tali moti. In verità, come venne osservato da K. Weierstrass, i risultati di Poincaré non erano evidentemente conclusivi, in quanto provavano solo che non tutti i moti erano quasi-periodici in presenza di perturbazioni. Era ancora possibile che, per opportune condizioni iniziali, alcuni moti fossero quasi-periodici anche in presenza di perturbazioni. Poincaré affrontò anche tale questione e ottenne soluzioni quasi-periodiche con frequenza fissata; tali soluzioni erano espresse tramite serie formali. Pur non essendo in grado di escludere la convergenza di queste serie, dette serie di Lindstedt, egli osservò che la loro convergenza "era molto inverosimile".
In sostanza questa era la situazione prima del lavoro di Kolmogorov: in presenza di perturbazioni, era impossibile che tutti i moti fossero ancora quasi-periodici (poiché le serie perturbative che li esprimevano erano divergenti) e appariva inoltre assai improbabile che alcuni di tali moti permanessero; non esistevano algoritmi in grado di prevedere la posizione dei pianeti per tempi arbitrariamente lunghi; non era possibile fare alcuna previsione di lungo periodo sul comportamento di sistemi meccanici ottenuti perturbando sistemi integrabili. In generale, pareva impossibile che il Sistema solare, anche in assenza di forze esterne, fosse eternamente stabile.
Il lavoro di Kolmogorov
Nel 1954, contrariamente a queste osservazioni, Kolmogorov ha dimostrato che, sotto certe condizioni, perturbando debolmente un sistema integrabile si ottiene un sistema che, per gran parte dei dati iniziali, si muove essenzialmente allo stesso modo del precedente ovvero in modo quasi-periodico (Kolmogorov 1954). Memore dei risultati di Poincaré, Kolmogorov non tenta di dimostrare che tutti i moti del sistema perturbato sono quasi-periodici. Al contrario cerca dei moti con frequenza fissata, in particolare moti quasi-periodici in cui la frequenza, in presenza o meno di perturbazioni, sia la stessa; inoltre egli considera solo frequenze che verificano una condizione diofantina, ovvero una condizione di forte incommensurabilità tra le frequenze. Questa richiesta serve a controllare il problema dei piccoli divisori. Il fatto di fissare le frequenze dei moti, e di non scriverle come funzioni della perturbazione, è una differenza fondamentale rispetto all'approccio classico. Questo è il contenuto del suo teorema: una hamiltoniana della forma H₀(A→)+εf(α→, A→), analitica in A→ in una regione S dello spazio euclideo l-dimensionale e in α→ sul toro l-dimensionale Tl, ammette una famiglia di moti quasi-periodici (che iniziano ad α→=0) della forma A→(t)=A→₀+εH→(A→₀,ω→₀ t;ε), α→(t)=ω→₀t+εh→(A→₀,ω→₀ t;ε), dove ω→₀=ω→(A→₀), purché ε sia sufficientemente piccolo, si abbia det(∙Ai ∙Aj H₀(A→₀))≠0 e ω→₀ verifichi una condizione diofantina, ovvero esistano C₀, τ tali che C₀|ω→₀ν→|≥|ν→|⁻τ per ogni ν→≠0→, ν→∈Zl. Inoltre H(A→,ψ→;ε) e h→(A→,ψ→;ε) sono funzioni analitiche in A→∈S, in ψ→∈Tl e in ε, per ε sufficientemente piccolo; h (A→,ψ→;ε) ha media nulla in Tl.
Poiché le frequenze dipendono dai dati iniziali, restringersi a frequenze diofantine significa che solo una parte dei dati iniziali conduce a moti quasi-periodici; tuttavia, scelto a caso un dato iniziale, vi è un'alta probabilità che esso conduca a un moto quasi-periodico, anche in presenza di perturbazione; questa probabilità è tanto più grande quanto minore è l'entità della perturbazione. Più precisamente, la misura di Lebesgue dei dati iniziali che non evolvono in modo quasi-periodico è piccola e tende a zero per ε che tende a zero. Il fatto che di tale insieme si sappia solo che è piccolo, nel senso della misura di Lebesgue, implica che tale insieme di dati iniziali può essere anche molto complesso: in pratica può essere molto difficile decidere se un certo dato evolve o no in modo quasi-periodico.
Pur essendo migliorabili, le condizioni poste da Kolmogorov per l'esistenza di soluzioni quasi-periodiche sono in gran parte ineliminabili. Se non sono verificate, i moti quasi-periodici spesso non esistono, come può essere oggi confermato tramite simulazioni numeriche al calcolatore. In generale, per certi valori delle masse dei pianeti e delle loro posizioni e velocità iniziali, è possibile che i moti planetari siano caotici e di conseguenza non prevedibili su tempi lunghi (v. caos e complessità, App. V). È facile quindi immaginare esempi di sistemi planetari i cui abitanti non nutrano la fiducia che abbiamo noi nella regolarità e armonia dei moti celesti e non contrappongano, così nettamente, i moti celesti a quelli terrestri. Del resto, nel nostro stesso Sistema solare, si scoprono sempre più spesso esempi di moti caotici, come quelli proposti da J. Laskar e P. Robutel (1993).
Anche se le condizioni di Kolmogorov non sono verificate, potrebbero ugualmente esistere moti quasi-periodici, ma con frequenza diversa rispetto al caso non perturbato. Per es. se la condizione det(∙Ai∙AjH₀(A→₀))≠0 non è verificata (come nel caso H₀=ω→A→ ed f(α→,A→)=A→) i moti sono ancora quasi-periodici per ogni ε, ma avvengono tutti con frequenza (1+ε)ω→ e non ω→.
Abbiamo inoltre visto che è utile rappresentare il moto di un sistema integrabile come moto quasi-periodico su un toro invariante; se si considera una perturbazione e si assumono le condizioni di Kolmogorov, la maggior parte di questi tori non sparisce, ma subisce una piccola deformazione e il moto avviene con frequenze che sono le stesse del sistema non perturbato. Come a volte avviene, il contributo di Kolmogorov, è consistito più nell'intuizione di cosa esattamente dimostrare che nelle tecniche usate. Infatti egli ha preferito evitare gli sviluppi in serie di potenze tipici dei precedenti metodi, e ha usato uno sviluppo rapidamente convergente, il quale dopo n approssimazioni dà un errore di ordine non εn ma ε²n; questo effetto di 'superconvergenza' riesce a compensare l'effetto dei piccoli divisori e, in tal modo, si può dimostrare la convergenza del metodo. Come si vedrà in seguito, le stesse serie di Lindstedt scritte da Poincaré (serie apparentemente non convergenti) sono, sotto le ipotesi di Kolmogorov, convergenti e possono essere usate per dare una nuova dimostrazione del teorema. Il teorema di Kolmogorov ricevette una sorta di conferma sperimentale dal contemporaneo lavoro di E. Fermi, J. Pasta e S.M. Ulam, i quali studiarono numericamente un sistema di oscillatori perturbato. Essi si aspettavano di trovare dei moti caotici, ma al contrario trovarono moti piuttosto stabili: tale comportamento poteva essere interpretato alla luce del teorema di Kolmogorov.
Il teorema KAM
di Vieri Mastropietro
Nel 1963 V.I. Arnol´d (allievo di Kolmogorov) ha riderivato il teorema utilizzando un metodo diverso (Arnold 1963a). Egli era motivato dall'estrema mancanza di dettagli del lavoro di Kolmogorov. Ancor più importante è stato il contributo di Arnol´d nel mostrare come tale teorema possa essere esteso al punto da essere applicabile alla dinamica del Sistema solare (Arnold 1963b). Infatti, nel caso del Sistema solare le frequenze non verificano una condizione diofantina (i singoli pianeti si muovono di moto periodico, non quasi-periodico, e quindi le loro frequenze non sono indipendenti); operando però sulla hamiltoniana opportune trasformazioni canoniche e quindi applicando il teorema di Kolmogorov, è possibile mostrare che i moti dei pianeti, per la maggior parte dei dati iniziali, sono effettivamente stabili rispetto a piccole perturbazioni. Dunque il problema della stabilità può dirsi, almeno concettualmente, risolto: anche tenendo conto dell'attrazione tra i pianeti, un sistema solare può avere moti quasi-periodici e quindi essere stabile. Resta aperto il problema se il nostro Sistema solare, con le masse e le velocità sperimentalmente misurate, rientri o meno nelle condizioni di validità di questo teorema.
Un'altra profonda estensione del teorema di Kolmogorov è dovuta a J. Moser che ha mostrato nel 1962 come l'ipotesi di analiticità nelle azioni e negli angoli per la hamiltoniana possa essere rilassata e sostituita con quella di derivabilità. In particolare si richiede che H appartenga a Cn, con n>2τ+2 (Moser 1962). Tale dimostrazione usa ancora un'espansione superconvergente in combinazione con un processo di mollificazione analogo a quello introdotto da J. Nash (1956). Il risultato è particolarmente sorprendente e inaspettato. Bisogna sottolineare che, a differenza del risultato di Kolmogorov, questo risultato non sembra essere derivabile dalle serie di Lindstedt. Il corpus dei risultati ottenuti da questi tre matematici è oggi noto col nome di teorema KAM, dove l'acronimo deriva dalle loro iniziali.
Una nuova dimostrazione del teorema di Kolmogorov è stata fornita da L.H. Eliasson nel 1988, considerando le serie di Lindstedt scritte da Poincaré e mostrando la loro convergenza sotto le assunzioni fatte da Kolmogorov. È stato quindi necessario attendere più di un secolo perché il problema della convergenza delle serie di Lindstedt, posto da Poincaré, venisse risolto. Eliasson ha mostrato che i piccoli divisori producono nella serie (all'ordine n) coefficienti di ordine n!α, dove α è una costante positiva opportuna; questi contributi 'grandi' si compensano l'uno con l'altro grazie a opportune cancellazioni (Eliasson 1988). Successive derivazioni di questo risultato hanno evidenziato come la tecnica qui applicata sia sorprendentemente simile ad altre tecniche usate nella teoria dei campi quantistici o in meccanica statistica per dimostrare la convergenza di serie perturbative di determinate grandezze fisiche (Gallavotti 1994).
Applicazioni
Il teorema di Kolmogorov mostra come sia possibile fare previsioni sul moto dei pianeti, valutando gli errori delle approssimazioni fatte, per tempi arbitrari. La teoria perturbativa, dapprima guardata con sospetto dopo le dimostrazioni di non convergenza date da Poincaré, C. L. Siegel e altri, si conferma invece uno strumento potente e affidabile. In pratica, per ottenere dimostrazioni di stabilità per i moti di corpi celesti è necessario ottimizzare le stime del teorema di Kolmogorov; non è sempre chiaro se un dato moto rientri o meno nelle condizioni di applicabilità del teorema. Di conseguenza, alla fine del 20° sec. è ancora ignoto se i moti dei pianeti del nostro Sistema solare siano o meno stabili, e anzi alcuni importanti astronomi come Laskar ritengono che il moto del Sistema solare sia caotico, anche se dei fenomeni di instabilità dovrebbero apparire su scale di tempo dell'ordine di grandezza della vita del Sistema solare stesso (Laskar, Robutel 1993). Comunque, utilizzando tecniche KAM sono state ottenute delle stime di stabilità per vari corpi celesti, asteroidi o satelliti (Celletti 1993).
Non sorprende l'importanza del teorema di Kolmogorov anche in applicazioni tecnologiche, come la previsione del moto dei satelliti artificiali o la progettazione di acceleratori di particelle. Il teorema di Kolmogorov mostra infatti con quali dati iniziali i moti restano stabili anche per tempi lunghissimi sotto l'effetto di perturbazioni (le quali sono presenti in qualsiasi sistema) e quindi ha importanza per la progettazione di sistemi complessi. Infine il teorema di Kolmogorov ha trovato applicazioni anche in ambiti molto lontani rispetto a quelli in cui è nato. Per es. la presenza, in alcuni metalli fortemente anisotropi, di onde di densità di carica con un periodo incommensurabile rispetto al reticolo cristallino ha stimolato il sorgere di una serie di studi matematici, dovuti a S. Aubry, Y.G. Sinai, Moser, L. Pastur, Eliasson e altri, dedicati alla soluzione dell'equazione di Schrödinger con un potenziale quasi-periodico (Pastur, Figotin 1991). Lo studio di tali soluzioni viene portato avanti utilizzando i metodi del teorema KAM; in questo filone si inserisce un risultato di Aubry e P.Y. Le Daeron (1983) in cui, utilizzando modelli semplificati, si spiega la presenza di queste onde di carica con il teorema di Kolmogorov.
Sviluppi recenti
La ricerca più recente si è concentrata sullo studio dei moti di sistemi perturbati nei casi in cui le condizioni di validità del teorema di Kolmogorov vengano meno. È questo un campo di ricerca vastissimo e in tumultuosa evoluzione: qui si può solo accennare ad alcuni dei risultati più importanti.
Se non si considerano, come nel teorema di Kolmogorov, perturbazioni di moti con frequenze fortemente incommensurabili, ma al contrario si considerano frequenze commensurabili (risonanze), si ha che una perturbazione comunque piccola può modificare radicalmente la natura del moto: infatti non è restrittivo supporre che, in corrispondenza di una risonanza, alcune frequenze siano nulle (tramite un cambio di variabili ci si può sempre ridurre a questo caso) e quindi il moto sia interamente determinato dalla perturbazione. In generale tendono ad apparire moti caotici, ma anche altri tipi di moti, come quelli quasi-periodici con periodo non connesso a quello non perturbato. Si può mostrare, per es., che in prossimità di una risonanza il moto in presenza di perturbazioni somiglia, se i gradi di libertà sono due, a quello di un pendolo forzato; il meccanismo con cui si producono moti caotici è quello dei 'punti omoclinici' (Moser 1973).
Una perturbazione per cui valgano le ipotesi del teorema di Kolmogorov modifica ben poco la variabile di azione rispetto al suo valore iniziale. Invece, nel caso in cui la perturbazione non soddisfi tali condizioni, la variabile di azione potrebbe cambiare in modo rilevante. N. Nekhorossiev ha mostrato come questo, in molti casi, debba avvenire in tempi piuttosto lunghi: in particolare in corrispondenza di una risonanza se
è definita positiva, per tempi anche dell'ordine di eB/εb, le azioni A→(t) cambiano, rispetto al loro valore all'istante iniziale, al più di una quantità proporzionale a εa, dove B, a, b sono costanti positive opportune (Nekhorossiev 1975). In generale la situazione è comunque assai diversa quando si passa da sistemi con due gradi di libertà a sistemi con tre o più gradi di libertà. Nel primo caso la variabile d'azione non può allontanarsi rispetto al suo valore iniziale di più di −ε. Questo è dovuto a un motivo essenzialmente geometrico: se il sistema ha due gradi di libertà e l'energia si conserva, il moto può essere visualizzato come il moto di un punto in uno spazio tridimensionale. In tal caso i tori invarianti previsti dal teorema di Kolmogorov sono delle superfici che dividono lo spazio in regioni distinte e che non possono essere attraversate (altrimenti verrebbe violato il teorema di unicità delle equazioni differenziali); a causa di ciò i punti non possono allontanarsi troppo dal loro valore iniziale. Invece, se il sistema ha più di due gradi di libertà, questo non avviene, poiché i tori invarianti non dividono lo spazio in regioni distinte.
Arnol´d (1966) ha fornito un esempio in cui si mostra come, in un certo sistema perturbato, le coordinate di azione possano variare di una quantità indipendente da ε pur di aspettare un tempo abbastanza lungo. Questo fenomeno viene detto diffusione di Arnol´d e può essere di estrema importanza, perché mostra come perturbazioni arbitrariamente piccole, apparentemente trascurabili, possano avere conseguenze rilevanti sul moto di un sistema. Si suppone che un fenomeno di questo tipo sia responsabile della variazione, su scala di tempo del milione di anni, dell'asse di rotazione dei pianeti maggiori di addirittura 60°. Un grosso sforzo viene attualmente compiuto per mostrare come la diffusione di Arnol´d sia un meccanismo generico che si può riscontrare in modelli diversi di interesse fisico (Chierchia, Gallavotti 1994). Tale programma si scontra con le varie assunzioni semplificanti che sono nascoste nel modello studiato da Arnol´d: infatti, egli considera perturbazioni di moti con punti fissi iperbolici, mentre nelle applicazioni si è interessati a trovare diffusioni in perturbazioni di moti quasi periodici; inoltre, la perturbazione è di una forma molto speciale e così via. Nonostante ciò in tale settore sono stati realizzati notevoli progressi.
Un altro problema interessante è quello di esaminare cosa avvenga ai tori invarianti eliminando l'ipotesi di piccolezza della perturbazione. Da simulazioni numeriche al calcolatore si vede che questi tori gradualmente spariscono e che il valore di ε per cui questo avviene è legato al grado di irrazionalità della frequenza. Nel caso di sistemi con due gradi di libertà e con tempi discreti è stato scoperto che gli insiemi invarianti previsti dal teorema KAM lasciano il posto, all'aumentare della perturbazione, a insiemi invarianti che non sono più delle curve regolari bensì insiemi assai complessi. Questo è stato mostrato invertendo l'approccio di Kolmogorov e scambiando il ruolo della hamiltoniana non perturbata e della perturbazione, ovvero considerando H₀(A→) piccola rispetto a εf(α→, A→) e usando il teorema delle funzioni implicite. Tali insiemi sono chiamati cantori, per distinguerli dai tori del teorema KAM e per ricordare che sono degli insiemi di Cantor. Essi sono stati scoperti indipendentemente da Aubry, studiando metalli fortemente anisotropi, e da Mather, considerando sistemi dinamici a tempi discreti (Mather 1982; Aubry 1983). Infine altri sviluppi importanti riguardano la comprensione di risultati simili a quello di Kolmogorov nel caso di sistemi con un numero infinito di gradi di libertà o nel caso di sistemi che obbediscono alle leggi della meccanica quantistica.
bibliografia
H. Poincaré, Les méthodes nouvelles de la mécanique céleste, Paris 1899.
A.N. Kolmogorov, On the preservation of conditionally periodic motions, in Doklady akademii nauk SSSR, 1954, 96, pp. 527-30.
J. Nash, The embedding of riemannian manifolds, in Annals of mathematics, 1956, pp. 20-63.
J. Moser, On invariant curves of an area preserving mapping of the annulus, in Nachrichten der Akademie der Wissenschaften in Göttingen, 1962, pp. 1-20.
V. Arnold, Proof of a theorem of A.N. Kolmogorov on the invariance of quasi-periodic motions under small perturbations of the hamiltonian, in Russian mathematical surveys, 1963a, 5, pp. 9-36.
V. Arnold, Small denominators and the problems of stability of motion in classical and celestial mechanics, in Russian mathematical surveys, 1963b, 6, pp. 85-191.
E. Fermi, Collected papers of E. Fermi, Chicago 1965.
V. Arnold, Instability of dynamical systems with several degrees of freedom, in Sovetskie matematičeskie doklady, 1966, 5, pp. 581-85.
J. Moser, Stable and random motions in dynamical Systems, with special emphasys on celestial mechanics, Princeton 1973.
N. Nekhorossiev, An exponential estimate of the time of stability of nearly integrable hamiltonian systems, in Russian mathematical surveys, 1975, pp. 1-65.
G. Casati, J. Ford, Stochastic behaviour in classical and quantum hamiltonian, Berlin 1979.
J.N. Mather, Existence of quasi-periodic orbits for twist homeomorphism of the annulus, in Topology, 1982, pp. 457-67.
S. Aubry, P.Y. Le Daeron, The discrete Frenkel-Kontorova model and its extensions I, in Physica D, 1983, 8, pp. 381-422.
L.H. Eliasson, Absolutely convergent series expansion for quasi-periodic motions, in Report 2, Department of Mathematics, University of Stockholm, 1988.
L. Pastur, A. Figotin, Spectra of random and almost periodic operators, Berlin 1991.
A. Celletti, Construction of librational invariant tori in the spin orbit problem, in Journal of applied mathematics and physics, 1993, pp. 61-80.
J. Laskar, P. Robutel, The chaotic obliquity of the planets, in Nature, 1993, 361, pp. 608-12.
L. Chierchia, G. Gallavotti, Drift and diffusion in phase space, in Annales de l'Institut Poincaré, 1994, 60B, pp. 1-144.
G. Gallavotti, Twistless KAM tori, in Communications in mathematical physics, 1994, 164, pp. 145-96.