Logiche non standard

Logiche non standard

Alcune famiglie di logiche non standard sono costituite da logiche che sono estensioni assiomatiche di quella standard, mentre altre constano di logiche rappresentabili come indebolimenti di questa. Alla prima classe appartengono le logiche modali, volte ad assiomatizzare le nozioni interdefinibili con quella di possibilità e inizialmente studiate con particolare attenzione alla nozione di implicazione stretta (cioè necessaria). Dopo che Kurt Gödel ebbe mostrato l'insostenibilità dell'interpretazione dell'implicazione stretta in termini di deducibilità formale, solo negli anni Sessanta del Novecento è stata conseguita un'analisi semantica dei principali sistemi modali, di cui è stato possibile dimostrare la completezza e la decidibilità. L'idea chiave della semantica cosiddetta relazionale è che la verità di una proposizione necessaria in un dato mondo w equivale alla verità di tale proposizione in una classe di mondi che sono possibili in relazione a w. I sistemi modali detti normali si distinguono semanticamente per le diverse proprietà godute dalla relazione in oggetto, detta di accessibilità. Di fatto essi sono solo alcuni degli svariati sistemi classificabili come modali o intensionali: si dànno infatti linguaggi con operatori modali metrici, con operatori modali a due o più posti (come i condizionali di Stalnaker-Lewis) e con operatori definibili via costanti proposizionali. Più recentemente sono diventati di uso comune linguaggi multimodali, cioè con più di un operatore modale primitivo.

Alla famiglia delle logiche multimodali appartengono tra l'altro le varie logiche del tempo (in cui gli assiomi contengono operatori per il passato e per il futuro) e varie versioni delle logiche del conoscere e del credere (logiche epistemiche), in cui gli operatori sono indicizzati dai soggetti epistemici. L'estensione del linguaggio modale con quantificatori e identità introduce una classe di problemi non formulabili a livello proposizionale, come quello della distinzione de dicto/de re e dell'identificazione attraverso mondi possibili. È stato peraltro provato che nella logica modale quantificata ci sono infiniti sistemi modali incompleti rispetto alla semantica relazionale, aprendo così il problema di una riconsiderazione di questa.

Venendo alle logiche più deboli della standard, un posto di rilievo è occupato dalle logiche (intuizioniste o costruttive) prive della legge del terzo escluso. La possibilità di rappresentare tali sistemi entro sistemi modali forti ha aperto la strada a una diversa nozione di mondo possibile, trattabile come un insieme più o meno incompleto di informazioni. Le logiche dette sottostrutturali invece indeboliscono o eliminano alcune regole inferenziali che non coinvolgono i connettivi classici. A questa classe appartengono le principali logiche della rilevanza e dell'entailment, in cui si mira a escludere qualsiasi regola che, consentendo di aggiungere antecedenti arbitrari, impedisca di rappresentare l'implicazione come risultato di un impiego effettivo dell'antecedente nella derivazione del conseguente. Tra le molte logiche implicative reperibili nella letteratura compaiono logiche (dette connessive) contenenti una tesi ‒ asserente che niente può implicare la propria negazione ‒ che è incompatibile con la logica standard. Risulta dunque che ci sono famiglie di logiche i cui elementi possono non risultare classificabili né come estensioni né come sottosistemi della logica standard. Altri esempi sono offerti dalla famiglia delle logiche modali ottenibili per estensione assiomatica della logica intuizionista o delle logiche quantificate per termini non denotanti (logiche libere). L'inconfrontabilità con la logica standard dipende spesso dall'adozione di linguaggi inconfrontabili con quello classico. Logiche di questo tipo si incontrano nella classe delle logiche polivalenti, quantistiche, lineari, paraconsistenti e dialettiche.

In queste logiche la presenza nel linguaggio di operatori non classici rispecchia la divergenza della loro semantica basata su tavole di verità a più valori, rispetto alla semantica standard, che è rigidamente bivalente e conserva questa caratteristica anche nelle sue estensioni modali. Nelle logiche sfumate (fuzzy) la divergenza con la logica standard è più radicale perché importa la vaghezza del linguaggio ordinario a livello delle stesse nozioni insiemistiche e dei connettivi che le rappresentano.

Va aggiunto che altre famiglie di logiche risultano inconfrontabili con quella standard non tanto per la sintassi, ma per l'impiego di nozioni metasistematiche non-classiche, come le logiche non-monotòne, le logiche per il default reasoning e le varie logiche volte a cogliere formalmente il ragionamento induttivo e abduttivo.

Logiche più forti della logica standard

L'idea di usare la logica standard come base a cui aggiungere assiomi o regole descriventi le proprietà di concetti specifici fa parte della tradizione logica del XX sec., come si desume ‒ per fare due soli esempi ‒ dalla teoria assiomatica degli insiemi di Ernst Zermelo (1908) e dalla logica induttiva di Rudolf Carnap (1950). Tali assiomatizzazioni avevano però per oggetto nozioni considerate extralogiche, mentre le nozioni modali fondamentali (necessario, possibile, impossibile, contingente), a cui Aristotele dedicava nell'Organon una parte importante della sillogistica, a fine Ottocento venivano per lo più considerate nozioni parafrasabili nel linguaggio o nel metalinguaggio della logica standard ‒ per esempio identificando 'necessario' con 'analitico' o 'logicamente valido' ‒ e quindi non meritevoli di trattazione indipendente. Questo riduzionismo, rappresentato nel XX sec. soprattutto dalla filosofia di Willard Van Orman Quine, a parte le diverse difficoltà teoriche in cui incorre, appare oggi anacronistico in quanto la logica modale ha raggiunto una posizione centrale nel panorama logico proprio emancipandosi dalla logica standard.

Anche se non mancavano spunti interessanti già nell'Ottocento (Hugh MacCall), la rifondazione della logica modale è stata compiuta da Clarence I. Lewis e Cooper H. Langford in Symbolic logic (1932). Il problema da cui partivano i due autori era l'insufficiente trattazione dell'implicazione riscontrabile nella logica standard. Il condizionale materiale, che Bertrand Russell e Alfred N. Whitehead simbolizzavano come A⊃B, equivale alla disgiunzione ∉A B, e quindi è vero quando A è falso o B è vero. Il senso implicativo di A⊃B in realtà emerge solo quando A⊃B è un teorema della logica di riferimento, nel qual caso si può applicare la regola del modus ponens che consente di inferire la conclusione B dall'ipotesi A. Ma dire che A⊃B è un teorema o una tautologia di una logica determinata significa fare un asserto su A⊃B, e quindi porsi a livello metalinguistico rispetto al condizionale materiale. Per evitare questa confusione di livelli veniva proposto di affiancare al condizionale simbolizzato da ⊃ un condizionale rappresentante l'implicazione in senso stretto (strict implication), simbolizzata da a e governata da appositi assiomi. Se  è il simbolo per la nozione di possibilità, si possono anche introdurre assiomi minimali per  e definire poi il simbolo a mediante AaB=_Def ∉(A ∉B). Alternativamente, introducendo il simbolo □ per la nozione di necessità, si può usare la definizione AaB=_Def □(A⊃B) per esprimere l'idea che A implica strettamente B se e solo se A⊃B è necessariamente vera. Assumendo l'equivalenza delle due definizioni si ottiene ∉(A ∉B)≡□(A⊃B) e, ponendo al posto di A un'arbitraria tautologia T, si ottiene ∉∉B≡□B e quindi, con banali passaggi, B≡∉□∉B. Possibilità e necessità risultano quindi nozioni duali tra loro e manifestano una relazione analoga a quella che intercorre tra quantificatore universale e quantificatore esistenziale.

Lewis e Langford non erano però tassativi circa le proprietà logiche delle nozioni simbolizzate da □, , a. Introducevano infatti non uno ma cinque sistemi di implicazione stretta, da S1 a S5. I due sistemi S4 e S5 evidenziano seri motivi di incertezza che riguardano le cosiddette modalità iterate. L'assioma caratteristico di S4 è 4: □A≡□□A, mentre l'assioma di S5 è 5: A≡□A. Ci sono interpretazioni di □ che non consentono di accettare nessuno dei due, mentre altre rendono intuizioni plausibili il primo ma non il secondo.

È degno di nota che nella proposta di cinque sistemi modali venisse abbandonato il monismo logico, cioè il presupposto per cui c'è un unico modo privilegiato per assiomatizzare una famiglia di concetti data. Per quanto riguarda le modalità, si apriva la strada all'idea che, fatti salvi alcuni presupposti minimali, c'è uno spettro ampio o addirittura infinito di assiomi atti a descrivere le nozioni modali o, alternativamente, che ci sono infinite nozioni modali simili dotate di proprietà descrivibili assiomaticamente.

Gli autori erano comunque sostanzialmente fedeli all'approccio sintattico e in particolare all'idea secondo cui qualche insieme prefissato di assiomi e regole sia sufficiente a caratterizzare il significato delle nozioni modali. Ma un breve articolo di Gödel (1933) scoraggiava questa prospettiva. Supponiamo di identificare 'necessario' con 'dimostrabile nell'arimetica' e quindi 'possibile' con 'consistente con l'aritmetica'. Conveniamo di chiamare KT il sistema ottenuto aggiungendo al calcolo proposizionale standard gli assiomi K: □(A⊃B)⊃(□A⊃□B) e T: □A⊃A nonché la cosiddetta regola di necessitazione forte ⊦A→⊦□A. Assumendo KT e adottando il linguaggio dell'aritmetica si otterrebbe come teorema ∉(0≠0)⊃∉(0≠0) e quindi, facendo uso del modus ponens, ∉(0≠0). Ma questo equivarrebbe a dire che in un sistema contenente l'aritmetica è dimostrabile la consistenza dell'aritmetica, il che è impossibile per un ben noto corollario del teorema di Gödel.

Pochi anni dopo (1940) un teorema dimostrato da James Dugundji, evidenziando il carattere non-verofunzionale degli operatori modali, dimostrava che nessuna logica modale può avere una matrice caratteristica finita. Se il risultato di Gödel gettava un'ombra sulla trattazione sintattica della logica modale, il teorema di Dugundji suscitava perplessità sulla sua semantica, suggeriva (erroneamente) l'idea che fosse impossibile determinare una procedura di decisione per le logiche modali fondamentali e faceva anche ritenere problematica una loro analisi semantica.

Lewis e Langford non offrivano un'interpretazione semantica delle modalità, pur sapendo che una semplice chiave interpretativa era già stata suggerita da Gottfried Wilhelm Leibniz nel Settecento: sono necessarie quelle proposizioni che sono vere comunque vada il mondo, e cioè vere in tutti i mondi possibili. Ispirandosi a questa idea base, Carnap provava nel 1947 che il sistema S5 risulta decidibile e completo rispetto a una semantica in cui la necessità viene interpretata leibnizianamente. Mancava una caratterizzazione semantica dei sistemi più deboli di S5, ma nel giro di pochi anni la via per la soluzione del problema veniva indicata da Jaakko Hintikka, Stig Kanger e Richard M. Montague. Nel 1959 Saul Kripke dimostrava un risultato di completezza e decidibilità per i tre sistemi modali più forti: KT, S4, S5. L'idea su cui si regge la nuova semantica ‒ detta semantica di Kripke o semantica relazionale ‒ è quella di intendere la necessità come verità in una sottoclasse della classe di tutti i mondi possibili, costituita da mondi che hanno una relazione R ‒ detta di accessibilità ‒ con il mondo w° rispetto a cui vengono valutate le formule. □A si dirà quindi vera a w° se e solo se A è vera in tutti i mondi w_j tali che w°Rw_j. Proprietà diverse di R caratterizzano sistemi diversi. Le tesi di KT risultano KT-valide, ossia vere in tutti i mondi di tutti i KT-modelli, definiti come triple 〈W,R,V〉 in cui W è un insieme non vuoto di mondi, R una relazione riflessiva su W, V è una funzione che associa a coppie di proposizioni e mondi un valore nell'insieme {1,0}. Negli S4-modelli la R è riflessiva e transitiva, negli S5-modelli una relazione di equivalenza. I risultati di completezza dimostrati da Kripke assicurano che tutte e sole le KT(S4,S5)-tesi sono valide nelle classi di modelli correlati.

Ma la completezza di un sistema può essere dimostrata rispetto a classi diverse di modelli: per esempio S5 è completo anche rispetto alla classe dei modelli in cui R intercorre tra tutti i mondi possibili, mentre K, ottenuto eliminando dalla logica KT l'assioma T, è completo rispetto alla classe di tutti i modelli e anche di tutti i modelli irriflessivi. Inoltre, dato che i sistemi più studiati presentano assiomi che risultano casi speciali dello schema

[1] ^m□ⁿA ╔ □ ^j^kA m, n, j, k≥0

si può dimostrare un teorema di completezza generalizzato rispetto a classi di modelli in cui le proprietà di R rientrano nello schema

[2] ∀w₁, w₂, w₃, w₄

((w₁R^mw₂ w₁R^jw₃)⊃∃w₄(w₂Rⁿw₄ w₃R^kw₄))

dove m,j,n,k≥0 indicano in [1] il numero di operatori modali iterati e in [2] il numero di passi della relazione R (ponendo w₁R⁰w_k uguale a w_i=w_k). Per esempio l'assioma 4 (p⊃p) è il caso speciale di [1] in cui m=0, n=1, j=2, k=0, mentre i modelli che lo convalidano sono tali che se si passa da w₁ a w₄ in due passi allora si passa da w₁ a w₄ in un solo passo (cioè la relazione R è transitiva).

La cosiddetta teoria della corrispondenza (sviluppata da Johan Van Benthem negli anni Settanta) studia il rapporto tra le formule modali e le formule classiche che descrivono le proprietà dei modelli relazionali. Se in un modello 〈W,R,V〉 isoliamo la parte strutturale 〈W,R〉 (detta frame o struttura), è abbastanza intuitivo, per cominciare, che non tutte le proprietà relazionali delle strutture sono esprimibili da formule modali: non lo sono per esempio l'irriflessività, l'intransitività e l'asimmetria. Se la verità in una struttura è la verità in tutti i modelli su quella struttura, tra i vari risultati della teoria si ha: (a) che non tutti i sistemi sono completi rispetto a qualche classe di strutture e (b) che non tutti gli assiomi modali sono convalidati da modelli in cui la R ha proprietà esprimibili al primo ordine. Due esempi: la logica K+□(□p≡p)⊃□p non è convalidata da nessuna classe di strutture ed è quindi incompleta rispetto a strutture (anche se completa rispetto a qualche classe di modelli); la logica K+□p⊃□p risulta invece completa rispetto a tutte le strutture che sono riflessive, transitive e dotate di almeno un punto terminale, ma questa proprietà è definibile solo al secondo ordine.

Le logiche in cui □ è interpretato come 'è dimostrabile nell'aritmetica' sono caratterizzate dal cosiddetto assioma di Löb: □(□p⊃p)⊃□p e sono complete rispetto a modelli in cui R è transitiva e ha una conversa ben fondata (cioè non esiste nessuna sequenza infinita ordinata da essa), ma questa proprietà di R risulta pure definibile al secondo ordine.

Il teorema di completezza che correla [1] a [2] mostra come la tendenza alla generalizzazione abbia guidato i maggiori progressi in campo modale. Sono diverse in effetti le direzioni in cui si è cercato di generalizzare i primi risultati di Kripke.

Sul piano semantico è sufficiente ricordare che una semantica più generale di quella a mondi possibili è la semantica a intorni (neighbourhood semantics). Una struttura a intorni è una coppia 〈W,N〉 dove W è un insieme di mondi e N una funzione che associa a ogni mondo w di W un insieme di sottoinsiemi di W. □A si dirà vera in un mondo w° di W se e solo se l'insieme dei mondi in cui è vera A è uno degli insiemi di N(w°). Tutte le strutture relazionali possono essere convertite in strutture a intorni equivalenti definendo N(w°) come la classe di tutti gli insiemi che contengono {w_j: w°Rw_j}, ma la conversione non è reciproca.

Un altro tipo di generalizzazione semantica riguarda non il supporto W ma le relazioni di accessibilità: le relazioni diadiche possono essere viste come casi speciali di relazioni con più di due posti, oppure come relazioni tra insiemi di mondi anziché tra singoli mondi.

Sul piano linguistico-sintattico sono stati studiati diversi modi per arricchire il linguaggio modale di base, modi che ovviamente si riflettono anche sulle proprietà dei modelli associabili.

(a) Estensione del linguaggio con costanti proposizionali. Per esempio, introducendo la costante proposizionale Q, opportunamente assiomatizzata col senso di 'non ci sono trasgressioni al codice morale', si può rendere la nozione di 'obbligatorio OA' mediante □(Q⊃A). In questa logica (detta deontica) non varrà la legge OA⊃A, ma solo la più debole OA⊃∉O∉A.

(b) Estensione del linguaggio con esponenti esprimenti gradi di necessità. □ⁿA si leggerà 'A è necessaria al grado n'. Con opportuni assiomi per l'additività questa logica si trasforma in una logica modale probabilistica.

(c) Impiego di operatori modali primitivi a due, tre o più posti. Devono consentire la definizione di □ e  senza essere riducibili a questi. Un esempio di logica modale con un primitivo diadico è la cosiddetta logica condizionale. All'origine di questa logica stanno ben note difficoltà nell'analisi dei condizionali controfattuali. Per esempio, la forma dell'enunciato 'se il naso di Cleopatra fosse stato più lungo Roma non avrebbe conquistato l'Egitto' non può essere quella di un condizionale materiale (perché risulterebbero veri tutti i condizionali con antecedenti falsi, quindi tutti i controfattuali) e nemmeno quella dell'implicazione stretta, dato che l'antecedente non implica necessariamente il conseguente. Secondo David K. Lewis la verità di un condizionale siffatto si stabilisce ispezionando i mondi più simili al nostro in cui Cleopatra ha un naso più lungo di quello attuale e chiedendoci se in questi è vero il conseguente. Un condizionale A□→B si dirà vero in un mondo w° se e solo se B è vera nei mondi in cui è vera A e per il resto più simili a w°. □A è definibile in questo linguaggio come ∉A□→A. Una semantica formale per questo calcolo è data da modelli 〈W,R, f ,V〉 dove f è una funzione selettiva che sceglie dentro i mondi accessibili, per ogni antecedente A e mondo w°, un insieme di mondi f(A,w°) (intuitivamente, i più simili a w°) in cui è vera A. Se la classe dei mondi selezionata da f contiene un solo mondo (secondo la proposta originaria di Robert C. Stalnaker) si ottiene la legge del terzo escluso condizionale A□→B A□→∉B, respinta da Lewis. Anche i modelli di Stalnakercomunque falsificano tre leggi di solito considera-te inattaccabili per i condizionali, tra cui transiti-vità: (A□→B B□→C)⊃(A□→C); contrapposizione: A□→B∉B□→∉A; monotònicità: A□→B⊃((A C)□→B).

Nei casi in cui il condizionale non è controfattuale ma fattuale (indicativo), cioè in cui è vero A B A□→B, questi sistemi hanno la spiacevole caratteristica di generare il collasso di A□→B sul condizionale materiale A⊃B. L'insoddisfazione per questo risultato ha incoraggiato ricerche volte a cogliere un nesso di rilevanza o consequenzialità tra le clausole.

(d) Estensione a linguaggi dotati di più operatori modali. Questo tipo di estensione produce la famiglia delle logiche dette multimodali, entro la quale le logiche modali classiche si possono considerare un caso speciale. La più studiata delle logiche multimodali è la logica dei tempi verbali, dovuta a Arthur N. Prior (1951). In questa gli operatori primitivi sono H e G, da leggere 'sempre in passato' e 'sempre in futuro', mentre i loro duali sono P e F, ossia 'qualche volta in passato' e 'qualche volta in futuro'. Nel sistema minimale K_t avremo due assiomi in H e G paralleli all'assioma monomodale K, ma sono richiesti anche assiomi misti come FHA⊃A e PG A⊃A, oltre a due regole ⊦A→⊦GA e ⊦A→⊦HA. Un problema aperto da questi sistemi riguarda la definizione che si può dare dell'operatore di necessità, e qui la risposta può variare perché disponiamo della nozione di tempo diodorea (□A=GA A) e di quella detta aristotelica (□A=GA A HA). Contrariamente a quanto congetturato inizialmente da Prior, il sistema per la necessità diodorea non è S4 ma un sistema più forte S4.3 (S4+□(□(A⊃□A)⊃A)⊃(□A⊃A)) se si assume il tempo discreto, o S4.3.1 (S4+□(□A⊃□B) □(□B⊃□A)) se si assume il tempo continuo.

I modelli temporali sono modelli con due relazioni di accessibilità 〈T,R¹,R²,V〉, dove T è un insieme di istanti, R¹ e R² hanno le proprietà delle relazioni 'prima' e 'dopo' oltre ad altre dipendenti dalle caratteristiche del medium temporale che vengono presupposte. Una variante interessante della semantica temporale si ha assumendo come elementi di base non gli istanti ma gli intervalli, con una evidente complicazione nel determinare le relazioni di accessibilità tra questi.

Le logiche multimodali sono state negli anni Novanta la frontiera più avanzata della ricerca modale. Il progresso è stato evidente nella logica cosiddetta epistemica, in cui la necessità coincide con l'essere conosciuto e i mondi possibili con stati di conoscenza ordinabili per maggiore o minore profondità. Per fare un esempio, se K è un operatore tale che KA significa 'è conosciuto che A' e BA significa 'è creduto che A', ciascuno di questi operatori può essere indicizzato da i,j,… in modo tale che K_iA significa 'l'agente i conosce A' e B_iA significa 'l'agente i crede che A'. Si sviluppano in questo modo logiche epistemiche e doxastiche variamente assiomatizzate. A livello semantico diventano descrivibili processi multiagenti e relazioni di accessibilità tra agenti, che possono essere non solo esseri umani ma computer. Casi speciali di logiche multimodali pure collegabili all'informatica sono le logiche dinamiche, in cui occorrono operatori indicizzati di forma □a ‒ dove a è un programma ‒ e tali che □aA viene letto 'A vale dopo ogni esecuzione di a'. I mondi sono in questo caso stati di un computer e le relazioni indicizzate da programmi descrivono possibili transizioni di stato.

Si noti che l'indicizzazione degli operatori modali si può applicare illlimitatamente ad altri linguaggi, come quello della logica deontica o temporale. Definendo operazioni sugli indici e ‒ a livello semantico ‒ operazioni sulle relazioni di accessibilità, si consegue una trattazione astratta delle logiche multimodali, che ha consentito di dimostrare un teorema generale di completezza per queste.

La trattazione multimodale apre anche una nuova prospettiva circa la quantificazione. Mentre fin dall'inizio gli operatori modali sono stati considerati tipi particolari di quantificatori (al punto che, come si è visto, si è loro negata una fisionomia autonoma), ora è possibile rovesciare questo rapporto trattando i quantificatori come tipi particolari di operatori modali indicizzati. Se, per esempio, v(i) è l'i-esima variabile, ∃v(i)A si può trattare in un particolare linguaggio multimodale come l'asserto v(i)A.

L'affinità strutturale tra quantificatori e operatori modali può spiegare molte difficoltà originate dal loro impiego congiunto, quale si incontra nella logica modale del primo ordine con o senza identità. A meno di non introdurre assiomi riduttivi come la cosiddetta formula Barcan ∃xPx≡∃xPx, è apparso a molti chiaro che c'è una differenza tra fare l'asserto de re ∃xPx (per es. 'c'è qualcuno che può vivere 150 anni') e fare l'asserto de dicto ∃xPx ('è possibile che sia vero che qualcuno viva 150 anni'): differenza che risalta soprattutto dando una lettura temporale della possibilità. La formula Barcan corrisponde alla poco plausibile assunzione semantica per cui c'è un unico dominio di individui invariante per tutti i mondi possibili. Rifiutando questo assunto però non c'è un modo univoco e intuitivo per associare i domini di individui ai mondi possibili. Una scelta consiste nel richiedere che, se w_iRw_j, il dominio D_i associato a w_i sia incluso nel dominio D_j associato a w_j. Una proposta diversa, dovuta a Kripke, consiste nell'evitare di agganciare l'accessibilità all'inclusione tra domini e nel far variare le variabili libere su un unico dominio universale D, di cui i vari D_i sono sottoinsiemi, mentre le variabili quantificate continuano a spaziare su domini indicizzati da mondi. L'inconveniente di questa proposta è che così si deve abbandonare la legge di specificazione ∀xPx⊃Py, che è un cardine dalla logica quantificata standard. Queste difficoltà ovviamente condizionano anche il modo di trattare l'identità, soprattutto quando oltre ai nomi propri vengono ammesse le descrizioni definite. Se si dice per esempio □(il sindaco di Milano=il sindaco di Milano), questa è l'esemplificazione di una legge logica; ma la sua quantificazione de re ∃x□(x=il sindaco di Milano) fa pensare che ci sia qualcuno che in ogni mondo possibile è sindaco di Milano, mentre la de dicto □∃x(x=il sindaco di Milano) fa pensare che l'esistenza di un sindaco di Milano sia una verità necessaria: due tesi difficili da sostenere.

La logica modale quantifcata ha offerto strumenti raffinati per l'indagine filosofica e linguistica, ma si è rivelata una fonte di problemi di ardua soluzione. Un fondamentale risultato di Silvio Ghilardi (1990) raggiunto con metodi derivati dalla teoria delle categorie, ha dimostrato che, mentre i risultati di incompletezza rispetto a strutture relazionali sono sporadici a livello proposizionale, c'è un numero infinito di sistemi modali incompleti tra S4 e S5 quantificazionali. Questo risultato costringe a mettere in discussione l'attendibilità della stessa semantica relazionale, ponendo con forza il problema di una sua revisione o addirittura di un suo superamento.

Logiche più deboli della logica standard

La seconda classe di logiche da esaminare contiene logiche il cui insieme di tesi è rappresentabile come un sottoinsieme proprio dell'insieme delle tesi standard. Questa caratterizzazione sintattica consente di evitare, almeno in prima approssimazione, la questione se il significato di alcuni o tutti i connettivi che compaiono nel linguaggio di questi sistemi sia lo stesso di quello standard o traducibile in questo (si pensi allo slogan di Quine change of logic, change of subject). La legge logica classica che ha suscitato più riserve (già nell'antichità: si veda il famoso passo De interpretatione, 9, di Aristotele sui futuri contingenti) è stato indubbiamente il principio del terzo escluso. Nella prospettiva intuizionista di Luitzen E.J. Brouwer la verità matematica di una proposizione A coincide con l'esistenza di una dimostrazione di A. Stante l'esistenza di casi in cui non si dà né una dimostrazione di A né di ∉A, si impone un abbandono del principio del terzo escluso. Lo stesso risultato è inevitabile in tutte le concezioni dette costruttive della logica. Nella logica operativa di Paul Lorenzen, per esempio, una costruzione per A è un dialogo in cui falliscono tutti i tentativi di attaccare A; e il sistema che si ottiene, anche se presentato sotto forma di gioco dialogico, contiene tesi accettabili per un intuizionista.

Nella logica intuizionista IPC formalizzata da Arend Heyting nel 1930 non vale la legge A ∉A, anche se vale la bivalenza nella formula A→∉∉A ma non la conversa ∉∉A→A. Come ha provato Kripke, il sistema IPC pur essendo più debole della logica classica può essere però rappresentato entro il sistema di logica modale S4 che, come si è visto, è un'estensione della logica standard. I mondi dei modelli relazionali per questa logica sono interpretati come stati di conoscenza ordinati dalla relazione di inclusione ⊆. Si dirà che A→B è vera in uno stato i se e solo se A è vera solo se B è vera in tutti gli j tali che i⊆j.

I rapporti tra logica intuizionista e logica modale sono complessi. Sia A* la traduzione che interpreta A come □A nel senso 'A è dimostrabile nell'aritmetica' e A→B come □*A⊃□*B. Se chiamiamo GRz l'assioma di Grzegorczyc □(□(A→□A)→A)→A, si può far vedere che, per ogni formula A del calcolo intuizionista di Heyting, ⊦_IPCA se e solo se ⊦_SA* per ogni S intermedio tra S4 e S4+GRz. Altri risultati riguardano le logiche cosiddette intermedie, che sono più deboli della classica e più forti dell'intuizionista. Al proposito è acclarato che esistono 2^ℵ_° logiche intermedie che formano un reticolo distributivo ordinato dalla relazione di inclusione impropria. Oltre a queste ricerche vanno ricordati gli studi sui rapporti tra la logica intuizionista e la logica minimale di Johansson (1939) che esclude, oltre al terzo escluso, anche la formula classica ∉A→(A→B).

Da un punto di vista semantico, è degno di nota che la logica intuizionista segna un mutamento nell'impiego della nozione di mondo possibile, che ora viene identificato con uno stato di informazione più o meno incompleto. Questo mutato atteggiamento non è un fenomeno isolato. Il passaggio dalla nozione di istante a quella di intervallo (elemento di informazione incompleta circa la collocazione precisa di un istante) nella logica temporale e il passaggio da una semantica bivalente a una che ammette lacune di valore di verità nella logica dei quantificatori sono manifestazioni parallele di una tendenza che è stata chiamata orientamento verso la parzialità. La semantica dei dati di Frank Veltman (1981), la semantica situazionale di Jon Barwise e John Perry (1983), la semantica a possibilities di Lloyd Humberstone (1981) sono basate su modelli parziali in cui invece di mondi ci sono frammenti di mondo variamente connotati.

Un posto particolare tra le logiche più deboli della logica classica spetta alle cosiddette rilevanti di Alan R. Anderson e Nuel D. Belnap (1958), che sono classificabili nella categoria delle logiche dette sottostrutturali. Tali logiche si caratterizzano per essere prive di una o più regole strutturali classiche, cioè delle regole inferenziali fondamentali che non coinvolgono connettivi specifici (per es. indebolimento, contrazione, permutazione). Le leggi classiche incriminate dai seguaci della logica rilevante sono quelle che impediscono di caratterizzare → come un rapporto di implicazione in cui sia l'antecedente effettivamente usato per derivare l'antecedente: prima fra tutte la legge della rilevanza A→(B→A), vista come esemplare fallacia della rilevanza, e la connessa regola strutturale A⊦C / A,B⊦C. La logica dell'implicazione stretta da questo punto di vista non è soddisfacente perché ammette dei teoremi come (A ∉A)aB, in cui il nesso di rilevanza chiaramente non sussiste. Il linguaggio della logica rilevante può avere come primitivo il solo → ma può essere esteso anche ai connettivi classici, dando origine alla logica rilevante dispiegata R. La nozione di necessità □A può essere definita come (A→A)→A. Se vogliamo cogliere l'idea che il nesso implicativo sia, oltre che rilevante, necessario, tuttavia bisogna eliminare la legge di permutazione (A→(B→C))→(B→(A→C)) (che porta, come è facile vedere, a A→□A) e restringerla alle sole formule implicative, in modo da ottenere (A→B)→□(A→B). Il sistema così ottenuto, E, è detto dell'entailment o implicitazione.

Il motivo per cui queste logiche hanno avuto un seguito limitato è che l'abbandono di alcune regole sottostrutturali porta a conseguenze controintuive, come l'esclusione del sillogismo disgiuntivo ∉A→(A B), da cui deriva l'indesiderata formula (A ∉A)→B. Questa esclusione si può difendere solo sostenendo che ∉, , hanno un senso diverso da quello verofunzionale.

A questi dubbi si aggiungono le stranezze della semantica associata alle logiche rilevanti, che Richard Routley e Robert K. Meyer (1972) hanno formulato impiegando una relazione di accessibilità triadica la quale, come è stato subito osservato, è analoga alla relazione di collinearità tra i punti di un piano. Questa analogia ha aperto la strada al sorprendente teorema con cui Alasdair Urquhart ha dimostrato l'indecidibilità di R, E e di infinite logiche rilevanti prive di negazione.

In effetti la logica rilevante è solo una delle molte logiche implicative non standard proposte nel XX secolo. Altre implicazioni non standard sono l'implicazione analitica di William T. Parry, l'implicitazione di Georg H. von Wright, Kanger e Keith Lehrer, l'implicazione connessiva di Thomas Nelson, Richard B. Angell e McCall. Quest'ultima è basata su due principi che non sono classici: ∉(A→∉A) e (A→B)⊃∉(A→∉B), e si devono quindi collocare nella terza classe di logiche non standard. Tuttavia è stato recentemente dimostrato che se → è interpretato come una speciale implicazione stretta in cui le due clausole hanno identico status modale (implicazione consequenziale), i principi più caratteristici dell'implicazione connessiva si traducono in teoremi modali del sistema KT. In tal modo i principi suddetti vengono trasferiti entro una logica modale decidibile e si getta un ponte verso le logiche condizionali, che sono pure estensioni della logica standard.

Logiche divergenti dalla logica standard

Molti dei problemi discussi nei paragrafi precedenti suggeriscono eventuali modifiche dei sistemi in oggetto che li rendono inconfrontabili con la logica standard. Un semplice esempio è offerto da logiche modali che si ottengono aggiungendo gli assiomi modali non al calcolo classico ma a quello intuizionista: questo evidentemente comporta indebolimenti di alcune leggi modali e, sul piano semantico, una modellizzazione più complessa con due relazioni di accessibilità.

In modo analogo si possono ottenere un numero arbitrariamente ampio di logiche modali quantificate in cui gli assiomi modali sono aggiunti non alla logica standard ma a a sistemi più deboli, detti di logica libera (free logic), in cui si ammettono termini che non denotano enti realmente esistenti. In tali sistemi cade la legge classica A(a/x) ⊃∃xA che, introducendo la definizione E!a=_Def∃x(x=a) viene indebolita in (A(a/x) E!a)⊃∃xA. Questo ci impedisce di passare da Pegaso=Pegaso a 'c'è qualcosa che è Pegaso', anche se la presenza di operatori modali nel linguaggio ci consente di parlare di esistenza possibile di Pegaso.

Logiche come quelle ora richiamate non rientrano dunque né nella prima né nella seconda classe di logiche non standard. A proposito della tripartizione proposta va tuttavia osservato che mentre ogni logica singolarmente presa deve rientrare in una delle tre categorie definite, può accadere che questo non valga per famiglie di logiche con caratteristiche comuni. Data una famiglia di logiche F, può accadere che alcune delle logiche di F siano incompatibili con la logica standard, mentre altre risultano ricostruibili come sottosistemi o soprasistemi della stessa. Il ruolo giocato dal linguaggio nel determinare queste appartenenze è essenziale. Molti sistemi logici risultano inconfrontabili con quelli standard perché presentano un linguaggio dotato di primitivi essenzialmente diversi da quelli standard. In questa classe si possono collocare le logiche lineari, in cui le ipotesi sono viste come risorse che possono essere consumate al massimo una volta in una dimostrazione. Ogni connettivo ha una versione moltiplicativa e una additiva, che corrisponde alla presenza simultanea e alternativa delle risorse. L'implicazione lineare A-0B indica che si consuma la risorsa A per acquisire la risorsa B. Recenti tentativi di modellizzare la logica lineare mediante modelli alla Kripke con R triadica segnalano la concreta possibilità di ricondurre le logiche lineari alla famiglia delle logiche modali e delle logiche rilevanti. Per un altro verso, le logiche lineari vengono spesso assegnate alla classe delle logiche sottostrutturali in quanto comportano la rinuncia a una regola strutturale come la regola di contrazione A,A⊦B / A⊦B.

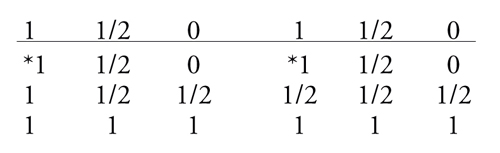
Tutte le logiche considerate nei paragrafi 1 e 2 si possono considerare logiche dotate di una semantica che, a meno di lacune nei valori di verità, è rigidamente bivalente. Ma l'abbandono della bivalenza ha segnato indubbiamente una svolta nella ricerca logica già negli anni Venti. Nel 1921 Émil Post formulava l'idea di logiche con più di due valori di verità, idea poi ripresa sistematicamente da Jan Łukasiewicz negli anni Venti e Trenta. La più semplice logica polivalente ha tre valori di verità (1,0,1/2): secondo il progetto iniziale di Łukasiewicz il terzo valore (indeterminato) aveva la funzione di impedire una visione deterministica del futuro che potrebbe essere sollecitata dalla bivalenza stretta, mentre in un secondo tempo il valore 1/2 viene letto come 'né vero né falso' o 'possibile'. Le matrici da lui introdotte per → e ∉ sono le seguenti (dove * contrassegna il valore designato)

A B viene definito da Łukasiewicz come (A→B)→B, mentre l'operatore di possibilità A è definito come ∉A→A. Mentre il frammento non modale di questi calcoli risulta un sottosistema di quello standard, il suo frammento modale ha caratteristiche atipiche, come si vede dal teorema ∉A→∉A, che nella logica modale classica comporterebbe il collasso del falso sull'impossibile. L'insieme delle leggi modali di questo sistema è in ogni caso inesprimibile nella logica standard.

È immediato osservare che le matrici trivalenti di Łukasiewicz non sono le uniche possibili. Le seguenti per l'implicazione sono dovute rispettivamente a Stephen C. Kleene (1938) e Dimitrij Bochvar (1939):

La differenza con le matrici di Łukasiewicz è spiegata da una diversa interpretazione del terzo valore. Per Kleene 1/2 significa indecidibile (si applica quindi alle proposizioni indecidibili dell'aritmetica), mentre 1/2 per Bochvar significa paradossale e si applica quindi alle proposizioni antinomiche tipo mentitore. Bochvar introduce nella sintassi anche un connettivo V con il senso di 'è asserito che' tale che VA prende valore 0 per A=1/2 e coincide con A per 0 e 1. Grazie a V si possono definire dei connettivi esterni ∉, , , → che hanno il comportamento bivalente standard, introducendo quindi uno sdoppiamento linguistico dei connettivi.

Molte tavole trivalenti sono state proposte per nozioni non trattabili in termini di bivalenza rigida: tale per esempio la nozione di privo di senso e la nozione di qualcosa che è inaffermabile per assenza degli oggetti a cui si fa riferimento in un dato periodo temporale (sistema Q di Prior).

La logica trivalente di Łukasiewicz ha avuto applicazioni interessanti diverse da quelle da lui intese, come ha mostrato Hans Reichenbach nella trattazione della meccanica quantistica. In questo contesto è assegnato un terzo valore di verità alle proposizioni in cui si esprime la misura simultanea di grandezze coniugate, impiegando tavole che estendono quelle di Łukasiewicz con più tipi di negazione e di implicazione. Nel 1936 Garrett Birkhoff e John von Neumann introducevano, ancora per lameccanica quantistica, una logica alternativa in cui continua a valere A ∉A mentre vengono meno alcuneleggi distributive (cioè ((A B) (A C))→(A (B C)) e ((A B) C)→((A C) (B C)). In questa logica la verità di una disgiunzione non implica la verità di uno dei disgiunti. Per misurare la distanza dall'implicazione classica si noti che l'implicazione quantistica A→B viene normalmente introdotta per definizione come ∉A (A B). In lavori più recenti di Herman Dishkant e Maria Luisa Dalla Chiara si è provato che la negazione quantistica è rappresentabile come negazione classica necessitata e che l'implicazione quantistica è rappresentabile come un tipo particolare di implicazione stretta. In altri sistemi quantistici si è impiegato direttamente un operatore condizionale analogo a quello di Stalnaker-Lewis, collocando quindi questa logica nel quadro delle logiche modali.

Le tavole trivalenti sopra esposte si possono vedere come casi speciali di tavole con infiniti valori nell'intervallo [0,1], il che porta le semantiche per le logiche polivalenti ad approssimarsi alla semantica probabilistica. Ma ultimamente un modo diverso di usare infiniti valori ha ricevuto un impulso per opera della cosiddetta logica sfumata o fuzzy logic. Mentre l'atteggiamento della logica tradizionale consiste nel rifiuto di importare nei sistemi formali la vaghezza del linguaggio ordinario, quella sfumata parte da presupposti diversi: la teoria degli insiemi su cui si basa è essa stessa sfumata, ammettendo infiniti gradi di appartenenza a un insieme. Due insiemi sfumati si diranno identici se gli stessi oggetti appartengono a essi con lo stesso grado di appartenenza. I connettivi logici riproducono le operazioni insiemistiche e la logica che ne risulta ammette infiniti valori intermedi tra 0 e 1. La logica sfumata ha proprietà sfumate, tavole di verità sfumate e regole di inferenza sfumate, rendendo evanescente l'applicazione dei concetti tradizionali di assiomatizzabilità, consistenza, completezza. Tali proprietà peraltro interessano relativamente i cultori della fuzzy logic, poiché il loro obiettivo preminente è stata l'applicabilità pratica di questa logica che di fatto ha avuto un durevole successo applicativo.

Negli stessi anni in cui veniva sviluppata la fuzzy logic, il logico brasiliano Newton da Costa, partendo da idee anticipate degli anni Trenta da Nicolai Vasiliev e Stanislaw Jaskowski, dava impulso a una nuova logica, la logica paraconsistente, il cui obiettivo era quello di creare sistemi che ammettono contraddizioni senza perciò essere banalizzati dalla cosiddetta legge dello Pseudo-Scoto (A ∉A)→B. Le logiche paraconsistenti sono logiche non-scotiane che hanno queste caratteristiche:

(a) risulta invalido il principio di non-contraddizione ∉(A ∉A);

(b) in generale, se due qualsiasi formule sono tra loro incompatibili, non deve essere possibile derivare una qualsiasi formula A;

(c) i sistemi costruiti devono contenere il maggior numero possibile dei teoremi del calcolo standard compatibili con (a) e (b).

Si noti che (a) non elimina automaticamente il terzo escluso, che risulta un teorema nel sistema minimale C1 di da Costa e nella gerarchia di sistemi costruiti su questo. Dato il ruolo decisivo avuto dall'antinomia di Russell nella crisi dei fondamenti, è stato naturale costruire anche una teoria paraconsistente degli insiemi (su base trivalente). Ma le implicazioni filosofiche sono state altrettanto interessanti: da un lato la logica paraconsistente è imparentata con la logica rilevante (che è una logica non scotiana), dall'altro si è comprensibilmente sviluppata una tendenza a passare dalla logica paraconsistente a quella dialettica ispirata da Georg Wilhelm Friedrich Hegel e Karl Marx. In questa direzione, Graham Priest (1979) ha elaborato una semantica trivalente uguale a quella di Bochvar salvo per il fatto che ci sono due valori designati: vero e paradossale.

La logica paraconsistente dunque tollera contraddizioni, le quali costituiscono un inevitabile ‒ e secondo alcuni indispensabile ‒ aspetto della crescita della conoscenza. Ma i conflitti cognitivi nello studio della dinamica delle teorie hanno rappresentato per la logica una sfida che è stata affrontata in modi diversi. Nella cosiddetta belief revision si ammette la possibilità che una nuova informazione entri in conflitto con vecchie informazioni, ma questo si risolve non nell'accettare le contraddizioni ma nell'eliminare la parte delle vecchie conoscenze incompatibile con la nuova. Questa linea di ricerca ha un impatto sulla natura della logica perché, dato un certo numero di premesse, va preso atto che la crescita dell'informazione, o anche il miglioramento di un'ipotesi precedentemente avanzata, può esigere la sostituzione di una precedente conclusione A con la conclusione ∉A: siamo di fronte al fenomeno della non monotònicità dell'inferenza.

Come abbiamo già visto, la monotònicità viene esclusa dalle proprietà dei condizionali controfattuali, che però sono trattati nella logica condizionale come operatori modali diadici. Qui si tratta invece di individuare logiche in cui la stessa relazione di conseguenza metasistematica sia non monotòna. Ciò accade in particolare nel ragionamento per default (quando si assume che qualcosa è vero solo per mancanza di evidenza contraria) o nel ragionamento abduttivo (quando si conclude qualcosa perché è la migliore spiegazione possibile dei dati disponibili). Si noti peraltro che la non-monotònicità caratterizza anche il ragionamento induttivo e quindi anche la variegata classe delle logiche, di solito studiate come estensioni assiomatiche della logica standard, note come logiche induttive. È possibile trattare l'inferenza non-monotòna in vari modi, due dei quali hanno suscitato un certo interesse. Il primo consiste nell'estendere il linguaggio della logica del primo ordine con un operatore modale M che consente di formulare regole di forma B MB′ / B′ ('Se Titty è un uccello ed è consistente che Titty possa volare, allora Titty vola'). Nel secondo approccio si formulano le regole di default in termini di normalità (∉Ab) come B ∉AbB / B′ ('Se Titty è un uccello ed è un normale uccello, allora Titty vola').

Essendo oggetto di ricerche promosse per lo più da informatici, le logiche non-monotòne (così come le logiche lineari, le logiche dinamiche e alcuni sistemi di logica temporale) si possono considerare un prodotto dell'interscambio sempre più intenso tra logica e informatica, e fanno parte di un'area di ricerca il cui sviluppo è destinato a segnare rapidi e incisivi progressi.

Bibliografia

Una bibliografia completa sulle logiche non standard si può ricostruire consultando le bibliografie contenute nelle seguenti opere generali:

Gabbay, Guenthner 1986: Handbook of philosophical logic, edited by Dov Gabbay, Franz Guenthner, Dordrecht-Lancaster, Reidel, 1986, 4 v.

Haack 1974: Haack, Susan, Deviant logic, London, Cambridge University Press, 1974.

Klibanski 1968-1971: Contemporary philosophy. A survery, edited by Raymond Klibanski, Firenze, La Nuova Italia, 1968-1971.

Bencivenga 1986: Bencivenga, Ermanno, Le logiche libere, Torino, Boringhieri, 1986.

Bräuner, Ghilardi 2006: Bräuner, Torben - Ghilardi, Silvio, First order modal logic, in: Handbook of modal logic, edited by Patrick Blackburn, Johan van Benthem, Frank Wolter, Amsterdam, Elsevier, 2006.

Carnap 1947: Carnap, Rudolf, Meaning and necessity, Chicago, University of Chicago Press, 1947.

Carnielli, Pizzi 2001: Carnielli, Walter - Pizzi, Claudio, Modalità e multimodalità, Milano, Angeli, 2001.

Chellas 1980: Chellas, Brian F., Modal logic: an introduction, Cambridge-London, Cambridge University Press, 1980.

Da Costa 1980: Da Costa, Newton C.A., Ensayo sobre os fundamentos da lógica, São Paulo, Hucitec, 1980.

Dalla Chiara, Giuntini 1997: Dalla Chiara, Maria Luisa - Giuntini, Roberto, La logica quantistica, in: Filosofia della fisica, a cura di Giovanni Boniolo, Milano, Bruno Mondadori, 1997.

Fischer Servi 2001: Fischer Servi, Gisele, Quando l'eccezione è la regola. Le logiche non monotone, Milano, McGraw-Hill, 2001.

Fitting 1983: Fitting, Melvin, Proof methods for modal and intuitionistic logic, Dordrecht-Lancaster, Reidel, 1983.

Girard 2004: Girard, Jean-Yves, Lectures on proof-theory, Roma Tre, october-december 2004.

Hughes, Cresswell 1990: Hughes, George E. - Cresswell, Maxwell J., Guida alla logica modale, Bologna, Clueb, 1990 (ed. orig.: A companion to modal logic, London, Methuen, 1984).

Kosko 1994: Kosko, Bart, Il fuzzy- pensiero, Milano, Baldini & Castoldi, 1994 (ed. orig.: Fuzzy-thinking, London, Harper Collins, 1993).

Lewis 1973: Lewis, David K., Counterfactuals, Oxford, Blackwell, 1973.

Lewis, Langford 1932: Lewis Clarence I. - Langford, Harold C., Symbolic logic, New York, Dover, 1932.

Marsonet 1976: Marsonet, Michele, Introduzione alle logiche polivalenti, Roma, Abete, 1976.

Pizzi 1974: La logica del tempo, a cura di Claudio Pizzi, Torino, Boringhieri, 1974.

Pizzi 1978: Leggi di natura, modalità, ipotesi, a cura di Claudio Pizzi, Milano, Feltrinelli, 1978.

Pizzi 1987: Pizzi, Claudio, Dalla logica della rilevanza alla logica condizionale, Roma, Euroma stampa, 1987.

Silvestrini 1979: Individui e mondi possibili, a cura di D. Silvestrini, Milano, Feltrinelli, 1979.

Van Benthem 1983: Van Benthem, Johan F.A., Modal logic and classical logic, Napoli, Bibliopolis, 1983.

Van Benthem 1985: Van Benthem, Johan F.A., A manual of intentional logic, Stanford, CSLI, 1985.