Musica elettronica ed elettronica musicale
Musica elettronica ed elettronica musicale
A partire dalla fine dell’Ottocento fino alla Seconda guerra mondiale, grazie alla diffusione dell’elettricità e dell’elettronica, fanno la loro comparsa nuovi strumenti musicali elettroacustici che producono note con un timbro fisso caratteristico dello strumento, non diversamente dagli strumenti tradizionali. Il Singing arc di William Duddell (Regno Unito, 1899) è basato sul ronzio delle lampade ad arco per illuminazione stradale; il Thelarmonium (Thaddeus Cahill, Stati Uniti, 1900), diffonde via telefono una musica prodotta da generatori elettrici di tensioni alternate a differenti frequenze; il Theremin (Lev Sergeevič Termen, Russia, 1917), ancora oggi in uso, è basato su circuiti eterodina a radiofrequenza a valvole termoioniche, le cui frequenze e ampiezze di oscillazione sono modulabili dall’esecutore avvicinando e allontanando le mani da due antenne dello strumento.
La celebre macchina Onde Martenot (Maurice Martenot, Francia, 1928) utilizza il cuore del Theremin, organizzandolo però attorno a una tastiera munita di controlli per intensità, vibrato e glissando. L’organo Hammond (Laurens Hammond, Stati Uniti, 1929), il cui successo si prolunga fino al secondo dopoguerra, utilizza un’evoluzione della tecnologia del Thelarmonium. Il Trautonium (Friedrich Trautwein, Germania, 1930), come la sua evoluzione nel Mixtur Trautonium (Oskar Sala), è commercializzato dalla Telefunken dopo il 1932 e consiste di oscillatori a tubi al neon controllati da una tastiera. A questa fase storica appartiene anche il Vocoder di Homer Dudley (Voice operated recorder; Stati Uniti, 1939). Pur essendo uno strumento per l’analisi e la resintesi del parlato per ricerche sulla compressione delle conversazioni telefoniche, si è guadagnato fin dall’inizio l’interesse di musicisti e compositori, soprattutto tedeschi. Una versione solo sintetizzante, il Voder, fu mostrata alla Fiera mondiale di New York del 1939: azionata da una tastiera, produceva parole intelligibili per la meraviglia del pubblico.
Nel secondo dopoguerra l’evolversi della miniaturizzazione elettronica − si passa dai tubi a vuoto ai dispositivi a semiconduttore − e la diffusione della radio e dei mezzi di riproduzione (grammofoni, magnetofoni) aprono una nuova fase. Si compone musica per la radio e per nastro magnetico, generando il suono mediante oscillatori o registrandolo con grammofoni e magnetofoni e infine trasformandolo in studio con tecniche di montaggio (collage, missaggio, trasposizione, riverbero).
Compariranno in seguito i sintetizzatori analogici, strumenti configurabili per la sintesi e l’elaborazione del suono, tra i quali ricordiamo il Melochord di Harald Bode (Germania, 1949), lo RCA Synthesizer (Harry Olsen e Herbert Belar, Stati Uniti, 1952) e attorno agli anni Sessanta i sintetizzatori di Robert A. Moog (che ebbero un notevole successo commerciale) e di Donald Buchla.
A partire dalla fine degli anni Cinquanta la diffusione dell’elettronica numerica segna il passaggio dalla musica elettronica alla computer music. Inizialmente si usa un calcolatore elettronico per generare partiture tradizionali secondo schemi formali ed estetici definiti dal compositore-programmatore. In seguito − con il progredire delle potenze di calcolo − i sistemi numerici soppianteranno i dispositivi analogici per la sintesi e l’elaborazione del suono.
Oggi è l’epoca della software music: le tecnologie della computer music sono state trasferite in programmi di calcolo, privi di uno specifico riferimento a un supporto materiale, adatti a calcolatori per usi generali.
Gli albori della computer music
Negli anni Cinquanta i calcolatori elettronici numerici disponibili avevano una potenza di calcolo nemmeno lontanamente sufficiente a sintetizzare o elaborare il suono in tempo reale. Il loro uso si è quindi inizialmente limitato alla produzione di suoni in elaborazione differita, alla supervisione di strumenti elettronici analogici o ancora alla generazione di partiture tradizionali, di note, su base algoritmica.
I sistemi per la composizione algoritmica
La generazione di partiture al calcolatore introduce nella composizione delle forme musicali gli algoritmi, la cui concezione entra dunque a far parte del pensiero compositivo giocandovi un ruolo stilistico. Dopo il linguaggio di programmazione per la composizione MUSICOMP di Lejaren Hiller (Stati Uniti, fine anni Cinquanta), nel 1962 comparirà ST di Yannis Xenakis. Quest’ultimo genera partiture sulla base di meccanismi casuali entro predefinite strutture ritmiche e di intonazione seguendo distribuzioni statistiche assegnate, secondo una cifra estetica caratteristica del compositore. Due anni dopo, presso lo studio dell’Università di Utrecht in Olanda, Gottfried Micheal Koenig svilupperà Project 1, un generatore di contrappunti di serie di note e di durate secondo regole strettamente deterministiche che si riferiscono alla scuola del serialismo integrale (o strutturalismo). In seguito, attorno al 1972, Koenig stesso si rivolgerà con SSP alla generazione del suono.
I primi sistemi software per la generazionee composizione dei suoni
Già nel 1957, Max Mathews intuiva le grandi potenzialità dei sistemi numerici per la generazione del suono. Presso i Bell Laboratories, perfezionerà infatti nel corso degli anni un linguaggio di programmazione per la generazione in differita del suono, MUSIC 1, scritto in Assembler su di un calcolatore a valvole ed evolutosi fino al MUSIC V (scritto in FORTRAN IV), poi al MUSIC 360 (per i sistemi IBM 360, 1969) e al MUSIC 11 (per i sistemi DEC PDP 11, 1973). Mathews inaugura così la computer music, la musica elettronica in veste numerica. La serie MUSIC può essere considerata la progenitrice del c-sound, un linguaggio ancora oggi usato da molti compositori per la generazione di musica in differita e, recentemente, anche in tempo reale.
La grande attrattiva del calcolatore elettronico sta nella possibilità di memorizzare algoritmi di generazione del suono in repertori riutilizzabili ma sempre modificabili (le cosiddette librerie) e di concatenare le elaborazioni nel tempo come in una partitura, seguendo regole complesse. In questo modo il calcolatore abolisce le estenuanti e irreversibili fasi di montaggio dei nastri basate sul collage e sul missaggio di numerosi e brevi frammenti ottenuti da elaborazioni analogiche, permettendo revisioni e pentimenti.
Negli anni Sessanta il rinnovato interesse per le esecuzioni dal vivo pone la ‘questione del tempo reale’ come problema estetico dai notevoli risvolti tecnologici. Un interesse che porterà allo studio di algoritmi specifici per l’audio e la musica, e alla ricerca di diversi modi per superare i limiti di velocità dei primi calcolatori elettronici numerici.
I sistemi numerici a tempo campionato e i sistemi continui
Il trasferimento nei sistemi numerici dei circuiti e dei procedimenti dell’elettronica analogica −la loro trasformazione in algoritmi − è oggetto dell’elaborazione numerica del segnale, una disciplina trasversale a diversi domini applicativi cui dobbiamo inoltre procedimenti impensabili (o irrealizzabili) nel mondo analogico, quali la trasformazione e antitrasformazione di Fourier o i filtri senza distorsione di fase (filtri FIR).
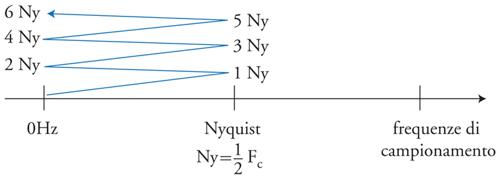
Il calcolatore numerico opera in tempo e in ampiezze discreti. Il teorema del campionamento stabilisce infatti che in tempo discreto è possibile rappresentare solo segnali con un dominio di frequenza compatto. Se per esempio il tempo di campionamento è costante (il suo inverso è la frequenza di campionamento, sampling frequency o sampling rate), non sono rappresentabili frequenze superiori alla frequenza di Nyquist, pari alla metà di quella di campionamento. Frequenze superiori generate o introdotte nel sistema vengono ripiegate ‘a soffietto’ in posizioni rappresentabili, dando luogo alle cosiddette frequenze fantasma. Il fenomeno, assente nei sistemi analogici, è detto foldover o aliasing (fig. 3).
Le frequenze fantasma vengono riprodotte dalla riconversione in analogico nella posizione ripiegata, producendo una distorsione della composizione spettrale alla quale il nostro sistema uditivo è particolarmente sensibile.
L’uso dei sistemi numerici porta dunque con sé, rispet-to allo strumentario analogico, una serie di possibilitànuove ma anche di problemi specifici. La limitazione di banda dei sistemi campionati è anche responsabile di una progressiva compressione dell’asse delle frequenze nelle vicinanze della frequenza di Nyquist, compensabile solo in modo approssimato. Le caratteristiche spettrali e di fase dei filtri lineari numerici possono quindi solo approssimare quelle delle loro controparti analogiche.
La discretizzazione delle ampiezze produce altri fenomeni indesiderati quali il rumore di quantizzazione, dovuto alla granularità introdotta dalla riduzione all’intero dell’ampiezza e particolarmente fastidioso dal punto di vista uditivo.
Per interfacciare i sistemi numerici a quelli analogici si utilizzano specifici circuiti: i convertitori analogico-digitali (ADC) e digitale-analogici (DAC). Un ADC trasforma un segnale analogico in tensione in una sequenza di interi binari con un determinato numero di bit (inizialmente 4, poi 8, 10, 12, 14, 16, 20 e oggi 24). Un DAC trasforma, al contrario, un numero binario in una tensione analogica. Poiché il semplice campionamento di un segnale analogico produrrebbe foldover, i convertitori audio (a differenza di quelli usati nei sistemi di controllo) sono processori numerici che utilizzano il sovracampionamento e il filtraggio numerico. Anche il rumore numerico è sfumato (noise dithering) mediante mascheramento con rumore bianco per renderlo meno sgradevole.
Gli algoritmi della computer music
Anche nel campo della computer music si presenta la problematica del rapporto continuo-discreto. Molti procedimenti analogici vengono replicati con guadagno di precisione e qualità sonora, ma le tecniche di modulazione (tutte allargano la banda) possono produrre aliasing e richiedono diverse precauzioni. La modulazione ad anello, per esempio, produce segnali virtualmente a banda infinita e, se implementata verbatim in un sistema numerico, oltre all’aliasing produce il ronzio fastidioso alla frequenza della modulante già presente nei circuiti analogici basati su componenti a larga banda.
In compenso, si sono resi disponibili procedimenti specificamente numerici: la modulazione di frequenza, una delle prime applicazioni della computer music in tempo reale, ma anche tecniche nel dominio della frequenza (basate sulle trasformate e antitrasformate di Fourier), sofisticate distorsioni non lineari, pitch-shift e time stretch con meno artefatti, inseguitori di intonazione e di inviluppo più affidabili.
Oscillatori numerici
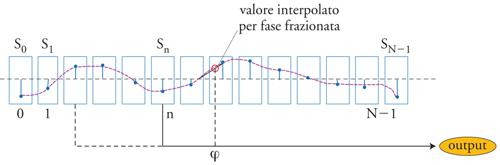
L’algoritmo più utilizzato per implementare un oscillatore numerico consiste in una tabella di valori (campioni della forma d’onda desiderata) memorizzati in un buffer di memoria e letti in modo circolare al ritmo della frequenza di campionamento (fig. 4).
Una forma di interpolazione (in genere lineare) tra un valore e l’altro permette frequenze di scansione non limitate ai soli sottomultipli della frequenza di campionamento, una grana troppo grossa per le esigenze di intonazione musicale (è questo il problema dell’intonazione, legato all’uso di fasi intere). L’interpolazione richiede un’efficiente rappresentazione dei numeri frazionari, per la quale si adotta oggi la virgola mobile (floating point). L’interpolazione lineare introduce inoltre foldover (una spezzata non è infatti a banda limitata), che può essere reso trascurabile utilizzando un numero di punti sufficientemente alto (tipicamente 512 per forme d’onda sinusoidali).
Un oscillatore tabellare interpolato permette dunque di generare forme d’onda periodiche qualsiasi, ovvero note musicali. Esso non è altro che la realizzazione numerica di un procedimento analogico ben noto. Si tratta della boucle già utilizzata nell’immediato secondo dopoguerra nel laboratorio di Pierre Schaeffer presso la ORTF a Parigi e consistente in un solco chiuso di un disco grammofonico (oppure di un anello chiuso di nastro magnetico) letto a velocità variabile.
La modulazione di frequenza (FM). - Uno dei centri statunitensi più attivi nella nascente computer music degli anni Sessanta è il CCRMA (Center for computer research in music and acoustics) dell’Università di Stanford, dove nel 1967 John Chowning mette a punto (e brevetta) l’algoritmo di sintesi a modulazione di frequenza (FM), ispirato alle omonime tecniche di radiotrasmissione.
L’espressione della modulazione di frequenza è la seguente:
[1] sFM(t) =sen[∫t0 (ωP+AFM sen(ωM τ))dτ].
Lo spettro del segnale modulato è composto dalla pulsazione della portante ωP più un pettine equispaziato, simmetrico, centrato attorno a essa con passo ωM: ωn=ωP±m∙ωM, con m=0,1,…∞. L’indice m, detto ordine, (ordine) designa una coppia di righe simmetriche attorno alla portante.
La sintesi FM permette con due soli oscillatori di produrre suoni composti virtualmente di infinite parziali ed è quindi particolarmente adatta agli hardware numerici poco potenti dell’epoca.
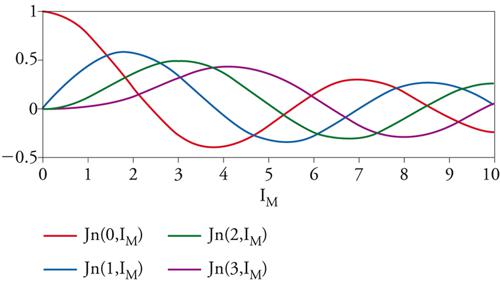
Le ampiezze sono governate dalle funzioni di Bessel di prima specie: Am=Jn(m,IM), dove Im=AFM/ωM è detto indice di modulazione. Lo spettro è praticamente limitato in frequenza: per la natura del tratto iniziale delle funzioni di Bessel, ordini superiori a mmax≈IM+4,3 hanno ampiezza trascurabile. Se l’indice di modulazione controlla in modo semplice la larghezza di banda, non così si può dire per le ampiezze dei singoli ordini che, a causa della natura oscillante delle funzioni di Bessel, seguono invece andamenti complicati (fig. 5).
La FM si guadagnerà così la fama di essere potente ma complessa.
Nel 1980 la Yamaha ha acquisito i diritti del brevetto e realizzato la serie DX di tastiere FM: i primi sintetizzatori numerici in tempo reale disponibili sul mercato, che hanno dato il via all’era degli strumenti musicali numerici come prodotto di massa.
Convoluzione e morphing. - La risposta a un segnale qualunque dei sistemi lineari invarianti nel tempo e rappresentabili con una funzione di trasferimento è ottenibile come convoluzione del segnale in ingresso per la risposta all’impulso del sistema, operazione che nel dominio della frequenza corrisponde al prodotto delle trasformate dei due segnali. Nella musica elettronica la convoluzione di due segnali (anziché di un segnale e di una risposta all’impulso) permette di ottenerne uno il cui spettro è il prodotto degli spettri, che quindi ha caratteristiche miste, ibride tra i due, e permette un morphing graduale tra l’uno e l’altro.
Analisi e sintesi additive. - La combinazione lineare di oscillatori sinusoidali può a prima vista apparire il metodo di sintesi più semplice e immediato, ma è in realtà gravato da una duplice difficoltà. Da una parte richiede una potenza di calcolo notevole, almeno se si vogliono sintetizzare suoni spettralmente densi (come quelli degli strumenti acustici e degli ensemble). Dall’altra implica la manipolazione di un alto numero di parametri (frequenza, ampiezza e talvolta anche fase iniziale di ogni oscillatore), circostanza che richiede una conoscenza approfondita del significato percettivo di ogni singolo dato e della sua evoluzione temporale che a tutt’oggi si possiede solo in forma rudimentale.
Nonostante queste indubbie difficoltà, le potenze di calcolo oggi disponibili ci permettono di guardare a entrambi i problemi in modo molto diverso rispetto alla fine del Novecento. Sono effettivamente utilizzabili strumenti e metodi di analisi basati su FFT (Fast Fourier transform, algoritmo introdotto nel 1965 da James W. Cooley e John W. Tukey) in grado di individuare i picchi spettrali per frame temporali brevi (decine di millisecondi). L’analisi sinusoidale (R. J. McAulay e Thomas F. Quatieri) ne opera una potatura riducendo il numero di oscillatori necessari alla resintesi. Ogni frame temporale è descritto così da una matrice di coppie ampiezza-frequenza in grado di approssimare percettivamente il segnale analizzato. La quantità di informazione da trasmettere viene ridotta (compressione) ed è possibile cambiare le ampiezze e le frequenze tra analisi e resintesi. Modificando per esempio le frequenze in modo proporzionale si ottiene un pitch-shift, con leggi diverse si altera l’armonicità e il timbro, mentre con lunghezza del frame differenti dall’originale si ottiene un time-stretch. Gli odierni (2008) calcolatori da tavolo permettono di generare in tempo reale almeno un migliaio di oscillatori sinusoidali, mentre sistemi specifici ad alto parallelismo possono raggiungere i centomila oscillatori.
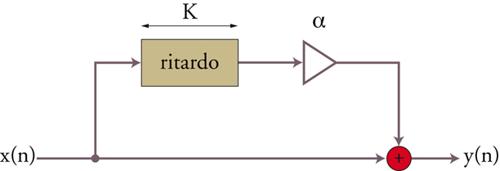
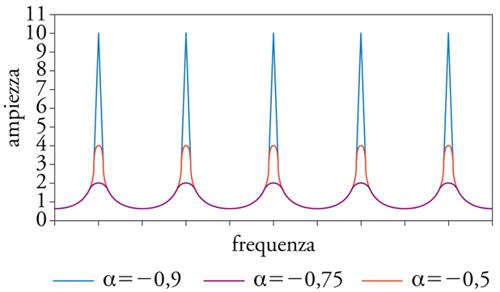
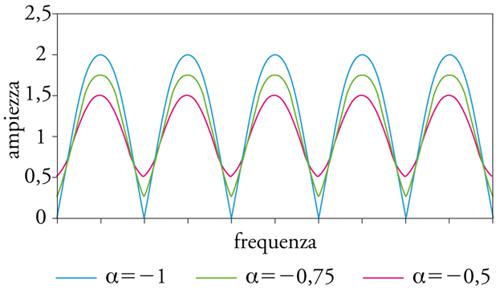
Filtri comb. - Nei sistemi numerici sono facilmente implementabili i filtri a pettine (comb), pressoché irrealizzabili in elettronica analogica in campo audio perché richiedono linee di ritardo con tempi macroscopici. Nel filtro a pettine diretto (feedforward) l’uscita della linea di ritardo viene miscelata al segnale d’ingresso; nel tipo a controreazione (feedback) viene invece rinviata al suo stesso ingresso miscelata al segnale d’ingresso.
Uscita e ingresso della linea di ritardo interferiscono costruttivamente o distruttivamente se il periodo della componente del segnale è un multiplo rispettivamente intero o semintero del tempo di ritardo della linea. Un filtro a pettine presenta dunque un andamento periodico nello spettro, con enfasi o deenfasi a frequenze multiple di quella corrispondente al periodo di ritardo (fig. 6 A, B, C, D).
I filtri comb si prestano dunque alla generazione di suoni intonati o a simulare le interferenze dovute a riflessioni multiple in ambienti chiusi.
Il protocollo MIDI per l’interconnessione di strumenti elettronici. - Lo standard MIDI (Musical instrument digital interface) definisce un protocollo seriale asincrono con 8 bit di dati senza parità a 31.250 bit/sec, che ha lo scopo di permettere l’interconnessione di dispositivi musicali numerici. I messaggi MIDI sono di tre o più byte, dei quali il bit più significativo è utilizzato per designare l’inizio sequenza riducendo a 7 quelli utili.
Le informazioni trasmesse sono codici di nota e valori di controlli (volumi, intensità, intonazione, pedali ecc.). La nota è codificata con 7 bit (0÷127), del tutto sufficienti allo scopo tenendo conto che un moderno pianoforte da concerto è dotato di 80 tasti.
Premendo uno dei tasti, una tastiera MIDI genera il messaggio seguente:
Status byte (note-on) Note Velocity
STATUS BYTE: il bit più significativo è a uno per indicare l’inizio sequenza. I quattro bit meno significativi codificano il cosiddetto canale MIDI (0÷15) al quale il messaggio appartiene. I tre bit immediatamente più significativi codificano l’evento (0÷8). Il NOTE-ON (pressione di un tasto) ha codice 1.
NOTE: codice di nota in 7 bit (0÷127). Il bit più significativo è a zero.
VELOCITY: velocità di caduta del tasto (forza della percussione), sempre in 7 bit (0÷127). Il bit più significativo è a zero.
La codifica dei 16 canali MIDI permette di smistare i messaggi in una rete tra apparecchiature diverse, perché è possibile istruire i dispositivi MIDI stessi a trasmettere su un determinato canale e ad ascoltare solo uno specifico gruppo di canali.
Altri messaggi permettono di trasmettere lo stato di controlli (slitte, potenziometri, pedali ecc.) per selezionare diversi parametri nel sintetizzatore.
Nella struttura dei messaggi traspare chiaramente la tastiera come paradigma di interfaccia, associata a meccanismi di sintesi basati su note e scale. La velocità di trasmissione, anche se del tutto adeguata a tastiere con elevata polifonia e molti controlli, appare oggi insufficiente per trasmettere informazioni più complesse.
Nonostante questi limiti, tale tecnologia sopravvive fino ai nostri giorni grazie alla disponibilità sul mercato di tastiere, mixer, pedali, joystick e così via dotati di interfacce MIDI. Tutti gli odierni programmi per la musica consentono un trattamento algoritmico dei messaggi MIDI, riuscendo in questo modo a piegarli a usi diversi da quelli originali.
Il riverbero artificiale e la spazializzazione. - Dal secondo dopoguerra i compositori desiderano comporre anche il cosiddetto spazio d’ascolto, utilizzando il movimento delle sorgenti come un elemento di contrappunto (per es., per fondere o distinguere due voci). Oltre che auralizzato il suono deve essere quindi spazializzato, cosa che richiede sistemi oggi solo parzialmente disponibili.
Nell’approccio più immediato, una spazializzazione a diversi canali con altoparlanti tradizionali avviene dosando le ampiezze in funzione dell’angolo di provenienza che si vuole sia percepito. Un suono bilanciato sul-l’orecchio destro e sinistro, ma proveniente da due sorgenti diverse, non stimola tuttavia il sistema uditivo esattamente come un suono proveniente da davanti. Il bilanciamento interaurale dipende inoltre non solo da quello dei canali, ma anche dalla posizione relativa tra ascoltatore e diffusori. È inoltre impossibile realizzarein questo modo attraversamenti della platea o sollevare l’azimut percepito rispetto al piano definito dagli altoparlanti. In sale chiuse, il riverbero può alterare il bilanciamento dei canali cancellando le intenzioni esecutive. Dato che il riverbero è funzione dell’occupazione della sala, anche una calibrazione eseguita a sala necessariamente vuota può risultare illusoria.
A questi inconvenienti si cerca di fare fronte utilizzando criteri psicoacustici ulteriori rispetto alle sole intensità: simulazioni di ITDA (Interaural time difference of arrival, un ulteriore meccanismo sottostante alla nostra percezione della direzione di arrivo); filtraggi basati sulle HRTF (Head related transfer functions) per simulare l’individuazione della direzione di arrivo effettuata dal filtro variabile della testa e dei padiglioni auricolari, meccanismo responsabile della risoluzione dell’ambiguità avanti-dietro e alto-basso; modifica del rapporto tra suono diretto e suono riverberato per modulare la sensazione di distanza, utilizzando riverberi artificiali. Un’esigenza stringente (e ancora sostanzialmente inevasa) è quella di avere diffusori fortemente direttivi per rendere indipendenti i criteri direzionali dalla collocazione fisica dell’ascoltatore e dal riverbero naturale.
Questi sono solo brevi cenni delle numerose difficoltà che si incontrano nella concezione e messa in funzione di sistemi di spazializzazione per esigenze espressive. Assai diversi sono i sistemi commerciali per sale cinematografiche, che si pongono obiettivi più limitati e fanno riferimento ad ambienti appositamente concepiti dove è presente solo suono riprodotto.
La musica di sintesi è di per sé anecoica, una caratteristica timbrica poco desiderabile soprattutto quando i suoni, a causa dei mezzi limitati, erano spettralmente poveri. Anche la musica strumentale registrata in studio presenta caratteristiche anecoiche non desiderabili. Il riverbero artificiale riveste dunque una notevole importanza sia nella spazializzazione sia nelle attività cosiddette di post-elaborazione negli studi di registrazione.
I primi riverberi artificiali erano basati su stanze ecoiche isolate acusticamente dall’ambiente esterno, una soluzione costosa, ingombrante e rigida che rendeva difficile variare i tempi di riverbero. Sono stati in seguito introdotti ingegnosi sistemi basati sulla propagazione del suono nei metalli (piastre e molle), cercando di ottenere basse velocità di propagazione in modo da imitare in poco spazio un volume ampio. Un’approssimazione del riverbero si otteneva nella tape music con magnetofoni dotati di testine di riproduzione multiple e sfalsate, o miscelando copie di frammenti sfalsate temporalmente.
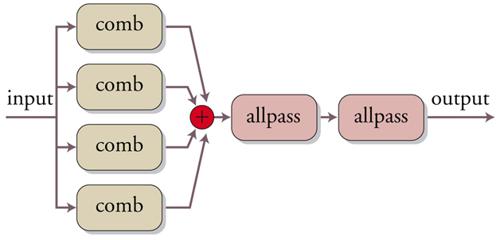
La computer music rende disponibili diversi algoritmi di simulazione, con sostanziali miglioramenti qualitativi. Il primo è dovuto a Manfred R. Schroeder e si basa su di una prima sezione composta di filtri comb di lunghezza opportuna, in modo da introdurre un’eco con un decadimento esponenziale, imitando così le prime riflessioni sulle pareti, mentre una seconda sezione di filtri passa-tutto genera una coda di decadimento più confusa sfruttando le caratteristiche dispersive del filtro che simulano riflessioni diffusive (fig. 7).
In seguito, con l’aumento delle potenze di calcolo, sono stati introdotti riverberi a modello fisico, basati sulla convoluzione con una funzione di trasferimento misurata da una sala reale oppure sintetizzata mediante modelli di propagazione. Questa linea di ricerca è ancora aperta e densa di proposte.
Le macchine numeriche specializzate
Negli anni Settanta le potenze di calcolo dei dispositivi programmabili per uso generale erano ancora insufficienti per la generazione del suono in tempo reale. Fu dunque necessario realizzare dispositivi numerici specializzati che superassero i limiti di quanto il mercato offriva in quel momento.
La 4X all’IRCAM di Parigi
Nel 1975 al neonato IRCAM (Institut de Recherche et Coordination Acoustique/Musique) di Parigi, Pierre Boulez e Luciano Berio chiamano Giuseppe di Giugno, un fisico italiano che aveva creato all’Università di Napoli un Centro di ricerca per l’elettroacustica e l’audio digitale.
Di Giugno realizza all’IRCAM diversi prototipi di sistemi numerici cablati che sfociano nel 1979 nella 4X, la prima stazione di lavoro musicale interamente digitale per la sintesi e l’analisi del suono in tempo reale, dotata di una velocità di calcolo corrispondente a circa 200 personal computer dell’epoca. La 4X sarà utilizzata da Berio, Boulez e Stockhausen ma anche dai compositori borsisti che l’IRCAM ospiterà negli anni seguenti.
Il Digital signal processor (DSP)
Dopo gli anni Ottanta per l’elaborazione numerica del segnale si afferma l’uso del DSP (Digital signal processor): un processore programmabile specificamente ottimizzato per compiti quali il calcolo di filtri e l’analisi FFT. Dalla fine degli anni Ottanta in poi molti DSP verranno dotati anche di dispositivi di comunicazione veloci che ne faranno dei Transputer, collegabili in diverse topologie per il calcolo parallelo SIMD (Single instruction multiple data) e MIMD (Multiple instruction multiple data). Queste caratteristiche permetteranno un uso effettivo dei DSP per la musica in tempo reale, con minori tempi e costi di sviluppo e notevoli vantaggi di flessibilità rispetto ai dispositivi puramente hardware.
I sistemi IRCAM basati su Next-Step
L’IRCAM abbandonerà dunque la filosofia della 4X, introducendo nello sviluppo dei suoi sistemi il DSP sotto forma di sottosistemi specializzati ospitati in macchine general purpose, quali all’inizio il Next. Si trattava di una macchina con sistema operativo derivato da Unix, di potenza di calcolo insufficiente ma che montava al suo interno il DSP MOTOROLA 56000 ad aritmetica in virgola fissa per l’elaborazione del suono. In seguito, a causa del limitato successo commerciale del Next che ne decreterà rapidamente la scomparsa, l’IRCAM si è rivolta a piattaforme commerciali quali Apple e Microsoft, abbandonando l’uso di hardware specializzati e convertendosi alla software music.
Altri sistemi basati su DSP
A Roma, nei primi anni Ottanta, il Centro ricerche musicali − uno studio gravitante attorno ai due compositori Michelangelo Lupone e Laura Bianchini − mette a punto prima il Fly 10, basato sul DSP Texas Instruments C10 in virgola fissa e ospitato in un personal computer Apple, e poi nel 1990 il Fly 30, basato su PC IBM e DSP TI C30 in virgola mobile.
Nel 1994 si afferma commercialmente il sistema KYMA-CAPIBARA, basato su un box con 8 DSP MOTOROLA 56000 (CAPIBARA) e collegato a un computer Apple MacIntosh dotato di software specializzato per la sintesi e l’elaborazione in tempo reale (KYMA).
I sintetizzatori commerciali odierni a campionamento (wavetable)
Gli strumenti musicali elettronici odierni (tastiere) perseguono intenti solo imitativi nel tentativo di fornire a un unico esecutore, attraverso un unico strumento e un’unica interfaccia, la possibilità di simulare un gran numero (centinaia) di diversi strumenti solisti o ensemble strumentali. Automatismi esecutivi quali accompagnamenti ritmici e armonizzazioni secondo predefiniti stilemi di genere (pop, rock, jazz ecc.) o anche dispositivi in grado di rettificare l’imperfetta intonazione di un cantante forniscono ulteriori supporti a questa ‘one man orchestra’.
Il meccanismo di sintesi utilizzato è quello a wavetables o a campionamento, che consiste nell’inviare all’uscita audio, a comando del tasto, una registrazione numerica della nota di uno strumento previamente memorizzata. Apparso sul mercato negli anni Settanta con il Fairlight CMI (Computer musical instrument), questo meccanismo deriva dall’implementazione numerica di idee piuttosto datate: ancora una volta la boucle di Schaeffer e il suo successivo perfezionamento nel Phonogène, basato su un anello di nastro la cui velocità era controllata da una tastiera.
Un campionatore permette di memorizzare suoni (i cosiddetti campioni) e successivamente di eseguirli a comando di tastiere o sotto il controllo di un programma.
Perché l’ascolto fornisca anche solo una somiglianza con un’esecuzione musicale è però necessaria più di un’accortezza. L’intensità del suono deve per esempio essere correlata alla velocità con la quale il tasto viene percosso, effetto ottenuto modulando l’inviluppo di ampiezza. La durata di un suono registrato poi è limitata mentre è spesso l’esecutore che determina la durata di una nota. A questo scopo, nella coda del campione viene individuata una zona adatta a essere riprodotta in anello (loop) per prolungarlo a piacere.
Per permettere l’esecuzione di glissati e consentire l’intonazione dello strumento in un ensemble (oltre che per risparmiare memoria), un meccanismo di pitch-shift permette di ottenere qualsiasi intonazione a partire solo da un ridotto numero di campioni a intonazioni diverse. Il pitch-shift è utilizzato anche per la correzione di intonazione di cantanti stonati.
Nonostante i numerosi perfezionamenti, le capacità imitative fornite da questo approccio continuano a soffrire di diversi inconvenienti, alcuni dei quali di principio e pertanto irrimediabili.
L’anello finale introduce in coda una periodicità che conferisce al suono un carattere artificiale, a meno di non adottare anelli lunghi molti secondi al costo di memorie di maggiori dimensioni. L’intensità del suono emesso negli strumenti musicali in funzione del gesto esecutivo non equivale solo a un cambiamento di inviluppo di ampiezza ma per esempio cambiano anche, e in modo complesso, gli inviluppi delle singole parziali. Se i suoni sono stati registrati a un’intensità media, il pianissimo e il fortissimo risulteranno innaturali e più che di una diversa dinamica si avrà l’impressione di uno strumento ascoltato da lontano o da vicino.
Gli inconvenienti più significativi sono però dovuti al problema dell’interfaccia: le tastiere, le slitte, i potenziometri e così via, non permettono all’esecutore di replicare quelle delicate interazioni con lo strumento fisico responsabili delle sfumature che distinguono un’esecuzione meccanica, scolastica, da una di qualità artistica. Sfumature che, per di più, il sintetizzatore non sarebbe in grado di riprodurre ma delle quali qualunque strumentista appena decente fa ampio e consapevole uso.
Questi limiti sono particolarmente evidenti nell’imitazione di strumenti quali fiati e archi, che permettono una maggiore varietà di emissione del suono e di prosodia tanto nei singoli suoni (articolazione) quanto nel raccordo tra suoni adiacenti (fraseggio).
Tentare di imitare uno strumento esistente è inoltre un evidente nonsense musicale: l’originale è sempre migliore della copia e inoltre permette una scoperta continua di nuove modalità d’uso, come frequentemente accade in tutta la musica contemporanea.
L’avvento del personal computer
La legge di Moore − che prevede il raddoppio della potenza di calcolo dei dispositivi numerici ogni due anni a prezzi e ingombri quasi costanti − trasforma a partire dalla fine degli anni Settanta i calcolatori per usi generali in prodotti di consumo, mettendo almeno nominalmente a disposizione dell’utente domestico e generalista potenze di calcolo del tutto ragguardevoli.
Col passaggio dai sistemi hardware o DSP, dedicati o ibridi, alle macchine di consumo, la computer music si tramuta in software music. Emergono nuovi problemi dovuti essenzialmente ai sistemi operativi, oggi tutti basati sullo schema prehemptive multitasking, adatto a usi generali e a una interazione amichevole con l’utente ma inadeguato al tempo reale.
È difficile, se non impossibile, ottenere in questi contesti latenze audio brevi e predicibili in modo accettabile; per non parlare del tempo reale propriamente detto, che richiederebbe latenze deterministiche di un solo campione (talvolta indispensabile in campo audio). I sistemi a bassa latenza attuali non scendono significativamente sotto i 10 msec, pari al periodo di una sinusoide di solo 1 KHz. Un sintetizzatore dovrebbe avere inoltre tempi di risposta comparabili con il timing di un musicista esecutore, piuttosto stretto.
Si sono comunque diffusi programmi per l’elaborazione del segnale musicale per i personal computer, destinati a un uso generale − non specificamente legati a un’estetica o a una tecnica di elaborazione o sintesi determinate − o specializzati per estetiche o tecniche precise.
Tra i programmi generali, un primo gruppo fa uso della programmazione a data flow fornendo in video un sistema di patching di algoritmi. Tra questi: (a) MAX-MSP, un software proprietario per Windows e MacOS; (b) Pure Data, dovuto a Miller Puckette, una versione successiva e open source di MAX-MSP con il quale ha una certa compatibilità; (c) CPS, di recente divenuto freeware, per Windows e MacOS.
Un secondo gruppo adotta il paradigma del linguaggio di programmazione. Oltre al già citato c-sound, SuperCollider, per Linux, Windows e MacOS, basato su di un linguaggio dinamico e su una architettura client-server.
Tra i pacchetti non generali ricordiamo: (a) i GRM-Tools (del GRM di Radio France, il gruppo che fu di Schaeffer), orientati alla musica spettrale; (b) AudioSculpt (dell’IRCAM), basato su di un supervocoder per l’analisi e resintesi additiva; (c) Pulsar (del compositore statunitense Curtis Roads), per la sintesi granulare secondo paradigmi stilistici tipici dell’autore.
La sintesi per modelli fisici
Attorno agli anni Ottanta la comunità dei ricercatori musicali intravede la possibilità di ottenere suoni senza sintetizzare segnali. Dopotutto uno strumento musicale acustico è un oggetto fisico vibrante, della cui dinamica è possibile concepire un modello fisico-matematico basato su equazioni differenziali del moto. La loro soluzione in tempo reale permetterebbe di fare ‘suonare’ il modello simulando l’oggetto fisico. Questo nuovo capitolo prese subito il nome di sintesi per modelli fisici.
Karplus-Strong
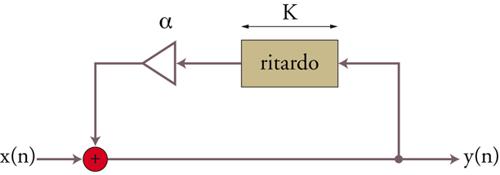
Nel 1983 al CCRMA di Stanford due studenti, Kevin Karplus e Alex Strong, gettano uno sguardo diverso sull’oscillatore tabellare pensandolo come una memoria automodificabile. Lo schema con il quale si rappresenta l’algoritmo è raffigurato in fig. 8. Il movimento di dati suggerito dalle frecce è solo virtuale, ed è in realtà implementato con un puntatore che viene aggiornato; ciascun dato viene letto e poi riscritto nella medesima posizione dopo la moltiplicazione per il fattore G. Caricando nella tabella una forma d’onda, se G〈1 questa si attenuerà progressivamente in modo esponenziale, come accade per una corda pizzicata.
Con questo semplice algoritmo è dunque possibile ottenere suoni plausibili con spettri complessi ma per un uso musicale effettivo deve essere risolto il problema dell’intonazione, già incontrato negli oscillatori tabellari. L’algoritmo può inoltre suonare solo condizioni iniziali, in maniera analoga a quanto avviene con un plettro ma non con un martello o con l’archetto.
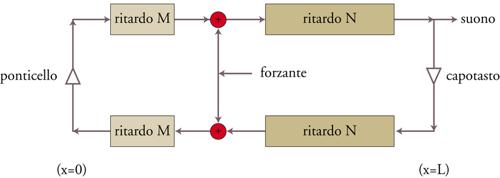
Le guide d’onda (waveguides)
A Julius Orion Smith III, sempre al CCRMA, si deve l’evoluzione dell’algoritmo di Karplus e Strong nelle cosiddette guide d’onda numeriche.
L’equazione conservativa di una guida d’onda monodimensionale (una corda ne è un esempio) ammette le soluzioni di d’Alembert
[2] y(x, 0) = y0(x) y(x, t) = y0(x + c∙t) + y0(x − c∙t)
che descrivono il moto libero come sovrapposizione di due onde che propagano le condizioni iniziali nei due versi.
Se esistono vincoli sulle estremità, per esempio (y(0,t) =y(L,t)=0, queste vi si riflettono con inversione di segno. Una guida d’onda numerica può quindi essere rappresentata come nella fig. 9.
Il modello permette di introdurre una forzante in un punto della guida, esprimendo correttamente la sua influenza sull’evoluzione del moto. È dunque possibile prendere in considerazione eccitazioni (martelli, archetti) e non solo condizioni iniziali.
Il problema dell’intonazione può essere risolto con l’introduzione di ritardi frazionari a una delle estremità, che non possono però essere calcolati con un’interpolazione lineare ma richiedono un’interpolazione a banda limitata − costosa in termini di calcolo − o almeno una sua approssimazione accettabile musicalmente. Al contrario dell’oscillatore interpolato, la lunghezza qui non è arbitraria ma determinata dal rapporto tra intonazione e frequenza di campionamento, cosa che conduce a guide piuttosto corte, con l’eccezione delle note gravi.
Nel caso delle corde, il decadimento esponenziale ottenuto con un’attenuazione all’estremità non è realistico: in realtà il contributo al moto delle parziali alte decade più rapidamente e in maniera più accentuata per le corde di budello o nylon rispetto a quelle di metallo. Un comportamento del genere può essere approssimato introducendo un filtro passa-basso al posto di un’attenuazione fissa. Questi e altri indispensabili raffinamenti fanno crescere la complessità di calcolo e impongono un equilibrio piuttosto delicato tra precisione e tempo di calcolo.
La Yamaha ha prematuramente commercializzato nel 1995 la tastiera VL-1 basata su modelli fisici, senza nessun successo né musicale né commerciale a causa della grossolanità dei risultati sonori.
I metodi finitistici e modali
CORDIS-ANIMA di Claude Cadoz, Annie Luciani e Jean-Loup Florens (1993) si basa sulla modellizzazione degli oggetti vibranti per mezzo di elementi concentrati quali masse puntuali, molle e smorzatori viscosi. Un approccio modulare permette all’utente di interconnettere gli oggetti elementari in modo da costruire liberamente il proprio strumento virtuale. Il metodo si presta male al tempo reale e i programmi che lo utilizzano si limitano a un esiguo numero di parziali a causa della complessità di calcolo. Questa è proporzionale a N(n+1), dove N è il numero di parziali desiderato e n è il numero di dimensioni spaziali dell’oggetto.
Sulla sintesi modale, nella quale il moto vibratorio è espresso come sovrapposizione di modi, si fonda invece MODALYS (derivato dal Mosaic di Jean-Marie Adrien e Joseph Derek Morrison, 1993). Esso richiede la formulazione delle relazioni che legano le eccitazioni ai singoli modi e le matrici di interazione tra le varie componenti.
Anche qui i calcoli crescono con il numero di modi con una legge di potenza e il metodo si presta male al tempo reale. In compenso può usufruire di un’ampia mole di metodiche analitiche e sperimentali tratte dalla vibroacustica industriale, nella quale l’analisi modale è utilizzata per model-lare il comportamento vibratorio di elementi strutturali di macchinari, edifici, strutture, parti di aerei e altri mezzi di trasporto.
Metodi diretti
Un ulteriore e più recente approccio consiste nell’integrare direttamente il moto di tutta la corda a partire da una sua espressione continua nello spazio, utilizzando metodi alle differenze finite per l’integrazione nel tempo. L’algoritmo ha permesso di ottenere in differita risultati musicalmente significativi, che sono stati utilizzati per la composizione di Corda di metallo per quartetto d’archi e nastro magnetico (Kronos Quartet, Roma, 1998) e Canto di Madre per supporto digitale (Radio Vaticana, 1999) di Michelangelo Lupone.
Uno sguardo a un futuro possibile
Nuovi hardware e sistemi
Attualmente i DSP sono utilizzati in prodotti di largo consumo come i telefoni cellulari, i lettori MP3, i videotelefoni e i computer palmari. Nelle applicazioni di punta sono stati rimpiazzati dalla tecnologia FPGA (Field programmable gate array), matrici di porte logiche liberamente interconnettibili sul campo semplicemente scrivendo una memoria riutilizzabile. Con le FPGA anche la costruzione di un circuito su silicio prende una forma software, con librerie di sottosistemi sotto forma di macro da interconnettere a un livello più alto. Si realizzano in questo modo dispositivi ad hoc veloci dotati di alto parallelismo per il calcolo vettoriale, ormai chiaramente risolutivo per la gran parte delle applicazioni di calcolo numerico intensivo, inclusa l’elaborazione del segnale musicale.
Sul fronte dei videogiochi, famelici di risorse di calcolo per animazioni 3D ed effetti sonori, l’industria utilizza oggi hardware e sistemi operativi dedicati. La Playstation 3 della Sony adotta il cell computer IBM, un sistem-on-chip dotato di molte unità vettoriali in floating point con una potenza di calcolo pari a un paio di centinaia di Pentium, avvicinandosi al TeraFlop/sec.
Oltre il MIDI: OSC (Open sound control)
Per superare i limiti tecnologici e concettuali del MIDI è in via di consolidamento OSC, un protocollo trasportabile su diversi strati fisici e logici (Ethernet, UDP ecc.) che permette di scambiare, tra computer, sintetizzatori e dispositivi multimediali dati ad alta risoluzione, anche in virgola mobile, strutturati in pacchetti.
Streaming di dati di analisi e di sintesi: SDIF
Per la memorizzazione e lo streaming audio è oggi in via di sviluppo e consolidamento SDIF: un protocollo aperto che permette l’implementazione di diversi formati oltre al PCM. SDIF può trasportare dati per sintesi additiva da analisi a vocoder o sinusoidale, dati di inseguimento di intonazione, tracciamento di formanti e così via.
La fine di un’era?
«Da alcuni anni la musica elettronica fa meno rumore, se ne parla sempre meno ed è raro incontrare musicisti e pubblicisti che ne parlino ancora col vocabolario avveniristico e ottimista degli anni Cinquanta e che l’assumano come vessillo avanguardista o come simbolo di liberazione dalla schiavitù dell’accademia strumentale. […] La musica elettronica in un certo senso ‘non esiste’ più perché è dappertutto e fa parte del pensare musicale di tutti i giorni». Con queste parole nel 1976 il compositore Luciano Berio sanciva la maturità artistica della musica elettronica e l’ingresso della tecnologia elettronica nel bagaglio intellettuale del compositore-artista contemporaneo.
Se oggi gettiamo uno sguardo all’indietro, osserviamo però che quasi tutto ciò che è stato inventato nella musica elettronica risale proprio a quella fase pionieristica. Ciò che ne è seguito è stato da una parte un mero perfezionamento delle applicazioni di quelle idee e dall’altra il loro più o meno riuscito sfruttamento commerciale. A distanza di trent’anni l’industria degli strumenti musicali si è ripiegata su sé stessa e non sembra più in grado di recepire o di stimolare soluzioni nuove, scollandosi dal pensiero musicale artistico. Un certo isolamento reciproco è riscontrabile anche tra ricerca e pensiero musicali: la prima tentata dalla lusinga di precoci applicazioni commerciali, in un malsano rapporto utilitaristico − spesso solo tentato − con l’industria; il secondo alla difficile ricerca di nuovi stimoli e di nuovi rapporti con una scienza e una tecnologia sempre più risucchiate da un mainstream che lascia poco spazio ad apporti originali. Non è difficile riconoscere in questi tratti un comune profilo del nostro tempo, nel quale la prospettiva si è contratta attorno a un presente dominato dalla sola ricerca di risultati a breve termine.
Bibliografia
Cingolani, Spagnolo 2005: Acustica musicale e architettonica, a cura di Sergio Cingolani, Renato Spagnolo, Torino, UTET, 2005.
De Poli 1991: Representations of musical signals, edited by Giovanni De Poli, Aldo Piccialli, Curtis Roads, Cambridge (Mass.), MIT Press, 1991.
Dodge, Jerse 1997: Dodge, Charles - Jerse, Thomas A., Computer music: synthesis, composition, and performance, 2. ed., New York, Schirmer, 1997.
Dunn 1992: Dunn, David, A history of electronic music pioneers, open document.
http://www.davidddunn.com/~david/writings/pioneers.pdf.
Galante, Sani 2000: Galante, Francesco - Sani, Nicola, Musica espansa. Percorsi elettroacustici di fine millennio, Milano, Ricordi-MBG, 2000.
Karplus, Strong 1983: Karplus, Kevin - Strong, Alex, Digital synthesis of plucked string and drum timbres, “Computer music journal”, 7, 1983, pp. 43-55.
La musica elettronica. Testi scelti e commentati da Henri Pousseur; prefazione di Luciano Berio, Milano, Feltrinelli, 1976.
Mathews, Pierce 1991: Current directions in computer music research, edited by Max V. Mathews, John R. Pierce, Cambridge (Mass.), MIT Press, 1991.
McCaulay, Quatieri 1986: McCaulay, Robert J. - Quatieri, Thomas F., Speech analysis/synthesis based on a sinusoidalrepresentation, “IEEE transactions on acoustics, speech, and signal processing”, ASSP-34, 1986, pp. 744-754.
Palumbi, Seno 1999: Palumbi, Marco - Seno, Lorenzo, Physical modeling by directly solving wave PDE, in: Proceedings of International computer music conference, Beijing (China), october 22-27,1999, San Francisco, International Computer Music Association, 1999.
Puckette 2007: Puckette, Miller, The theory and technique of electronic music, Singapore, World Scientific, 2007 (anche in: http://www-crca.ucsd.edu/~msp/techniques.htm).
Roads 1996: Roads, Curtis, The computer music tutorial, Cambridge (Mass.), MIT Press, 1996.
Roads 2004: Roads, Curtis, Microsound, Cambridge (Mass.), MIT Press, 2004.
Von Helmholtz 1954: von Helmholtz, Hermann, On the sensation of tone, New York, Dover, 1954.
Tavola I
La percezione dei suoni
Le note musicali, rispetto agli altri suoni, sono intonate e cioè cantabili. Un suono del genere è un segnale periodico, o dotato di una prevalente componente periodica, il cui periodo si trova in banda audio. Questa è convenzionalmente definita tra i 20Hz e i 20KHz, ma in pratica è difficile incontrare intonazioni al di sopra dei 6KHz. La loro frequenza di ripetizione (intonazione) è misurata in intervalli definiti da specifici rapporti tra frequenze, dunque logaritmici. Le scale equabili delle musiche europee si basano sull’intervallo di ottava (un fattore due in frequenza), suddiviso in 12 intervalli detti semitoni e pari a un rapporto 12√2. L’intervallo doppio, pari a 6√2, è il tono. Le scale musicali alternano toni e semitoni entro l’ottava secondo schemi predefiniti (scala maggiore, minore, dorica, lidica ecc.), che sono a loro volta la base delle tonalità della musica classica o delle modalità della musica folklorica. La musica classica adotta scale di 7 note (da cui il termine ottava).
In italiano l’intonazione è indicata spesso come altezza, non senza una certa ambiguità dato che lo stesso termine è usato per indicare la prevalenza di componenti a frequenze acute anche in suoni non intonati (come quelli dei tamburi, che possono essere più o meno acuti a seconda delle loro dimensioni). Nella lingua inglese l’intonazione è invece indicata con il termine specifico pitch (intonazione), adottato anche in questo testo per le note in luogo di altezza.
Un segnale periodico ha uno spettro armonico, composto da righe di frequenze tutte multiple di una comune frequenza fondamentale corrispondente alla periodicità. Quando nello spettro del suono sono individuabili differenti pettini armonici sovrapposti, il nostro sistema uditivo è in generale in grado di separare le diverse periodicità e di individuare la presenza di più note. È questo il caso degli accordi musicali.
Un suono può avere una struttura spettrale non riconducibile a pettini armonici: in tal caso sarà un suono non intonato, aperiodico. Per indicare componenti spettrali generiche, senza implicazioni sui rapporti di frequenza, si utilizza il termine parziali in luogo di armoniche.
Se la struttura spettrale è continua, non mostra cioè picchi pronunciati, ma segue una curva dolce, e il segnale ha un carattere casuale, il corrispondente suono è percepito come una variante di fruscio (rumore bianco, rosa o diversamente colorato): qualcosa di simile al suono della pioggia battente, che può essere pensato come un treno di impulsi veloci e densi nel tempo, con temporizzazione casuale. Si tratta di quello che in teoria dei segnali viene chiamato rumore (rumore termico, rumore Schottky ecc.).
Lo spettro del moto vibratorio di piastre rigide e membrane elastiche vincolate sul bordo (per es., le pelli dei tamburi) è composto da picchi, espressione dei modi di vibrazione, tra i quali quelli a più bassa frequenza sono pronunciati e ben separati tra loro ma non armonici. Al crescere della frequenza le righe si addensano e si allargano rapidamente fino a costituire un continuo. Per questo motivo, strumenti basati su risonatori del genere emettono suoni non intonati, con componenti simili al rumore.
Oltre all’intonazione (o alla sua mancanza), all’intensità e alla collocazione nello spazio della sorgente, vi sono altri attributi riferibili ai suoni. Questi sono racchiusi nel timbro, che distingue per esempio due note identiche suonate da due strumenti differenti. Dobbiamo a Hermann L. F. von Helmholtz l’individuazione della correlazione tra profilo dei picchi spettrali e timbro. Si tratta comunque solo di una delle tante componenti di quest’ultimo, al quale contribuiscono anche altri fattori. La natura dei transitori complessivi e di quelli delle singole parziali, di relazioni non armoniche, la presenza di componenti di rumore e di modulazione delle parziali sono tutti attributi che contribuiscono a definire l’individualità dei suoni e quindi il loro timbro.
C’è infine un nesso tra note e parlato: le vocali sono infatti suoni intonati mentre le consonanti (specialmente quelle sorde) sono transitori o suoni a spettro continuo (alcune fricative, le sibilanti). La musica europea, e non solo europea, fino al Novecento è vocalica, con i suoni non intonati (tra i quali anche gli attacchi bruschi di suoni intonati, come negli strumenti a plettro o percussione) relegati al ruolo di elementi di transizione o puramente ritmici.
La questione della legittimità musicale della distinzione tra suoni e rumori agiterà l’estetica musicale per tutto il Novecento, durante il quale crescerà l’attenzione verso i suoni non intonati, il timbro e la collocazione spaziale. Aspetti prima marginali e poco esplorati occuperanno progressivamente un ruolo sempre più centrale nel pensiero musicale e compositivo sino a scalzare dal loro piedistallo intonazioni, scale, tonalità e modalità.
Tavola II
L’elettronica musicale analogica
La sintesi analogica è fondamentalmente sottrattiva: segnali generati da un oscillatore con una forma d’onda ricca di armoniche, oppure da modulazione o ancora segnali concreti, sono rimodellati spettralmente mediante filtri lineari. Questi assumono dunque un’importanza basilare e la disponibilità attorno agli anni Sessanta del controllo in tensione renderà possibile attribuire alla modellazione spettrale un carattere dinamico.
Tutti i circuiti diventeranno controllati in tensione: il VCA (Voltage controlled amplifier), il VCO (Voltage controlled oscillator), oltre al VCF (Voltage controlled filter). La possibilità di variare parametri significativi connettendo le uscite di un circuito all’ingresso di controllo di un altro permetteva di costruire complesse macchine musicali, al cuore delle quali vi era spesso un patch panel − una matrice di ingressi e uscite − che permetteva di interconnettere rapidamente i diversi dispositivi mediante cavi e connettori (patch).
Gli oscillatori analogici forniscono segnali periodici di varie forme d’onda (sinusoidi, onde quadre e triangolari, a dente di sega, a impulsi, trapezoidali) e quindi di diverso timbro di ampiezza e frequenza regolabili e controllabili anche in tensione.
Per la modellazione dello spettro si utilizzano tutti i classici filtri dell’elettronica: passa-basso (low-pass), passa-alto (high-pass), passa-banda (pass-band) e sopprimi-banda, elimina-frequenza (notch). Altri si rivelano particolarmente utili al trattamento del suono: i filtri risonanti e i filtri di presenza per esempio esaltano l’intorno di una determinata frequenza. I filtri a scaffale (low-shelf, high-shelf) presentano invece una sorta di pianerottolo rispettivamente alle basse frequenze o alle alte.
Altri filtri sono utili per manipolare la forma d’onda. Un filtro passa-tutto (all-pass) ha una caratteristica di ampiezza piatta, ma presenta un salto a forma di S orizzontale nella caratteristica di fase. Esso non altera il contenuto spettrale ma distorce la forma d’onda a causa della fase non lineare, allargando eventuali pacchetti di segnale concentrati nel tempo. Un comportamento questo qualitativamente simile a quello di un mezzo dispersivo. Alle basse frequenze, dove la caratteristica di fase è quasi lineare, il filtro presenta invece un ritardo di gruppo costante.
I filtri passa-tutto sono quindi adatti a simulare alle basse frequenze brevi tempi di volo, oppure il transito in mezzi dispersivi o diffusivi per segnali a banda larga.
Derivata dalle radiotrasmissioni, la modulazione di ampiezza consiste nel variare, mediante il segnale modulante, il guadagno di un VCA per il quale transita il segnale da modulare. Si ottiene in uscita il segnale originale più le frequenze somma e differenza delle parziali dei due segnali:
[A1∙cos(ωP∙t)+A2] B∙cos(ω2∙t)=A1∙B [cos((ωP+ω2) ∙t)
+cos((ωP−ω2) ∙t)] +A2∙B cos(ω2∙t).
Se si esegue invece il prodotto tra i due segnali utilizzando un moltiplicatore analogico si ha la cosiddetta modulazione di ampiezza a portante soppressa (in musica, modulazione a prodotto), nella quale il segnale modulato è assente in uscita:
A cos(ω1∙t)∙B cos(ω2∙t)=A B [cos((ω1+ω2)∙t)
+cos((ω1−ω2) ∙t))].
In entrambi i casi si ottengono due bande laterali, ciascuna popolata da un numero di parziali pari al prodotto dei numeri di parziali presenti nei due segnali originali, e conseguentemente una deformazione spettrale dei segnali modulati.
Il modulatore ad anello (ring modulator) rovescia invece il segno del segnale in ingresso in sincrono con una modulante di qualche centinaio di Hertz. L’operazione è equivalente al prodotto per un’onda quadra e il risultato è spettralmente molto ricco dato che questa è a banda larga.
I primi dispositivi erano costruiti mediante un ponte di diodi polarizzato dalla modulante e trasformatori telefonici per il disaccoppiamento tra ingresso e uscita.
Le rapide inversioni di segno producono un ronzio alla frequenza della modulante che nei primi modulatori ad anello era però poco percepibile perché filtrato dalla limitata banda dei trasformatori (tipicamente 8 KHz). Karlheinz Stockhausen ha utilizzato il ring modulator in diverse sue opere per elaborare suoni strumentali concreti.
Un inseguitore di inviluppo insegue le creste del segnale fornendo un’informazione sulla sua ampiezza locale. Si tratta di nient’altro che un rettificatore a doppia semionda, seguito da uno stadio di filtro passa-basso come negli stadi di alimentazione. Con esso è ad esempio possibile fornire a un circuito di sintesi un inviluppo ricavato da un segnale concreto.