Algebra

Algebra

L'algebra ha un rapporto singolare con il resto della matematica. Nella prefazione al suo libro del 1956, Fundamental concepts of algebra, Claude Chevalley affermava che l'algebra non è solo una parte della matematica; essa svolge nell'ambito della matematica quel ruolo che la matematica stessa ebbe per lungo tempo nella fisica. Ricordando, a questo proposito, un'osservazione di Eugene P. Wigner sulla "irragionevole efficacia" della matematica nelle scienze fisiche, ci si può chiedere se, similmente, l'algebra sia irragionevolmente valida per il resto della matematica. Lasciamo la risposta ai fatti. Viene spesso sottolineata la profondità di astrazione nella matematica di oggi. Mentre gli ottimisti la pongono entusiasticamente a un livello di attività intellettuale senza precedenti, i pessimisti non sono d'accordo e prevedono un periodo di stasi seguito da un periodo oscuro. In ogni modo, allo stato attuale delle cose, il dibattito stesso non sembra molto realistico, in quanto l'astrazione ha virtualmente sconfitto i suoi oppositori. In relazione ai diversi rami della matematica, è proprio nell'algebra che l'astrazione e il metodo assiomatico hanno raggiunto livelli senza precedenti e hanno avuto i maggiori successi. Questo è dovuto al fatto che, essendo le strutture algebriche molto vicine ai fondamenti, il metodo assiomatico fa miglior presa e può progredire più velocemente. Inoltre, queste strutture si presentano così spesso in altre parti della matematica, che l'averle assiomatizzate permette una notevole economia di pensiero.

Le due strutture algebriche predominanti, le sole che abbiano effettivamente importanza, sono i gruppi e gli anelli. Probabilmente la maggioranza degli algebristi, se non la loro totalità, concorda su questa affermazione, piuttosto dogmatica. Comunque, è opportuno precisare ulteriormente la situazione.

I sistemi dei numeri razionali e dei numeri reali erano noti già in tempi remoti (sebbene i numeri negativi e lo zero lo fossero solo implicitamente). Si può dire che i gruppi che si ottengono da questi sistemi di numeri, usando l'addizione e la moltiplicazione come operazioni, sono stati studiati dai matematici per oltre 2000 anni. Un primo esempio di gruppo in un contesto più sofisticato si trova nell'opera fondamentale che inaugurò la matematica del XIX sec.: le Disquisitiones Arithmeticae di Carl Friedrich Gauss (1801). Quando Gauss definì la composizione di forme quadratiche binarie, introdusse nella matematica un oggetto (che risultò poi essere un gruppo abeliano finito), nessuna proprietà cruciale del quale poteva considerarsi evidente a priori; in particolare, la legge associativa non era ovvia (a questo punto, potremmo accennare al fatto che, più tardi, Julius Wilhelm R. Dedekind presentò il gruppo in questione in modo più convenzionale, essenzialmente come un gruppo moltiplicativo di ideali in un certo anello).

La teoria dei gruppi ebbe un ruolo chiave nelle importanti scoperte di Évariste Galois, nelle quali tuttavia intervenivano soltanto i gruppi di permutazioni; l'idea astratta di gruppo apparteneva ancora al futuro, ma erano già poste le nozioni fondamentali di sottogruppo normale, di serie di composizione, di risolubilità. In un lavoro pubblicato nel 1854, Arthur Cayley giunse molto vicino a porre la definizione moderna di gruppo astratto. Gradualmente, questo concetto mise le sue radici e l'importante libro di William Burnside (Theory of groups of finite order), apparso proprio all'inizio del nuovo secolo, pose le basi per il suo sviluppo successivo.

I gruppi e gli anelli possono essere dotati di strutture addizionali (strutture topologiche, ordinamenti, strutture algebrico-geometriche, insiemi duali di operazioni, ecc.). Un posto d'onore spetta ai moduli che, in certo qual modo, coinvolgono sia la struttura di gruppo sia quella di anello. Inoltre, esistono metodi significativi di indebolire gli assiomi (per es., studiare semigruppi invece di gruppi, o, nel caso degli anelli, sostituire la legge associativa con altre leggi).

Vi sono infine teorie con un altissimo grado di generalità come la teoria delle categorie e l'algebra universale, che in un certo senso pervadono tutta l'algebra, gruppi e anelli inclusi. Fatte queste precisazioni, cominciamo con una parte generale sui gruppi; tratteremo poi alcuni aspetti particolari della teoria. Affronteremo poi la teoria degli anelli, gli anelli di gruppo e la relativa teoria delle rappresentazioni dei gruppi, e concluderemo con la teoria degli anelli commutativi e i suoi legami con la geometria algebrica.

Gruppi in generale

Oggi gli assiomi di gruppo sono posti di solito comesegue: è dato un insieme G, sulla cui natura non si dice nulla, salvo che su G è definita un'operazione binaria con certe proprietà. Tale operazione è una funzioneche assegna a ogni coppia di elementi a e b di G unterzo elemento di G, che si indica spesso semplicemente con ab.

Si impongono all'operazione binaria tre assiomi: (a) legge associativa (ab)c=a(bc); (b) esistenza di un elemento neutro e, o unità, tale che ea=ae=a per ogni a (l'unicità di e segue immediatamente dalla legge associativa); (c) esistenza per ogni a di un inverso a⁻¹, tale che aa⁻¹=a⁻¹a=e (la legge associativa assicura anche l'unicità di a⁻¹). Si può anzi esigere un po' meno, in quanto bastano una unità a destra (ae=a) e un inverso a destra (aa⁻¹=e), oppure un'unità e un inverso a sinistra. Ma si presenta a questo punto una complicazione curiosa: assumendo, per esempio, unità a destra e inversi a sinistra, si ottiene qualcosa di più generale di un gruppo, la cui struttura è stata più volte discussa nella letteratura. È possibile dare assiomi per i gruppi senza fare intervenire gli assiomi di esistenza, usando un'unica operazione binaria e delle identità soddisfatte da essa; comunque, gli assiomi che ne risultano non sono molto eleganti.

Le nozioni chiave nella teoria dei gruppi sono quelle di omomorfismo, nucleo, sottogruppo normale e gruppo quoziente. Il concetto di omomorfismo può essere formulato per strutture molto generali. Un omomorfismo è un'applicazione da una struttura in un'altra, che conserva le proprietà rilevanti per le due strutture. Per i gruppi, un omomorfismo è un'applicazione f da un gruppo G a un altro, che soddisfa la condizione: f(ab)=f(a)f(b) per tutti gli a e b in G. Non è necessario richiedere che f conservi l'elemento unità e gli inversi, perché ciò è una conseguenza. Il sottoinsieme di G, costituito da tutti gli elementi la cui immagine mediante f è l'elemento neutro dell'altro gruppo, è un sottogruppo K di G, cioè un sottoinsieme di G che è esso stesso un gruppo rispetto alla stessa operazione di G. Il sottogruppo K si chiama nucleo di f. Il nucleo non è un sottogruppo qualunque di G; esso ha una proprietà in più: per ogni a in K e x in G, x⁻¹ax appartiene a K. Un sottogruppo con questa proprietà si dice normale. Si può formare il gruppo quoziente, che si denota con G/K, di G rispetto a un sottogruppo normale K, eliminando, in un certo senso, gli elementi di K.

Un omomorfismo biunivoco è un isomorfismo; un isomorfismo di un gruppo su se stesso è un automorfismo. La presenza di un sottogruppo normale K in un gruppo G ci permette una decomposizione di G nei due gruppi K e G/K. In tal modo possiamo ridurre, in molti casi, dei problemi su G a problemi analoghi su K e su G/K, e questo ci induce a considerare quei gruppi che non hanno sottogruppi normali (eccetto, ovviamente, i due sottogruppi banali costituiti, rispettivamente, da tutto G e dall'insieme che ha come unico elemento e). Il seguente teorema è dovuto a Joseph-Louis Lagrange: se G è un gruppo finito e H è un suo sottogruppo, l'ordine di H (l'ordine di un gruppo finito è il numero degli elementi che esso contiene) divide l'ordine di G. Pertanto, un gruppo il cui ordine sia un numero primo non ha sottogruppi non banali, né normali né non normali; un tale gruppo non è interessante. Perciò diciamo che un gruppo è semplice se, oltre a non avere sottogruppi normali non banali, non è finito di ordine primo. L'uso del termine semplice è in questo caso paradossale, perché lo studio dei gruppi semplici è di fatto molto complicato.

Gruppi semplici finiti

Nel discutere la struttura dei gruppi semplici finiti cercheremo di seguire lo sviluppo di tale argomento fino ai nostri giorni. Cominciamo con gli esempi classici, esaminando anzitutto il gruppo S_n delle permutazioni di n elementi, il cosiddetto gruppo simmetrico di grado n. Per n≤4, questi gruppi sono all'estremo opposto della semplicità: sono risolubili. Un gruppo G si dice commutativo o abeliano se ab=ba per tutti gli a e b in G (il nome abeliano è in onore del matematico norvegese Niels Abel per il suo lavoro del 1829 che tratta, per dirla con linguaggio moderno, di equazioni algebriche aventi un gruppo di Galois abeliano). G si dice risolubile se può essere ottenuto da un numero finito di gruppi abeliani, cioè se esiste una catena di sottogruppi

[1] G = G₀ ⊃ G₁ ⊃ G₂ ⊃ … ⊃ G_n = e

tale che ogni G_i+1 sia normale in G_i e ogni G_i /G_i+1 sia di ordine primo. L'aggettivo risolubile deriva dal legame, posto in luce dalla teoria di Galois, con la risolubilità per radicali di un'equazione algebrica, e il fatto che le equazioni polinomiali in una variabile siano risolubili per radicali fino al quarto grado trova la sua spiegazione nella risolubilità di S_n per n≤4.

tab. 1

Per n≥5, S_n non è più risolubile e non è neppure semplice, anche se gli manca poco per esserlo. Infatti, S_n ha un solo sottogruppo normale proprio: esso consiste di tutte le permutazioni pari, viene chiamato gruppo alterno di grado n e si denota con A_n (una permutazione è pari se si ottiene con un numero pari di scambi successivi di due elementi; si può dimostrare che se tali scambi sono in numero pari, ciò è indipendente dal modo in cui essi vengono effettuati). Il gruppo A_n è semplice e il suo ordine è n/2. I gruppi alterni A_n, per n≥5, formano la nostra prima famiglia infinita di gruppi semplici finiti non abeliani. Per avere altri esempi di gruppi semplici, consideriamo i gruppi di matrici e partiamo dal gruppo lineare GL_n(F) di tutte le matrici n×n non singolari su un corpo F. Il gruppo GL_n(F) non è semplice, ma possiamo ottenere da esso uno semplice effettuando delle opportune riduzioni. Con una prima riduzione si sostiuisce a GL_n(F) il gruppo unimodulare (o lineare speciale) SL_n(F), consistente delle matrici con n×n determinante 1; una seconda riduzione si ottiene considerando il gruppo quoziente di SL_n(F) rispetto al suo centro (il centro di un gruppo consiste degli elementi che commutano con ogni elemento del gruppo; nel nostro caso è il sottogruppo delle matrici scalari). Otteniamo così il gruppo unimodulare proiettivo, che una volta si indicava con PSL_n(F) e oggi più semplicemente con L_n(F). Questo gruppo è semplice per tutti gli F e gli n, eccetto in due casi: quando n=2 ed F è il corpo di 2 o 3 elementi. Così quando F è finito, otteniamo la nostra seconda famiglia infinita di gruppi semplici finiti classici. Queste due famiglie esauriscono i primi gruppi semplici finiti, come è illustrato nella tab. 1 (nella nostra notazione, F_q è l'unico corpo finito con q elementi; q deve essere una potenza di un numero primo).

tab. 2

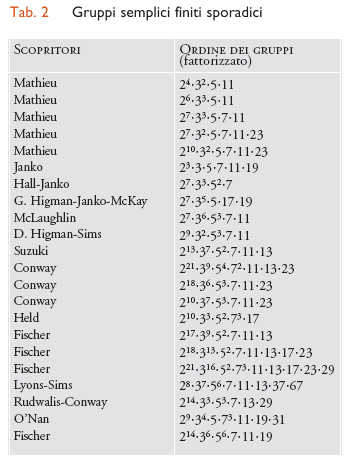
A questo punto, senza entrare nei dettagli, enunciamo brevemente gli aspetti rimanenti. Nello studio dei gruppi di Lie (gruppi topologici, nei quali un intorno dell'identità può essere parametrizzato da uno spazio euclideo, in modo che le operazioni di composizione del gruppo siano analitiche) esiste una classificazione dei gruppi 'semplici' (mettiamo semplice tra virgolette perché, nel contesto dei gruppi di Lie, ha un significato un po' differente). Tale classificazione risale a Wilhelm Killing e Henri Cartan. Vi sono dei gruppi puramente algebrici, analoghi ai gruppi suddetti, che si possono costruire su un corpo arbitrario F; L_n(F) ne è un esempio. Ma le cose si complicano quando F non è algebricamente chiuso. Questo caso richiede opportune varianti dei gruppi di Lie semplici; il più facile a descriversi è il gruppo unitario, che si ottiene dal gruppo lineare. Richiese parecchio tempo agli algebristi selezionare i fatti rilevanti e portare a compimento la costruzione; a tal fine ebbe un ruolo importante un lavoro di Chevalley del 1955, esposto diffusamente da Cartan nel 1965. Oggi, il concetto di gruppo semplice finito di tipo Lie è pienamente chiarito. Vi sono altri gruppi semplici finiti, oltre quelli alterni e di tipo Lie? La risposta è affermativa. Nel 1861, Emile Mathieu trovò altri cinque gruppi, indicati di solito con M₁₁, M₁₂, M₂₂, M₂₃, M₂₄ (ove l'indice si riferisce al numero degli elementi che appaiono in una loro rappresentazione naturale come gruppi di permutazione). Poi, per oltre 100 anni, non si trovarono altri gruppi semplici; sicché fu una vera sorpresa quando, nel 1965, Zvonimir Janko ne scoprì uno di ordine 175.560. Da allora ne sono venuti fuori numerosi altri, indicati collettivamente con l'appellativo di sporadici, termine già usato da Burnside per i gruppi di Mathieu (tab. 2).

Gruppi infiniti

La teoria dei gruppi infiniti ha un sapore ben diverso da quella dei gruppi finiti. È vero che le nozioni di semplicità e di risolubilità conservano il loro significato, sebbene, per quanto riguarda la seconda, vi siano varie nozioni di risolubilità transfinita che si possono condividere. È anche vero che i gruppi alterni e quelli del tipo di Lie trovano degli analoghi tra i gruppi infiniti, ma gli algebristi sono ben lontani dall'averne un quadro adeguato. I gruppi infiniti sono troppi e, forse, essi non saranno mai completamente classificati. La questione è del tutto differente se ci limitiamo a gruppi con qualche struttura addizionale significativa. Tra i gruppi così arricchiti, i più importanti sono i gruppi algebrici e quelli topologici; ma essi vanno oltre lo scopo del presente lavoro. Importante è il problema se un gruppo, soggetto a una o più delle condizioni soddisfatte da tutti i gruppi finiti, sia necessariamente finito. A questo proposito il problema di Burnside, posto nel 1902, è il più famoso. Esso si presenta in due forme: (a) il problema generale di Burnside. Se G ha un numero finito di generatori (un sottoinsieme S di G è un insieme di generatori per G se tutti gli elementi di G possono essere ottenuti dagli elementi di S tramite combinazioni di operazioni definite su G) e tutti i suoi elementi sono di ordine finito, G è finito? (b) Il problema ristretto di Burnside. Se G ha un numero finito di generatori ed esiste un r tale che x^r=1 per tutti gli x in G, G è finito?

Il problema generale di Burnside fu risolto da Evgenij S. Golod nel 1964, come sottoprodotto del notevole lavoro che egli fece in collaborazione con Igor R. Shafarevich e che condusse a un esempio di torre infinita di corpi di classi nella teoria dei numeri algebrici. Allo stesso tempo, Golod diede un controesempio all'analogo del problema di Burnside nella teoria degli anelli. Dopo alcune comunicazioni preventive, modificate successivamente, nel 1968 Sergei Adjan e Pëtr S. Novikov pubblicarono una dimostrazione del fatto che il problema ristretto di Burnside ha una risposta negativa quando r è dispari e maggiore o uguale a 4381. Si tratta di un lavoro complicato, con più di cento lemmi. Nel 1975, Adjan ha migliorato questo risultato dimostrando che la risposta è negativa per r dispari e maggiore di 665. Nel 1992, Sergei V. Ivanov ha provato che la risposta è negativa per r≥13. La risposta al problema ristretto di Burnside è affermativa per r=2 (banale), r=3 (Burnside 1912), r=4 (Ivan N. Sanov 1940) e r=6 (Marshall Hall 1957). È possibile che in tutti gli altri casi la risposta sia negativa. C'è un'osservazione da fare. Nel caso r=3, Burnside non diede correttamente l'ordine del gruppo; l'errore fu corretto da Friedrich Levi e Bartel L. van der Waerden nel 1932. [Efim Zelmanov ha ricevuto la medaglia Fields nel 1994 per la risoluzione del problema ristretto di Burnside, dimostrando che esiste un numero finito di gruppi con un numero finito di generatori e r limitato. n.d.r.].

Vi è un tipo di gruppo infinito che è, in un certo senso, all'estremo opposto dei gruppi finiti. Tale tipo è quello dei gruppi liberi. Daremo una descrizione semplificata del gruppo libero a due generatori, x e y. In primo luogo, essendo generato da x e y, ogni suo elemento può scriversi nella forma …x ⁱy ^jx ^ky ^m…, dove i, j, k, m… sono interi (positivi, negativi o nulli). La condizione che ne fa un gruppo libero è che queste espressioni siano uniche. Non possiamo richiedere incondizionatamente tale proprietà, perché, per esempio, il termine x⁰ può essere soppresso e allora le due potenze di y vicine a x⁰ a sinistra e a destra possono essere unite; nel caso siano della forma yⁱ e y⁻ⁱ, possono essere soppresse anch'esse, e così via. Si chiede allora l'unicità a meno di queste semplificazioni. Dare una buona definizione di gruppo libero e provarne l'esistenza comporta alcune difficoltà tecniche, non insormontabili.

Una costruzione di questo tipo è usata spesso nella matematica moderna, soprattutto in algebra. A seconda del contesto, la si può descrivere come la costruzione di un oggetto libero soggetto a certe condizioni o come la soluzione di un conveniente problema universale. Vi sono per i gruppi liberi alcuni problemi che sembrano molto semplici ma che risultano sorprendentemente difficili: per esempio il fatto che a²=b² implica a=b è vero ma è tutt'altro che facile da dimostrare. I gruppi liberi sono utili nello studio dei gruppi in generale. Per esempio, sia G un gruppo generato dagli elementi g_i (in numero finito o infinito). Costruiamo il gruppo libero F con generatori x_i, con un x_i per ogni g_i. Allora (e questa è una proprietà cruciale dei gruppi liberi) esiste un unico omomorfismo di F su tutto G, che manda x_i su g_i per ogni i. Pensando al nucleo K di questo omomorfismo come a qualche cosa che descrive le relazioni tra i generatori g_i di G, si parla di una presentazione di G per mezzo di generatori e relazioni. Tale modo di presentare un gruppo ha un'applicazione suggestiva nella teoria dei nodi (probabilmente al lettore basta l'idea intuitiva di nodo; per un topologo, un nodo è un omomorfismo di un cerchio nello spazio euclideo a tre dimensioni). È facile leggere, da un conveniente diagramma rappresentante un nodo, quali sono i generatori e le relazioni per il gruppo fondamentale del complementare del nodo.

Quest'ultimo gruppo è l'invariante più importante legato a un nodo e gli studiosi di teoria dei nodi hanno trovato metodi potenti per analizzare generatori e relazioni di gruppi, con un particolare interesse per i gruppi speciali che si trovano nella teoria dei nodi. Molta attenzione richiede dimostrare che ogni sottogruppo di un gruppo libero è libero. Sotto ipotesi di finitezza si può migliorare l'enunciato dicendo che, se G è libero con n generatori e H è un sottogruppo di G di indice k (ciò significa che G è esattamente l'unione di k sottoinsiemi della forma Ha, chiamati classi laterali destre di H in G), allora H è libero con k(n−1)+1 generatori. La questione ha legami complessi con la topologia. In topologia, a ogni spazio topologico è assegnato un gruppo, detto gruppo fondamentale (già incontrato in relazione ai nodi). Per grafo intendiamo una collezione di punti, alcuni dei quali sono uniti da segmenti; a ogni grafo è associato uno spazio topologico molto semplice, che i topologi chiamano complesso di dimensione uno. Esiste un teorema secondo cui il gruppo fondamentale di un grafo è un gruppo libero; in base a esso si ottiene una bella dimostrazione del teorema sui sottogruppi dei gruppi liberi (incluse le questioni riguardanti il numero dei generatori).

Anelli e corpi

Un anello è un insieme dotato di due operazioni, dette addizione e moltiplicazione e indicate nel modo usuale. Per l'addizione, l'anello deve essere un gruppo abeliano; inoltre, si richiede che l'addizione sia legata alla moltiplicazione dalle due leggi distributive:

[2] a(b + c) = ab + ac (b + c)a = ba + ca.

Per la moltiplicazione, gli algebristi non sono d'accordo se sia meglio richiedere o meno un elemento neutro, detto unità (e cioè un elemento, che viene anche indicato col simbolo 1, tale che 1a=a1=a per ogni a). Per i nostri propositi, considereremo qui soltanto gli anelli dotati di un elemento unità. Non abbiamo ancora detto nulla sulla legge associativa della moltiplicazione, (ab)c=a(bc), ma di solito il termine anello è usato tacitamente per anello associativo. Se si esclude l'associatività, si parla di anello non associativo per quanto sarebbe più appropriato dire anello non necessariamente associativo.

Dal confronto fra la struttura di gruppo e quella di anello si è portati a cercare, per la struttura di anello, concetti analoghi a quelli di sottogruppo e sottogruppo normale. Il primo ci è fornito dalla nozione di sottoanello, che è un sottoinsieme chiuso rispetto alle operazioni dell'anello (e di solito si richiede che contenga anche l'elemento unità dell'anello). Per il secondo, si hanno tre nozioni: ideale sinistro, ideale destro e ideale bilatero. Un ideale sinistro I, in un anello R, è un sottoinsieme di R che è un sottogruppo additivo e che soddisfa la condizione RI⊂I, cioè I assorbe la moltiplicazione a sinistra per elementi arbitrari di R. La definizione di ideale destro è analoga; un ideale è bilatero se è contemporaneamente un ideale sinistro e destro. Quella di ideale bilatero è la nozione analoga a quella di sottogruppo normale. Il nucleo di un omomorfismo è un ideale bilatero e se I è bilatero si può formare l'anello quoziente R/I.

Un altro importante concetto è quello di modulo su un anello associativo R. Un modulo A su R è un gruppo abeliano additivo, che ammette una moltiplicazione (a sinistra, per fissare le idee) fra gli elementi di A e gli elementi di R tale che i prodotti così ottenuti siano ancora in A. In modo forse un po' impreciso ma espressivo, si può dire che gli assiomi sono tutti quelli che postulano tutte le possibili leggi associative. La nozione di sottomodulo B di A è quella ovvia, e possiamo costruire in modo naturale un modulo quoziente A/B. I moduli contribuiscono a illustrare il ruolo degli ideali unilateri nella teoria degli anelli. Infatti, un ideale sinistro in un anello R non è che un sottomodulo di R, quando si considera R come modulo sinistro su se stesso. Un corpo è un anello nel quale gli elementi non nulli costituiscono un gruppo rispetto alla moltiplicazione; se tale gruppo moltiplicativo è anche commutativo allora si parla di corpo commutativo o campo. Nel seguito useremo sempre il termine corpo, senza specificare se il corpo considerato sia commutativo o meno, poiché ciò apparirà chiaro di volta in volta dal contesto. Esempi fondamentali sono i corpi dei numeri razionali, dei numeri reali, dei numeri complessi e degli interi modulo p per ogni numero primo p. Lo studio dei corpi comincia con l'osservazione che ogni corpo K contiene un unico sottocorpo minimo, detto sottocorpo primo, che è il corpo dei numeri razionali oppure quello degli interi modulo p, per un certo p. Si dice allora che la caratteristica di K è 0 o p, rispettivamente.

A partire da un corpo dato, si possono ottenere altri corpi costruendo degli ampliamenti. Quando si amplia un corpo K a un nuovo corpo K(u) aggiungendo un elemento u si presentano due casi: u non soddisfa alcuna equazione algebrica a coefficienti in K e allora u si dice trascendente su K, altrimenti si dice che u è algebrico su K. Partendo dal sottocorpo primo di un corpo K si può ottenere tutto K con una successione (in generale transfinita) di aggiunzioni di elementi. Si dice che K è algebricamente chiuso se non ammette ampliamenti algebrici. Dal teorema fondamentale dell'algebra (dimostrato per la prima volta da Gauss) sappiamo che il corpo dei numeri complessi è algebricamente chiuso. La teoria dei corpi è utile per sistemare e semplificare questioni concernenti gli ampliamenti algebrici. Un esempio significativo è lo studio delle costruzioni con riga e compasso nella geometria euclidea. Qui è necessario disporre del concetto di grado [L:K] di un corpo L, ampliamento di K: esso è la dimensione di L come spazio vettoriale su K. Il risultato è che, partendo da punti con coordinate razionali, possiamo raggiungere un certo punto mediante una costruzione con riga e compasso se e solo se, le sue coordinate appartengono a un corpo N ottenuto per ampliamenti quadratici successivi a partire dal corpo dei razionali ℚ. Pertanto [N:ℚ] è una potenza di 2. Supponiamo ora di voler dividere l'angolo di 60° in tre parti uguali; dovremmo poter mettere cos 20° in una tale successione di ampliamenti, il che è impossibile in quanto il grado [ℚ(cos 20°):ℚ] è 3.

La teoria degli ampliamenti di dimensione finita di corpi è dominata dalla teoria di Galois. In linguaggio moderno, l'idea di Galois fu di studiare una coppia di corpi K⊂L introducendo il gruppo G di quegli automorfismi di L che lasciano fisso ogni elemento di K. È possibile che G lasci fissi altri elementi oltre quelli di K; se il sottocorpo fisso è esattamente K, allora si dice che L è normale su K. Il teorema più importante della teoria di Galois asserisce che esiste una corrispondenza biunivoca tra i sottogruppi di G e i corpi che stanno tra K e L, e che, inoltre, tale corrispondenza ha altre proprietà interessanti. Questo teorema ci dà la possibilità di ridurre molte questioni della teoria dei corpi a questioni della teoria dei gruppi, dove si hanno già alcune informazioni. Per esempio, possiamo vedere subito che vi è solo un numero finito di corpi intermedi tra un corpo e un suo ampliamento normale; questo fatto, tradotto nel linguaggio della teoria dei gruppi, dice semplicemente che un gruppo finito ha un numero finito di sottogruppi.

L'applicazione più spettacolare della teoria di Galois (applicazione che ispirò lo stesso Galois) è la dimostrazione che le equazioni algebriche di grado maggiore o uguale a 5 non sono in generale risolubili per radicali, cioè mediante estrazioni di radici combinate con operazioni razionali. Si dimostra, più in generale, che se L è normale su K, allora L è ottenibile da K aggiungendo radicali se e solo se, il gruppo di Galois di L su K è risolubile. Così, il problema di risolvere le equazioni algebriche per radicali si riduce al fatto che il gruppo simmetrico S_n è risolubile se e solo se n≤4. La teoria di Galois presenta varie questioni non ancora risolte, tra le quali emerge la seguente: dato un gruppo finito G, esiste un ampliamento normale del corpo dei numeri razionali con gruppo di Galois isomorfo a G? Per scelte particolari di G, la risposta è nota ed è affermativa; esempi sono dati dal gruppo simmetrico S_n, dal gruppo alterno A_n e da tutti i gruppi risolubili. Inoltre, se si è liberi di scegliere il corpo iniziale, non è difficile trovare una coppia di corpi il cui gruppo di Galois sia un qualsiasi gruppo finito preassegnato.

A tale scopo, si parte da un corpo k e gli si aggiungono n indeterminate, ottenendo così il corpo L=k(x₁,x₂,…,x_n). Il gruppo simmetrico S_n agisce su L permutando tra loro le x_i e il corpo K, che esso lascia fisso, è il corpo di tutte le funzioni razionali simmetriche nelle x_i con coefficienti in k. Il corpo L è normale su K con gruppo di Galois S_n. Sappiamo, dalla teoria di Galois, che ogni sottogruppo di S_n è il gruppo di Galois di L su un conveniente corpo intermedio; poiché ogni gruppo finito può essere considerato come un sottogruppo di qualche S_n, si può vedere così ogni gruppo finito come un gruppo di Galois.

Anelli di gruppo e rappresentazioni dei gruppi

L'anello di gruppo RG di un gruppo G su un anello commutativo R consta di tutte le espressioni ∑a_ig_i con a_i in R e g_i in G. Gli anelli di gruppo sono ricche sorgenti di esempi: da ogni gruppo G e da ogni anello di coefficienti R si ottiene un nuovo anello RG. Ma la loro importanza sta nel fatto che essi costituiscono un legame tra la teoria dei gruppi e quella degli anelli, il che apre una nuova prospettiva nello studio dei gruppi. Ciò accade, soprattutto, perché vi è un legame tra moduli su gruppi e moduli su anelli. Infatti, con l'ovvia definizione di G-modulo (o rappresentazione di G) come R-modulo su cui opera G, vi è una corrispondenza biunivoca tra G-moduli e RG-moduli. È naturale chiedersi in quali casi la teoria dei moduli su un dato anello si comporti particolarmente bene. La cosa più desiderabile è che ogni modulo sia somma diretta di moduli irriducibili, cioè privi di sottomoduli propri. A questo punto enunciamo un teorema, che abbiamo omesso dal nostro panorama sugli anelli, posponendolo fino a ora: un anello ha la proprietà che tutti i suoi moduli sono somme dirette di moduli irriducibili se e solo se, è semisemplice artiniano; un anello artiniano è un anello in cui ogni successione decrescente di i duali è stazionaria (condizione della catena decrescente).

Se R è un corpo (chiamiamolo F) e G è un gruppo finito, allora FG è un'algebra di dimensione finita su F. Quando essa è semisemplice? La risposta è data da un teorema di Heinrich Maschke (1899), aggiornato in modo da valere per tutti i corpi possibili. Se F ha caratteristica p≠0, F è semisemplice se e solo se, l'ordine di G è primo con p. Il caso in cui l'ordine di G è divisibile per p è stato studiato a fondo da Richard Brauer e dalla sua scuola. La teoria dei caratteri modulari che ne risulta fornisce i fondamenti per la costruzione dei caratteri ordinari, che sono quelli ottenuti sul corpo dei numeri complessi. Nel caso semisemplice, per i nostri propositi possiamo prendere come corpo F quello dei numeri complessi. La teoria dei moduli su un anello artiniano semisemplice A rivela che gli A-moduli irriducibili sono in corrispondenza biunivoca con le parti semplici che costituiscono A. Ritornando a FG, osserviamo che ogni sua parte semplice è l'algebra di tutte le matrici r_i×r_i su F, per un certo intero r_i che è detto grado della corrispondente rappresentazione irriducibile di G. Osserviamo inoltre che una delle r_i è uguale a 1, perché abbiamo la rappresentazione banale di G, che applica ogni elemento nella matrice identità 1×1. Vale inoltre l'equazione ∑r²_i=n, dove n è l'ordine di G. Già più notevole è il fatto secondo cui ogni r_i divide n. Il caso in cui G è abeliano non presenta alcun interesse, in quanto tutte le r_i (e sono n) sono uguali a 1. Il primo esempio non commutativo è offerto dal gruppo di ordine 6, S₃, o gruppo simmetrico su tre oggetti. Vi sono due rappresentazioni di dimensione 1, in realtà rappresentazioni del gruppo quoziente S₃/A₃, e due rappresentazioni irriducibili di dimensione 2. L'identità 6=1²+1²+2² offre una verifica delle affermazioni precedenti.

Più della rappresentazione stessa, è invariante la funzione che si ottiene assegnando a ogni elemento del gruppo la traccia della matrice che lo rappresenta (la traccia di una matrice è la somma di tutti gli elementi della diagonale principale). Tale funzione è detta carattere e, se la rappresentazione è irriducibile, carattere irriducibile. Notiamo che, a differenza della rappresentazione stessa, il carattere della rappresentazione è indipendente dalla scelta della base nello spazio vettoriale su cui la rappresentazione opera. Inoltre, un carattere è in realtà una funzione sulle classi coniugate del gruppo (due elementi a, b in un gruppo sono coniugati se esiste un elemento x per cui x⁻¹ax=b; una classe di coniugio consiste di tutti gli elementi coniugati a un elemento dato) e il numero dei caratteri irriducibili (e quindi il numero delle rappresentazioni irriducibili) è uguale al numero delle classi di coniugio. I caratteri soddisfano certe relazioni di ortogonalità. Tutte queste informazioni sommate insieme sono di grande aiuto nella costruzione della tavola dei caratteri del gruppo. È accaduto più di una volta che nella ricerca di un gruppo sporadico semplice fosse già disponibile, almeno in parte, la tavola dei caratteri, prima ancora di sapere se questo gruppo fantasma esistesse effettivamente.

Anelli commutativi

La teoria degli anelli commutativi ha due fonti principali: (a) la teoria dei numeri algebrici che, iniziata con Gauss, fu plasmata a opera di Eduard E. Kummer, Dedekind, Peter Gustav Dirichlet e Leopold Kronecker, e raggiunse livelli elevatissimi con David Hilbert; (b) la geometria algebrica, sviluppata da molti matematici tedeschi e italiani. Tuttavia, mentre la teoria dei numeri algebrici riguarda il caso di dimensione 1 e gli anelli artiniani quello di dimensione 0, la geometria algebrica rappresenta il caso generale. Poiché i numeri algebrici e la geometria algebrica non rientrano nel quadro generale delineato in questo articolo, ci occuperemo della teoria degli anelli commutativi come di una disciplina autosufficiente e ci volgeremo solo occasionalmente alle origini storiche. La teoria degli anelli commutativi è dominata dal concetto di ideale primo; un ideale I in un anello commutativo R è primo se ogniqualvolta un prodotto ab è in I o a o b appartiene a I. In altri termini, possiamo dire che I è primo se R/I è un campo d'integrità (non ha divisori dello zero). In un anello non commutativo, il modo proprio di generalizzare la nozione di ideale primo è di supporre che aRb⊂I implichi che a o b è in I. Naturalmente, potevamo anche copiare semplicemente la definizione del caso commutativo e dire che I è primo se ab∈I implica che a o b è in I, ma tale proprietà è troppo raramente soddisfatta per essere utile.

Per quanto vi siano anche numerosi risultati sugli ideali primi di anelli non commutativi, qui ci occuperemo soltanto del caso commutativo. D'ora in poi quindi per anello intenderemo anello commutativo. Indichiamo sommariamente in quale modo gli anelli commutativi nascano dalla geometria algebrica e come in essa si inquadrino gli ideali primi. In geometria algebrica si lavora con equazioni algebriche nelle variabili x₁,x₂,…,x_n su un dato corpo k algebricamente chiuso (nel caso classico, il corpo dei numeri complessi). Una varietà V è l'insieme di tutti i punti che soddisfano una famiglia di equazioni algebriche. Una varietà è, in modo essenzialmente unico, unione di un numero finito di varietà che sono irriducibili, nel senso che non possono essere decomposte in altre varietà. Sia V una varietà irriducibile e P l'insieme di tutti i polinomi che si annullano su V, allora P è un ideale primo nell'anello k[x₁,…,x_n] dei polinomi in x₁,…,x_n con coefficienti in k; in tal modo si ottiene una corrispondenza biunivoca tra le varietà irriducibili e gli ideali primi e a V corrisponde il campo di integrità k[x₁,…,x_n]/P. Riassumendo, le varietà sono legate agli ideali primi e anche ai campi d'integrità con un numero finito di generatori su un corpo.

Si è usato il termine varietà, ma sarebbe stato più esatto parlare di varietà affine. La geometria algebrica si occupa delle varietà proiettive, ma esistono varietà ancora più generali che comprendono le varietà affini, quelle proiettive e altre ancora. In due lavori del 1893 e del 1895 diventati classici Hilbert dimostrò due dei teoremi fondamentali su questo argomento. Il primo asserisce che ogni ideale in k[x₁,…,x_n] ha un numero finito di generatori se k è un corpo. L'importanza di quest'ultima condizione fu messa in rilievo da Emmy Noether in un articolo del 1921 e, in seguito a ciò, si chiamarono noetheriani quegli anelli in cui ogni ideale ha un numero finito di generatori o, equivalentemente, in cui gli ideali soddisfano la condizione della catena ascendente (notiamo che in un certo senso gli anelli artiniani, dove vale la condizione della catena discendente, sono i duali di quelli noetheriani; ma si tratta di una dualità un po' strana). Nel 1939, Frederik G. Hopkins dimostrò che la condizione della catena discendente implica quella della catena ascendente anche in anelli non commutativi.

Oggi, il teorema di Hilbert si enuncia e si dimostra nella forma seguente: se R è noetheriano anche R[x] è noetheriano. Vale la pena di osservare che, in questa forma, la dimostrazione è più agevole; è vero che si ha a che fare con un anello dei coefficienti molto generale, ma è un prezzo che si può pagare per ottenere il vantaggio di lavorare in una sola variabile. Il secondo teorema fondamentale di Hilbert è il Nullstellensatz, che si può enunciare in numerose forme differenti. Ne abbiamo già dato una versione, senza specificare che fosse il Nullstellensatz, quando abbiamo parlato della corrispondenza biunivoca tra varietà irriducibili e ideali primi. Ne daremo un'altra formulazione connessa con il metodo che si usa in analisi funzionale per trattare gli anelli di funzioni. Nell'anello k[x₁,…,x_n] dei polinomi in n variabili su un corpo k algebricamente chiuso, consideriamo l'insieme dei polinomi che si annullano in un punto; esso è un ideale massimale. Il Nullstellensatz asserisce che tutti gli ideali massimali si ottengono in questo modo. La teoria degli anelli commutativi, nello stile del XX sec., ebbe inizio nel 1905 da un articolo di Emanuel Lasker. Egli dimostrò che in k[x₁,…,x_n] ogni ideale è un'intersezione di ideali primari (omettiamo la definizione esatta di ideale primario; è sufficiente notare l'analogia del teorema di Lasker con l'espressione di un intero come prodotto di potenze di interi primi). Sedici anni dopo, Emmy Noether dimostrò con un ragionamento breve e molto elegante la proprietà suddetta quando è soddisfatta la condizione della catena ascendente. Nacque così la teoria degli anelli noetheriani.

Sia ora P un ideale primo in un anello R. Consideriamo tutte le catene di ideali primi discendenti da P. La massima lunghezza di una tale catena ha due nomi nella letteratura: rango e altezza; noi useremo il primo. Il rango può essere infinito, ma un teorema di Wolfgang Krull (1928) dice che nel caso noetheriano il rango è finito. Anzi, è possibile una valutazione accurata: se P è minimale in un ideale generato da n elementi, il rango di P è al più n. Il massimo dei ranghi di tutti gli ideali primi è la dimensione di Krull di R. La dimensione di Krull sale dai casi più semplici a quelli più interessanti. Per gli anelli noetheriani, se la dimensione di Krull è 0 siamo nel caso artiniano, se la dimensione di Krull è 1 siamo essenzialmente nel contesto della teoria dei numeri algebrici. In relazione alla geometria algebrica, la dimensione di Krull corrisponde alla dimensione della varietà.

Bibliografia

Albert 1939: Albert, Abraham A., Structure of algebras, New York, American Mathematical Society, 1939.

Bass 1968: Bass, Hyman, Algebraic K-theory, New York, Benjamin,1968.

Birkhoff 1940: Birkhoff, Garrett, Lattice theory, New York, American Mathematical Society, 1940.

Bourbaki 1939ss.: Bourbaki, Nicolas, Éléments de mathématique, Paris, Hermann, 1939ss.

Burnside 1911: Burnside, William, Theory of groups of finite order, 2. ed., Cambridge, Cambridge University Press, 1911.

Cartan, Eilenberg 1956: Cartan, Henri - Eilenberg, Samuel, Homological algebra, Princeton, Princeton University Press, 1956.

Chevalley 1956: Chevalley, Claude, Fundamental concepts of algebra, New York, Academic Press, 1956 (trad. it.: Concetti fondamentali di algebra, Milano, Feltrinelli, 1964).

Clifford, Preston 1961-1967: Clifford, Alfred H. - Preston, Gordon B., The algebraic theory of semigroups, Providence, American Mathematical Society, 1961-1967.

Fuchs 1970-1973: Fuchs, László, Infinite abelian groups, New York-London, Academic Press, 1970-1973, 2 v.

Gauss 1801: Gauss, Carl Friedrich, Disquisitiones arithmeticae, Lipsiae, 1801.

Grothendieck, Dieudonné 1971: Grothendieck, Alexandre - Dieudonné, Jean A., Éléments de géométrie algébrique, Berlin, Springer, 1971.

Jacobson 1956: Jacobson, Nathan, Structure of rings, Provid-ence, American Mathematical Society, 1956.

Jacobson 1962: Jacobson, Nathan, Lie algebras, New York-London, Interscience, 1962.

Jacobson 1968: Jacobson, Nathan, Structure and representations of Jordan algebras, Providence, American Mathematical Society, 1968.

Lang 1965: Lang, Serge, Algebra, Reading (Mass.), Addison-Wesley, 1965.

MacLane 1971: MacLane, Saunders, Categories for the working mathematician, New York, Springer, 1971.

MacLane, Birkhoff 1967: MacLane, Saunders - Birkhoff, Garrett, Algebra, New York-London, Macmillan, 1967.

Nagata 1962: Nagata, Masayoshi, Local rings, New York-London, Interscience, 1962.

Passman 1971: Passman, Donald S., Infinite group rings, New York, Dekker, 1971.

Sweedler 1969: Sweedler, Moss E., Hopf algebras, New York, Benjamin, 1969.

Van der Waerden 1930-1931: van der Waerden, Bartel L., Moderne Algebra, Berlin, Springer, 1930-1931, 2 v.

Von Neumann, Morgenstern 1953: von Neumann, John - Morgenstern, Oskar, Theory of games and economic behavior, 3. ed., Princeton, Princeton University Press, 1953.

Zariski, Samuel 1958-1960: Zariski, Oscar - Samuel, Pierre, Commutative algebra, Princeton-London, Van Nostrand, 1958-1960, 2 v.