apotema
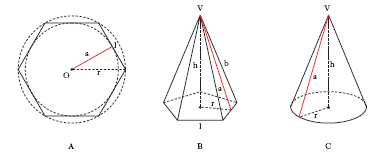
In un poligono regolare (fig. A) di lato l (iscritto in un cerchio di centro O e raggio r), a. è il segmento di perpendicolare condotto da O a un lato; è anche il raggio del cerchio iscritto nel poligono stesso. Indicando con a l’a., si ha dunque:
In una piramide regolare (fig. B), a. è il segmento a di perpendicolare condotto dal vertice V a un lato del poligono di base, cioè l’altezza di una faccia laterale; in tal caso, è a2 = b2−l2/4 o anche a2 = h2+r2, dove b è la lunghezza dello spigolo e l è il lato del poligono di base e h l’altezza della piramide. In un cono circolare retto (fig. C) a. è il segmento a di generatrice compreso tra il vertice V e un punto della circonferenza di base: per il teorema di Pitagora si ha: a2 = h2+r2, dove h è l’altezza e r in tal caso il raggio del cerchio di base.