cubica, curva
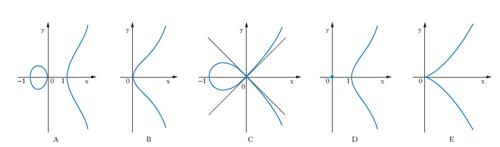
Curva algebrica di ordine 3°. Le c. si distinguono in piane e gobbe. C. piana Ogni curva piana rappresentata in coordinate cartesiane da un’equazione c. in due variabili: f (x, y)=0, dove f (x, y) è un polinomio di 3° grado in x e y. Si deve a I. Newton l’osservazione che le c. piane (v. .) si possono ridurre per proiezione (per umbras) a cinque tipi, e cioè: la parabola campaniforme con ovale, la parabola pura campaniforme, la parabola nodata, la parabola puntata, la parabola cuspidata, tutte rappresentate in fig., sequenzialmente da A a E. Nella fig. Dil punto x=y=0 fa parte della curva come punto isolato, mentre le curve delle fig. C ed E sono dotate rispettivamente di un nodo e di una cuspide. La c. piana senza punto doppio (fig. A e B) è di classe 6 (per un punto del suo piano passano 6 rette, non tutte reali, tangenti alla curva), ed è dotata di 9 flessi, che formano una configurazione interessante: su ogni retta che contenga due flessi si trova un terzo flesso. Da un punto di una c. priva di punto doppio escono quattro rette tangenti altrove alla cubica. Il loro birapporto è costante al variare del punto sulla curva (teorema di Salmon) e si dice modulo della curva. Mentre una c. con punto doppio è razionale (si può rappresentare parametricamente mediante funzioni razionali), una c. senza punto doppio è una curva di genere 1 o ellittica (si può rappresentare parametricamente mediante funzioni ellittiche). C. gobba Curva algebrica spaziale del 3° ordine (ogni piano la incontra in tre punti). La si può sempre pensare come l’intersezione residua di due coni aventi una generatrice in comune. Per ogni punto dello spazio passa una corda e una soltanto della c. gobba: la sua proiezione da un punto su un piano è perciò una c. dotata di punto doppio essendo la c. gobba razionale. Equazione cubica È l’equazione di 3° grado in una incognita, ax3+bx2+cx+d=0.