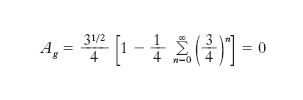gasket
In inglese, intreccio. In matematica g. di Sierpinski, uno dei più semplici esempi di struttura autosomigliante; è costituito a partire da un triangolo equilatero di lato unitario, escludendo la regione contenuta nel triangolo equilatero di lato 1/2 risultante dalla congiunzione dei punti medi dei lati e ripetendo iterativamente la stessa costruzione per ognuno dei triangoli equilateri che si vengono a formare (v. fig.). Sottraendo all’area del triangolo originario le aree dei triangoli successivamente eliminati, si ottiene che l’area Ag della figura rimanente, che è appunto il g. di Sierpinski, è data da
Si può dimostrare che il g. contiene un numero di punti della potenza del continuo e che la sua dimensione di Hausdorff è dH=log3/log2.