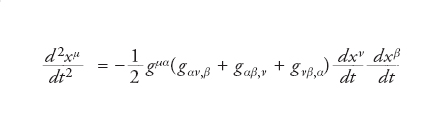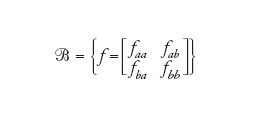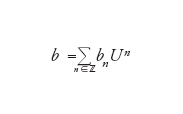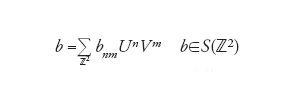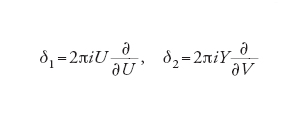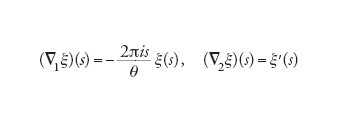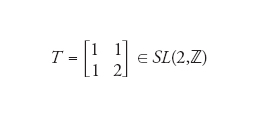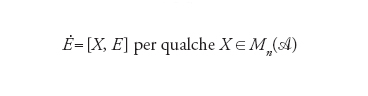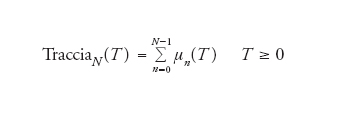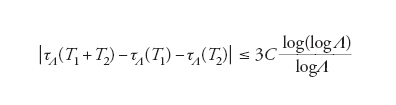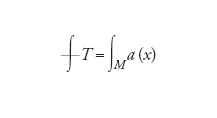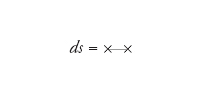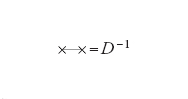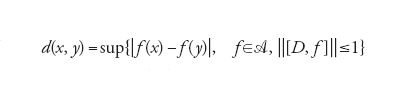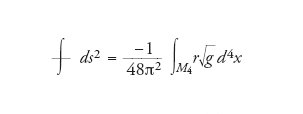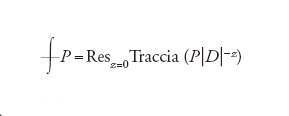Geometria non commutativa

Geometria non commutativa

Se si pensa che la geometria sia strettamente legata al nostro modello di spazio-tempo allora la teoria generale della relatività dà chiaramente ragione a Carl F. Gauss e Georg F. Bernhard Riemann, che presero in considerazione curvature variabili. Essi formularono la geometria intrinseca di uno spazio curvo indipendentemente dall'immersione in uno spazio euclideo. Le due nozioni chiave sono quella di varietà di dimensione arbitraria, i cui punti sono rappresentati da un numero finito di numeri reali x^μ, e quella di elemento lineare, cioè l'unità di lunghezza infinitesimale che permette di misurare le distanze. Il calcolo infinitesimale consente di codificare la geometria mediante la formula dell'elemento lineare ds in termini locali

ds² = g_μνdx^μdx^ν

e di generalizzare la maggior parte dei concetti della geometria euclidea e non euclidea, aumentando considerevolmente il numero di esempi interessanti a disposizione. In particolare, l'idea di linea retta continua ad avere senso ed è data dall'equazione delle geodetiche

[2] formula,

che applicata nella metrica lorentziana di Hermann Minkowski

[3] dx²+dy²+dz²−[1+2V(x, y, z)]dt²

fornisce la legge di Newton per il moto nel campo gravitazionale dovuto alla funzione potenziale V.

Nelle sue lezioni sui fondamenti della geometria, Riemann fu abbastanza cauto da mettere in dubbio la validità della propria ipotesi nell'infinitamente piccolo, proponendo esplicitamente di "modificare gradualmente i fondamenti sotto la spinta di fatti che questi non possono spiegare" nel caso la fisica scoprisse nuovi fenomeni nelle ricerche su piccola scala.

Le origini della geometria non commutativa risalgono appunto alla scoperta di fenomeni di questo genere nello spazio delle fasi del microscopico sistema meccanico che descrive un atomo. Questo sistema si manifesta mediante l'interazione con la radiazione, e le leggi fondamentali della spettroscopia, come scoprirono Walter Ritz e Johannes R. Rydberg, sono in contraddizione con l'immagine di varietà dello spazio delle fasi.

Come risulta direttamente dalle scoperte della spettroscopia ed è stato messo in luce da Werner Heisenberg (e in seguito spiegato a un livello più matematico da Max Born, e altri), quando si ha a che fare con una varietà se ne possono parametrizzare (localmente) i punti x mediante numeri reali x₁,x₂,… che descrivono completamente lo stato del sistema, mentre se si considera lo spazio delle fasi di un sistema meccanico microscopico, anche del tipo più semplice, le coordinate, ovvero i numeri reali x₁,x₂,… che si vorrebbero usare per parametrizzare i punti, non commutano. Ciò significa che il quadro geometrico classico è troppo limitato per poter fornire una descrizione fedele di molti spazi fisici di grande interesse. Ciò che la scoperta di Heisenberg ha mostrato è che la familiare dualità della geometria algebrica tra uno spazio e la sua algebra delle coordinate (cioè l'algebra delle funzioni su questo spazio) è troppo restrittiva per poter descrivere lo spazio delle fasi di un sistema fisico microscopico. L'idea di base è allora quella di estendere questa dualità in modo da non richiedere più che l'algebra delle coordinate su uno spazio sia commutativa.

Nella geometria non commutativa la consueta nozione di varietà formata da punti individuati da coordinate è sostituita da spazi di natura più generale. L'usuale geometria è solo un caso particolare di questa nuova teoria, così come le geometrie euclidea e non euclidea sono casi particolari della geometria riemanniana. Molti dei concetti più familiari continuano a sussistere, ma con un nuovo inatteso significato. Prima di descrivere la nuova nozione di spazio è opportuno spiegare in termini semplici come la geometria non commutativa modifichi la misura delle distanze. Se una spiegazione semplice è possibile, ciò è dovuto al fatto che il passaggio dal modo riemanniano di misurare le distanze al nuovo (non commutativo) corrisponde esattamente a un perfezionamento dello standard di lunghezza del sistema metrico.

Concetto di metrica e nozione di spazio su un'algebra non commutativa

La definizione originale di metro alla fine del XVIII sec. era basata su una parte molto piccola (un quarantamilionesimo) della lunghezza del più grande oggetto macroscopico a disposizione (la circonferenza terrestre). Questa unità di lunghezza ha avuto anche una rappresentazione concreta nel 1799, come mètre des archives, in una sbarra di platino conservata nel Museo di Sèvres presso Parigi. Il prototipo internazionale fu poi sostituito da una copia più stabile del mètre des archives che serviva a definire il metro.

Il cambiamento più drastico nella definizione del metro è avvenuto nel 1960, quando è stato ridefinito come multiplo della lunghezza d'onda di una certa linea spettrale color arancione della luce emessa dall'isotopo 86 del krypton. Questa definizione è stata infine sostituita nel 1983 da quella attuale. Utilizzando la velocità della luce come fattore di conversione, essa si esprime in termini di frequenze inverse piuttosto che di lunghezze d'onda ed è basata su una transizione iperfine nell'atomo di cesio. I vantaggi del nuovo standard sono ovvi. Non sono necessari confronti con alcun mètre des archives, la precisione è dell'ordine di 10⁻¹⁵ e per la maggior parte delle applicazioni un raggio di cesio di tipo commerciale è sufficientemente preciso. Potremmo anche, se una qualche forma di comunicazione fosse possibile, trasmettere la nostra scelta di unità di lunghezza a esseri extraterrestri e uniformare le unità di lunghezza nella galassia senza dover inviare copie concrete del mètre des archives!

Il concetto di metrica nella geometria non commutativa si basa precisamente su un dato spettrale di questo tipo.

Veniamo agli spazi. Vi sono numerosi esempi di spazi con un ovvio significato geometrico che si descrivono meglio con un'algebra delle coordinate non commutativa. Il primo è dato dallo spazio delle fasi della meccanica quantistica ma ve ne sono molti altri: come lo spazio delle foglie delle foliazioni, i duali dei gruppi discreti non abeliani, lo spazio delle tassellazioni di Penrose, il toro non commutativo (che gioca un ruolo nella compattificazione della M-teoria), la zona di Brillouin nella fisica dello stato solido, lo spazio soggiacente ai gruppi quantici ottenuti come deformazioni dei gruppi classici di Lie e infine lo spazio delle classi di adeli, uno spazio geometrico naturale con un'azione del gruppo di scaling che fornisce un'interpretazione spettrale degli zeri delle L-funzioni della teoria dei numeri e una delle formule esplicite di Riemann come formule di traccia.

Il secondo ingrediente fondamentale della teoria è l'estensione delle idee geometriche all'ambito non commutativo, un'estensione che obbliga a riconsiderare la maggior parte delle nozioni a noi familiari. Non basta però aggiungere arbitrariamente l'aggettivo 'quantico' al nostro consueto linguaggio geometrico; la difficoltà sta nello sviluppare estensioni di concetti classici che siano di vasta portata. Questo obiettivo è stato raggiunto in modo più o meno completo per la teoria della misura, la topologia, la geometria differenziale e la geometria riemanniana.

Il principio fondamentale che permette di stabilire la dualità generale è il seguente:

[4] spazi quoziente → algebra non commutativa.

In effetti, molti degli spazi che siamo soliti considerare non sono definiti elencandone i punti ma sono ottenuti per mezzo di identificazioni: i loro elementi sono classi di equivalenza in spazi più grandi. Esistono due modi di procedere a livello algebrico per identificare due punti a e b di un dato spazio M. Il primo consiste nel considerare solo le funzioni definite su M che assumono lo stesso valore nei due punti, cioè tali che f(a)=f(b), e infatti l'usuale algebra delle funzioni associata allo spazio quoziente è

[5] A={f tali che f(a)=f(b)}.

Vi è tuttavia un altro modo per effettuare algebricamente l'operazione di quoziente, che non consiste nel prendere la sottoalgebra data dalla [5] ma nell'aggiungere all'algebra delle funzioni l'identificazione di a e b. L'algebra che si ottiene, ristretta a M={a,b}, è quella delle matrici 2×2:

[6] formula.

In altre parole, non richiediamo che due funzioni abbiano lo stesso valore su a e b; i due punti sono però in relazione tramite gli elementi f_ab e f_ba che si trovano fuori dalla diagonale. L'effetto di tali elementi della matrice consiste nell'identificare questi due punti in un punto dello spettro dell'algebra, cioè nello spazio delle rappresentazioni irriducibili. La rappresentazione irriducibile corrispondente ad a (associata allo stato puro a) è ora divenuta equivalente alla rappresentazione derivante da b. L'equivalenza tra A e ℬ prende il nome di equivalenza di Morita e significa che le corrispondenti categorie di moduli destri sono equivalenti. Vi è naturalmente un'ovvia differenza tra A e ℬ, in quanto al contrario di A l'algebra ℬ non è commutativa.

Diamo un altro semplice esempio; in questo caso i due modi di operare non forniscono lo stesso risultato, neanche a meno dell'equivalenza di Morita. Prendiamo due intervalli [0,1] e identifichiamo i loro punti interni ma non i loro estremi. Applicando il primo procedimento descritto sopra e lavorando nella categoria liscia (C^∞), otteniamo l'algebra di funzioni lisce su M=[0,1]×{0,1} che assumono lo stesso valore nei punti (x,0) e (x,1) per ogni x nell'intervallo aperto (0,1). Ma per continuità funzioni che coincidono all'interno di un intervallo sono uguali anche agli estremi. Ciò che allora si trova è semplicemente l'algebra A=C^∞([0,1]) delle funzioni infinitamente derivabili sull'intervallo [0,1] il cui spettro è l'intervallo [0,1]: non siamo riusciti a tenere distinti i punti estremi. Con il secondo procedimento si costruisce l'algebra delle applicazioni lisce dall'intervallo [0,1] alle matrici 2×2; tuttavia, poiché i punti estremi non vengono identificati, otteniamo soltanto applicazioni lisce che hanno matrici diagonali come valori al contorno. L'algebra ℬ così ottenuta è piuttosto interessante: è l'anello di gruppo liscio del gruppo diedrale, cioè del prodotto libero di due gruppi di ordine 2. Quest'algebra è molto diversa dalla precedente e certamente non è Morita equivalente a C^∞([0,1]).

In generale, quando consideriamo spazi quoziente arbitrari le due algebre A e ℬ non sono Morita equivalenti. La prima operazione ([5]) ha un sapore coomologico, mentre la seconda ([6]) è più vicina allo spazio quoziente.

Descriveremo ora un esempio concreto fondamentale, il toro non commutativo, la cui geometria differenziale non commutativa è stata messa in luce da Alain Connes nel 1980. L'esempio è il seguente. Sia dato il 2-toro

[7] M = ℝ²/ℤ²

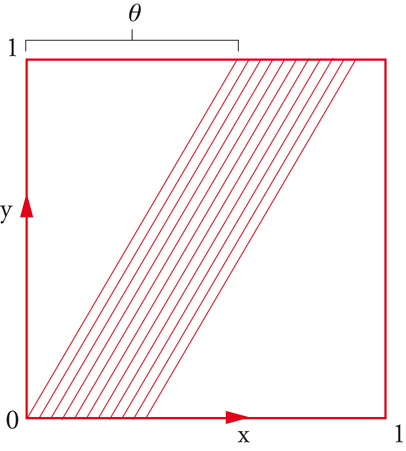
lo spazio X che prendiamo in considerazione è quello delle soluzioni della equazione differenziale

[8] dx = θdy x,y∈ℝ/ℤ

fig. 1

dove θ∈(0,1) è un fissato numero irrazionale (fig. 1).

Siamo pertanto interessati alla foliazione definita dall'equazione differenziale [8]. Possiamo etichettare ciascuna delle foglie con un punto della trasversale data da y=0; otteniamo così il cerchio S¹=ℝ/ℤ. È chiaro che due punti della trasversale che differiscono per un multiplo intero di θ dànno luogo alla stessa foglia e quindi

[9] X = S¹/θℤ

ovvero X è il quoziente di S¹ secondo la relazione di equivalenza che identifica i punti dell'orbita della rotazione irrazionale:

[10] R_θx = x + θ mod 1.

S¹, come spazio in diverse categorie (liscia, topologica, misurabile), è perfettamente descritto dalla corrispondente algebra di funzioni:

[11] C^∞(S¹)⊂C(S¹)⊂L^∞(S¹).

Applicando l'operazione [5] di passaggio al quoziente si ottiene, indipendentemente dalla categoria considerata, il risultato banale

[12] A= ℂ.

L'operazione [6] fornisce invece algebre molto interessanti e non Morita equivalenti a ℂ: nella situazione precedente di un quoziente rispetto all'azione di un gruppo, essa si riduce alla costruzione del prodotto crociato che gli algebristi conoscono dalla teoria delle algebre semplici centrali.

Un elemento b di ℬ è definito da una serie di potenze

[13] formula

dove i b_n sono elementi dell'algebra [11] e la moltiplicazione è definita da:

[14] UhU⁻¹ = h∙R_θ⁻¹.

Ora, l'algebra [11] è generata dalla funzione

[15] V(α) = exp(2πiα) α∈S¹

e dunque ℬ ammette il sistema di generatori (U,V) e una presentazione data dalla relazione

[16] UVU⁻¹ = λ⁻¹V λ=exp(2πiθ).

Quindi, se per esempio ci troviamo nella categoria liscia, un elemento generico b di ℬ è dato da una serie di potenze

[17] formula

dove S(ℤ²) è lo spazio di Schwarz delle successioni rapidamente convergenti su ℤ².

Quest'algebra ha una struttura molto ricca e interessante. È associata alla foliazione [8] (canonicamente, a meno di un'equivalenza di Morita) e l'interazione tra la geometria della foliazione e la struttura algebrica di ℬ comincia osservando che a una trasversale chiusa della foliazione stessa corrisponde canonicamente un modulo proiettivo finito su ℬ. Dalla trasversale x=0 si ottiene il seguente modulo destro su ℬ. Lo spazio soggiacente è l'usuale spazio di Schwarz

[18] S(ℝ)={ξ, ξ(s)∈ℂ ∀s∈ℝ}

delle funzioni lisce sulla retta reale le cui derivate sono rapidamente convergenti. La struttura di modulo destro è data dall'azione dei generatori U,V:

[19] (ξU)(s)=ξ(s+θ), (ξV)(s)=e^πisξ(s) ∀s∈ℝ.

La [16] è soddisfatta ed è interessante che, come modulo destro su ℬ, lo spazio S(ℝ) sia finitamente generato e proiettivo (addendo diretto di un modulo libero). Esso possiede pertanto le proprietà algebriche necessarie per essere chiamato fibrato vettoriale non commutativo secondo il dizionario:

spazio                                       algebra

fibrato vettoriale                      modulo proiettivo finito.

La descrizione concreta di un generico modulo proiettivo finito su A_θ si ottiene mettendo insieme i risultati di Connes (1980), Mihai Pimsner e Dan-Virgil Voiculescu (1980) e Marc A. Rieffel (1983). Questi moduli sono classificati, a meno di isomorfismi, da coppie di interi (p,q) tali che p+qθ≥0 e i moduli corrispondenti H^θ_p,q si ottengono, con la costruzione descritta sopra, dalle trasversali date dalle geodetiche chiuse del toro M.

La controparte algebrica di un fibrato vettoriale è lo spazio delle sezioni lisce C^∞(X,E); in particolare se ne può calcolare la dimensione determinando la traccia dell'endomorfismo identico di E. Applicando questo metodo allo spazio S non commutativo definito dalle [18] e [19], si ottiene:

[20] dim_B(S)=θ.

La comparsa di dimensioni non intere è molto stimolante e mostra un aspetto fondamentale delle algebre di von Neumann di tipo II. La dimensione di un fibrato vettoriale è il solo invariante che resta dal punto di vista della teoria della misura (ossia considerando la terza algebra in [11]). L'algebra di von Neumann che descrive lo spazio quoziente X dal punto di vista della teoria della misura è il prodotto incrociato

[21] R=L^∞(S¹)×∣_Rθℤ

ed è il ben noto fattore iperfinito di tipo II₁. In particolare si ottiene la classificazione dei moduli proiettivi finiti su R mediante un numero reale positivo, la dimensione di Murray e von Neumann:

[22] dim_R(E)∈ℝ₊.

Inoltre, anche se la dimensione del modulo E è irrazionale, quando si calcola l'analogo della prima classe di Chern, cioè dell'integrale della curvatura del fibrato vettoriale, si ottiene un intero. In effetti, i due campi vettoriali commutabili che generano lo spazio tangente per un 2-toro ordinario (commutativo) corrispondono algebricamente a due derivazioni commutabili dell'algebra delle funzioni lisce. Queste derivazioni continuano ad avere senso quando i generatori U e V di C^∞(T²) non sono più commutabili ma soddisfano la [16], generando pertanto C^∞(T_θ²). Sono date dalle stesse formule del caso commutativo:

[23] formula

per cui δ₁(∑b_nmUⁿV^m)=2πi ∑nb_nmUⁿV^m e analogamente per δ₂. Naturalmente si ha ancora

[24] δ₁δ₂=δ₂δ₁

e le δ_j sono ancora derivazioni dell'algebra ℬ=C^∞(T²_θ):

[25] δ_j(bb′)=δ_j(b)b′+bδ_j(b′) ∀b, b′∈ℬ.

Le nozioni analoghe a quelle di connessione e curvatura dei fibrati vettoriali si ottengono facilmente, in quanto una connessione è data semplicemente dalla differenziazione covariante ∇ sullo spazio delle sezioni lisce. Nel caso specifico tale connessione è definita da una coppia di operatori lineari

[26] ∇_j: S(ℝ)→S(ℝ)

tale che

[27] ∇_j(ξb)=(∇_jξ)b+ξ∇_j(b) ∀ξ∈S, b∈ℬ.

Si vede che, come nel caso consueto, la traccia della curvaturaΩ=∇₁∇₂−∇₂∇₁ è indipendente dalla scelta della connessione. Ora, il fatto notevole è che (a meno di opportune potenze di 2πi) la curvatura integrale di S è un intero. Infatti, per la seguente scelta della connessione la curvatura Ω è costante e uguale a 1/θ, per cui il numero irrazionale θ scompare nella curvatura integrale θ×1/θ:

[28] formula.

I valori interi potrebbero dare l'impressione errata che l'algebra ℬ=C^∞(T²_θ) assomigli all'algebra C^∞(T²) delle funzioni lisce sul 2-toro. Considerando però il codominio delle funzioni di Morse si rileva una netta differenza. Il codominio di una funzione di Morse su T² è ovviamente un intervallo connesso mentre il toro non commutativo T²_θ è lo spettro di una funzione reale tale che

[29] h=U+U*+μ(V+V*)

e può essere un insieme di Cantor, cioè può essere totalmente sconnesso. Ciò dimostra che le ombre 1-dimensionali dello spazio T²_θ sono effettivamente differenti dal caso commutativo.

Il toro non commutativo T²_θ appena descritto costituisce l'esempio più semplice di varietà non commutativa e si presenta naturalmente non soltanto nel caso delle foliazioni, ma anche in quello della zona di Brillouin nell'effetto Hall quantizzato, come ha osservato Jean Bellissard. Nella M-teoria, poi, tanto i tori non commutativi quanto le componenti ∇_j delle connessioni di Yang-Mills intervengono in modo naturale nella classificazione degli stati BPS. Nella sua formulazione matriciale infatti le equazioni fondamentali relative alla periodicità di due fra le coordinate X_j sono le seguenti:

[30] U_iX_jU_i⁻¹=X_j+aδ_i^j i=1,2

dove le U_i sono trasformazioni di gauge unitarie.

Il commutatore moltiplicativo U₁U₂U₁⁻¹U₂⁻¹ è quindi centrale e nel caso irriducibile il suo valore scalare λ=exp(2πiθ) fa intervenire l'algebra delle coordinate sul toro non commutativo. Le X_j sono allora le componenti delle connessioni di Yang-Mills. È notevole che lo stesso quadro si sia presentato a partire da altre informazioni che si hanno sulla M-teoria e che riguardano la relazione con la supergravità 11-dimensionale, e altresì che la dualità della teoria delle stringhe si possa interpretare usando l'equivalenza di Morita. Quest'ultima collega i valori di θ su un'orbita di SL(2,ℤ); una relazione di questo tipo, che dal punto di vista delle foliazioni è ovvia, non risulterebbe in uno sviluppo perturbativo (secondo la teoria delle deformazioni) come quello dato dal prodotto di Moyal.

Torneremo più avanti tanto sullo spazio dei moduli naturale per i tori non commutativi quanto sull'aspetto metrico. Dobbiamo però prima fugare l'impressione che il toro non commutativo, per via della sua ubiquità, costituisca l'unico esempio di spazio non commutativo.

Una classe molto ampia di spazi non commutativi è data innanzi tutto dai duali dei gruppi discreti. Ne abbiamo già visto uno, molto semplice, il duale del gruppo diedrale. Non appena si considerino però gruppi discreti più complessi si nota che i loro duali sono precisamente come lo spazio delle foglie delle foliazioni. È importante comprendere, almeno in un caso specifico, perché il duale di un gruppo discreto non abeliano sia essenzialmente uno spazio quoziente come quello che abbiamo già esaminato. A questo scopo sia Γ il gruppo risolubile Γ=ℤ²×∣_αℤ, ottenuto come prodotto semidiretto del gruppo additivo ℤ² con l'azione di ℤ definita dalla matrice

[31] formula.

Per la teoria di Mackey delle rappresentazioni indotte, ogni elemento x del 2-toro ℤ², che è il duale di Pontrjagin del gruppo ℤ², determina per induzione una rappresentazione irriducibile di Γ,

[32] π_x ∈ Irrep(Γ).

Inoltre, le due rappresentazioni π_x e π_y associate ax,y ∈ℤ‸² sono equivalenti se e solo se x e y sono sulla stessa orbita della trasformazione T (trasposta) di ℤ‸². In questo modo non si ottengono tutte le rappresentazioni irriducibili di Γ, ma lo spazio quoziente

[33] formula

corrisponde, nel senso detto sopra, all'anello di gruppo liscio di Γ. Un elenco più completo di altri casi fondamentali è il seguente: (a) spazio delle foglie di una foliazione, (b) spazio delle rappresentazioni irriducibili dei gruppi discreti, (c) spazio delle tassellazioni di Penrose del piano, (d) zona di Brillouin nell'effetto Hall quantistico, (e) spazio delle fasi nella meccanica quantistica, (f) spazio-tempo.

Un'altra classe molto ricca di spazi non commutativi è offerta dalla teoria della deformazione, come per esempio la deformazione delle varietà di Poisson, i gruppi quantistici e i loro spazi omogenei.

Menzioniamo infine lo spazio delle classi di adeli, uno spazio non commutativo la cui comprensione è strettamente legata alla capacità di localizzare gli zeri delle L-funzioni di Hecke nel caso di un campo di numeri.

Non mancano quindi esempi di spazi non commutativi che richiamano la nostra attenzione, ma che sono molto difficili da capire.

Teoria della misura e topologia

Anche a un livello molto grossolano di teoria della misura il caso generale non commutativo non è affatto banale. Se si guarda a uno spazio ordinario e si fa teoria della misura ci si basa sulla teoria molto suggestiva di Henri-Leon Lebesgue, per la quale però tutti gli spazi sono uguali: riguardo alla classificazione non succede nulla. Al contrario, ciò che accade nella teoria della misura non commutativa è molto sorprendente. È interessante scoprire che, quando si considera un'algebra non commutativa M dal punto di vista della teoria della misura, essa evolve con il tempo, ossia ammette un'evoluzione temporale data da un omomorfismo canonico di gruppi

[34] δ: ℝ→Out(M)=Aut(M)/Int(M)

dal gruppo additivo dei reali al centro del gruppo delle classi di automorfismi di M modulo gli automorfismi interni.

Questo omomorfismo è dovuto all'unicità del gruppo di automorfismi modulari di uno stato, a priori dipendente dallo stato stesso. Assieme a precedenti lavori di Robert Powers, Huzihiro Araki, E.J. Woods e Wolfgang Krieger, esso ha dato inizio a una lunga storia che alla fine ha portato alla classificazione completa dei fattori approssimativamente di dimensione finita (detti anche iperfiniti). Tali fattori sono classificati in base al loro modulo

[35] Mod(M)⊂̰ ℝ*₊

che è un sottogruppo chiuso virtuale di ℝ*₊ nel senso di Mackey e cioè un'azione ergodica di ℝ*₊.

Si può interpretare questa classificazione come una teoria di Brauer non banale per campi locali archimedei. La teoria dei campi di classe locale è infatti non banale per campi locali non archimedei come i numeri p-adici, in quanto questi campi sono molto lontani dall'essere algebricamente chiusi: ma non vi è nulla di simile quando la si considera sui numeri complessi, proprio perché il campo complesso è algebricamente chiuso.

La teoria dei fattori è però un sostituto non banale della teoria di Brauer in ambiente archimedeo e ciò può essere osservato nel modo seguente. Si può dimostrare che un campo è algebricamente chiuso in termini di teoria delle rappresentazioni: questo equivale a dire che le rappresentazioni di oggetti semisemplici (gruppi, algebre, ecc.) su questo campo possono essere decomposte nella somma diretta di multipli di rappresentazioni che commutano solo con gli scalari. Naturalmente ciò vale se le rappresentazioni sul campo complesso sono di dimensione finita. Al contrario, se la dimensione è infinita si presenta un nuovo fenomeno, perfettamente analogo a quello delle estensioni non ramificate di campi p-adici. Compaiono fattori non banali, che commutano con le rappresentazioni in uno spazio di Hilbert, e benché il loro centro sia banale non sono Morita equivalenti a ℂ. Tali fattori hanno un invariante, il loro modulo, molto simile al modulo delle algebre semplici centrali su campi locali.

Questo modulo non è propriamente un sottogruppo di ℝ*₊ ma piuttosto un sottogruppo virtuale, nel senso che è un flusso. Tale analogia può essere spinta molto lontano: le varietà non commutative forniscono esempi di costruzione del fattore iperfinito II₁ come prodotto crociato del campo K_q delle funzioni ellittiche per un sottogruppo del suo gruppo di Galois, in perfetta analogia con la teoria di Brauer. La comparsa del fattore di tipo III₁ con semplici costruzioni adeliche offre un'interpretazione spettrale degli zeri delle L-funzioni della teoria dei numeri.

Si può affermare quindi che già la teoria della misura non commutativa non è affatto banale e abbiamo pertanto ragione di credere che andando oltre nella gerarchia naturale delle proprietà di uno spazio si scoprirebbero nuovi fenomeni veramente interessanti.

La teoria della misura rappresenta effettivamente un modo molto grezzo di considerare uno spazio. Immagini sempre più precise si possono ottenere man mano che si sale nella seguente scala: (a) geometria riemanniana, (b) geometria differenziale, (c) topologia, (d) teoria della misura.

Lo sviluppo delle idee topologiche è stato stimolato dai lavori di Izrail M. Gel´fand: le sue algebre C* forniscono il quadro adatto per la topologia non commutativa. Le forze trainanti più importanti sono state la congettura di Novikov sull'invarianza omotopica delle segnature di ordine superiore per varietà ordinarie e il teorema di Atiyah-Singer. Questo sviluppo ha portato alla scoperta che non solo la K-teoria di Atiyah-Hirzebruch, ma, ciò che è ancora più importante, anche la K-omologia duale ammettono come quadro naturale le tecniche degli spazi di Hilbert e dell'analisi funzionale. I cicli nel gruppo di K-omologia K*(X) di uno spazio compatto X sono dati da rappresentazioni di Fredholm dell'algebra C* delle funzioni continue su X. Lo strumento principale è la K-teoria bivariante di Kasparov. Un esempio fondamentale di algebra C* al quale si applica la teoria è l'anello di gruppo di un gruppo discreto; quindi non è certo opportuno limitarsi ad algebre commutative. Sia A un'algebra C*, e siano K₀(A) e K₁(A) i suoi gruppi di K-teoria. Così K₀(A) è la K-teoria algebrica dell'anello A, e K₁(A) la K-teoria dell'anello A⊗C₀(ℝ)=C₀(ℝ,A). Un morfismo A→B di algebre C* induce omomorfismi di gruppi abeliani K_i(A)→K_i(B). La periodicità di Bott fornisce una successione esatta a sei termini di K-teoria per ogni successione esatta 0→J→A→B→0 di algebre C*, e i K-gruppi che vi compaiono dipendono solo dalle rispettive algebre C*.

I gruppi discreti, i gruppi di Lie, le azioni di gruppi e le foliazioni dànno luogo attraverso le loro algebre di convoluzione a un'algebra C* canonica, e quindi a gruppi di K-teoria. È chiaro il significato analitico di questi ultimi come insiemi di indici di operatori ellittici. Essi sono però difficili da calcolare. Per esempio nel caso dei gruppi di Lie semisemplici K₀C*_r(G), dove C*_r(G) è l'algebra C* ridotta di G, contiene il gruppo abeliano libero con un generatore per ogni rappresentazione irriducibile di serie discrete. Così, in questo caso, una determinazione esplicita della K-teoria comporta una enumerazione delle serie discrete. Assieme a Paul F. Baum abbiamo introdotto una K-teoria definita geometricamente che contempla in particolare gruppi discreti, gruppi di Lie, azioni di gruppi e foliazioni. Le proprietà principali sono la computabilità e la semplicità delle definizioni. Nel caso dei gruppi di Lie semisemplici essa chiarisce il ruolo dello spazio omogeneo G/K (K è il sottogruppo compatto massimale di G) nella costruzione geometrica della serie discreta di Atiyah-Schmid. Usando operatori ellittici abbiamo costruito un'applicazione naturale μ dai nostri gruppi di K-teoria definiti geometricamente ai gruppi di K-teoria analitici (cioè di algebre C*) e negli anni passati sono stati realizzati molti progressi per determinare quando si tratta di un isomorfismo. Tra i contributi più importanti citiamo quelli di Gennadij G. Kasparov e Nigel Higson, i quali hanno dimostrato come l'isomorfismo congetturato sussista per i gruppi amenabili. Sappiamo che questo è il caso anche per gruppi di Lie semisemplici reali, grazie in particolare ai lavori di Antony Wassermann. Inoltre, i lavori recenti di Vincent Lafforgue hanno permesso di superare la barriera della proprietà T, dimostrando l'esistenza dell'isomorfismo per sottogruppi compatti di rango 1 dei gruppi di Lie, e anche di SL(3,ℝ) e di gruppi di Lie p-adici. Lafforgue ha anche fornito la prima dimostrazione concettuale dell'isomorfismo per i gruppi di Lie semisemplici reali o p-adici. Il risultato per tutti i gruppi connessi e localmente compatti, basato sui lavori di Lafforgue, è dovuto a Jerome Chabert, Siegfried Echterhoff e Ryszard Nest. La dimostrazione di Guaoliang Yu dell'analogo della congettura (dovuta a John Roe) nel contesto della geometria coarse per spazi metrici immergibili uniformemente in uno spazio di Hilbert, e il lavoro di George Skandalis, Jean-Louis Tu, Roe e Higson nel caso di un gruppoide hanno conseguenze rilevanti come l'iniettività dell'applicazione μ per una C*_r(Γ) esatta, dimostrata da Jerome Kaminker, Erik Guentner e Narutaka Ozawa. Infine, i risultati ottenuti indipendentemente da Lafforgue da un lato e Igor Mineyev e Yu dall'altro mostrano che la congettura è vera per gruppi iperbolici arbitrari (la maggior parte dei quali hanno la proprietà T). Pierre Julg ha potuto anche dimostrare la congettura con coefficienti per gruppi di rango 1, a tutt'oggi probabilmente il risultato positivo più importante. La possibile estensione a gruppi iperbolici arbitrari è oggetto di intense ricerche. Sul versante negativo, sviluppi recenti dovuti a Misha Gromov, Higson, Lafforgue e Skandalis indicano controesempi alla congettura generale per gruppoidi localmente compatti, basati sul fatto che il funtore G→K₀(C*_r(G)) non è semiesatto contrariamente al funtore dato dal gruppo geometrico. Ciò rende davvero interessante il problema generale di calcolare K₀(C*_r(G)) e mostra come, oltre a determinare la vasta classe di gruppi localmente compatti per i quali la congettura originale è vera, occorra far entrare in gioco l'algebra omologica per definire la corretta formulazione generale.

Idee di geometria differenziale, comprese l'omologia di de Rham, le connessioni e la curvatura di fibrati vettoriali, ecc., sono state sviluppate durante gli anni Ottanta del Novecento grazie alla coomologia ciclica. Ciò ha consentito la dimostrazione della congettura di Novikov per i gruppi iperbolici, ma si sono avute anche altre applicazioni. Generalizzando il concetto di classi caratteristiche di Chern-Weil, la coomologia ciclica permette molte applicazioni concrete di natura geometrico-differenziale in spazi non commutativi, rivelando anche la profondità della relazione tra la classificazione dei fattori vista sopra e la geometria delle foliazioni. Utilizzando la coomologia ciclica assieme a un seguente semplice lemma secondo il quale

[36]   un gruppo connesso può agire soltanto

banalmente su una teoria coomologica

invariante per omotopia

si dimostra che per ogni foliazione F di codimensione uno su una varietà compatta V con classe di Godbillon-Vey non nulla si ha:

[37] Mod(M) ha covolume finito in ℝ*₊

dove M=L^∞(V,F) e un sottogruppo virtuale di covolume finito è un flusso con una misura invariante finita.

Per comprendere il concetto di coomologia ciclica è bene cominciare con il dimostrare, per esempio, il seguente semplice lemma: sia A un'algebra e φ una forma trilineare su A tale che

[38] φ(a₀, a₁, a₂)=φ(a₁, a₂, a₀) ∀a_j ∈ A

[39] φ(a₀, a₁, a₂, a₃)−φ(a₀, a₁, a₂, a₃)+φ(a₀, a₁, a₂, a₃)−

−φ(a₂, a₀, a₁, a₂)=0 ∀a_j ∈ A.

Allora lo scalare φ_n(E,E,E) è invariante per omotopia per proiettori (idempotenti) E∈M_n(A) (qui φ è stato esteso univocamente a M_n(A) usando la traccia su M_n(ℂ), cioè φ_n=φ⊗Tr).

La dimostrazione non è difficile; il fatto è che una deformazione di idempotenti è sempre isospettrale:

[40] formula.

Quando prendiamo A=C^∞(M) per una varietà M e poniamo

[41] φ(f⁰, f¹, f²)=〈C, f⁰df¹∧df²〉 ∀f^j ∈ A

dove C è una corrente di de Rham chiusa 2-dimensionale, l'invariante φ_n(E,E,E) è uguale (a meno di una normalizzazione) a

[42] 〈C, c₁(E)〉

dove c₁ è la prima classe di Chern del fibrato vettoriale E su M la cui fibra su x∈M è il codominio di E(x)∈M_n(ℂ). In questo esempio, per ogni permutazione di {0,1,2} si ha

[43] φ(f^σ(0), f^σ(1), f^σ(2))=ε(σ)φ(f⁰, f¹, f²)

dove ε(σ) è il segno della permutazione. Tuttavia, estendendo φ a M_n(A) secondo la φ_n=φ⊗Tr,

[44] φ_n(f⁰⊗μ⁰, f¹⊗μ¹, f²⊗μ²)=φ(f⁰, f¹, f²)Tr(μ⁰μ¹μ²)

e la proprietà [41] resta valida solo per permutazioni cicliche. Ciò giustifica il nome di coomologia ciclica dato alla teoria coomologica corrispondente.

Nell'esempio del toro non commutativo, il cociclo ciclico che dà un invariante intero è

[45] φ(b⁰, b¹, b²)=τ(b⁰(δ₁(b¹)δ₂(b²)−δ₂(b¹)δ₁(b²)))

dove τ è la traccia unica

[46] τ(b)=b₀₀ per b= ∑b_nmUⁿW^m.

Il pairing dato dal lemma fornisce allora la conduttività di Hall quando si applica a una proiezione spettrale dell'hamiltoniana.

Otteniamo allora in generale le prime voci di un dizionario che collega le usuali nozioni geometriche alle corrispondenti nozioni algebriche, in modo che queste ultime abbiano senso in una situazione generale non commutativa:

spazio                                                                      algebra

fibrato vettoriale                                            modulo proiettivo finito

forma differenziale                                 (classe del) ciclo di Hochschild

corrente di de Rham                           (classe del) cociclo di Hochschild

coomologia di de Rham                                  coomologia ciclica

teoria di Chern-Weil                                       pairing 〈K(A), HC(A)〉.

Naturalmente un tale dizionario, che traduce nozioni standard di geometria in termini che non fanno intervenire la commutatività, fornisce solo un'idea superficiale della geometria non commutativa. Infatti, come abbiamo già visto per la teoria della misura, ciò che importa non è soltanto tradurre ma scoprire fenomeni completamente nuovi.

Per esempio, la coomologia ciclica, che sostituisce nel caso non commutativo la coomologia di de Rham, non è graduata come quest'ultima bensì filtrata. Inoltre, essa eredita dall'applicazione carattere di Chern un reticolo naturale intero. Questi due aspetti giocano un ruolo fondamentale nella descrizione dello spazio naturale dei moduli (o più precisamente dello spazio di Teichmüller, assieme all'azione naturale di SL(2,ℤ) su questo spazio) per il toro non commutativo T²_θ. La discussione è parallela alla descrizione dello spazio dei moduli delle curve ellittiche, ma fa intervenire la coomologia pari invece di quella dispari.

Le varietà nella geometria non commutativa

Veniamo ora alla nozione centrale della geometria non commutativa, cioè all'individuazione degli analoghi non commutativi dei due concetti fondamentali della formulazione di Riemann della geometria: i concetti di varietà e di elemento infinitesimale di curva. Questi analoghi non commutativi sono entrambi di natura spettrale e si combinano per dar luogo alle nozioni di terna spettrale e di varietà spettrale che descriveremo più avanti.

Ci serviremo della teoria degli operatori per il calcolo di infinitesimali, che fornirà anche il luogo naturale per l'elemento infinitesimale di curva ds.

Lo scenario è quello della meccanica quantistica. Osserviamo le prime due linee del seguente dizionario che traduce nozioni classiche nel linguaggio degli operatori in uno spazio di Hilbert ℋ:

variabile complessa                               operatore in ℋ

variabile reale                                         operatore autoaggiunto

infinitesimo                                              operatore compatto

infinitesimo di ordine α                           operatore compatto con

-autovalori μ_n che soddisfano μ_n=O(n^−α), n→∞

integrale di un                                         ∫_T=coefficiente di divergenza

infinitesimo di ordine 1                           logaritmica nella traccia di T.

Una variabile (in senso intuitivo) va pensata come un operatore in uno spazio di Hilbert. L'insieme dei valori della variabile è lo spettro dell'operatore e il numero di volte in cui un valore viene ottenuto è la molteplicità spettrale. Una variabile reale corrisponde a un operatore autoaggiunto; il suo spettro è reale e si può agire su di esso con una qualunque funzione misurabile. In generale si può agire su una variabile complessa solo con funzioni olomorfe, e ciò è esattamente quanto accade per operatori non autoaggiunti. In questo dizionario sono considerati anche gli infinitesimi, ossia quantità minori di un qualunque numero reale ε positivo e diverse da zero. Se è troppo richiedere che la norma dell'operatore sia infinitesima, si può essere più sottili e postulare che per ogni ε positivo si possano imporre all'operatore un numero finito di condizioni lineari tali che la sua norma risulti minore di ε. È ben noto che ciò caratterizza gli operatori compatti in uno spazio di Hilbert: questi sono allora gli ovvi candidati per gli infinitesimi. Le regole fondamentali degli infinitesimi sono facili da verificare; per esempio, la somma di due operatori compatti è un operatore compatto; il prodotto di un operatore compatto con uno limitato è compatto.

L'ordine dell'infinitesimo T di un ideale K è governato dalla velocità di convergenza della successione decrescente dei suoi autovalori μ_n=μ_n(T), per n→∞. In particolare, per tutti i reali positivi α la seguente condizione definisce infinitesimi di ordine α:

[47] μ_n(T)=O(n^−α) quando n→∞

(esiste cioè C>0 tale che μ_n(T)≤Cn^−α, per ogni n≥1). Gli infinitesimi di ordine α formano anche un ideale bilatero; inoltre

[48] T_j di ordine α_j ⇒ T₁T₂ di ordine α₁+α₂ (j=1,2).

Poiché l'ordine di infinitesimo è misurato dalla successione μ_n→0, può sembrare che si possa fare a meno del formalismo degli operatori e sia sufficiente sostituire l'ideale K in L(ℋ) con l'ideale c₀(ℕ) delle successioni che convergono a zero nell'algebra ℓ^∞(ℕ) delle successioni limitate. Una variabile sarebbe semplicemente una successione limitata e un infinitesimo una successione μ_n,μ_n→0. Tuttavia, questa versione commutativa non ammette l'esistenza di variabili a codominio continuo in quanto gli elementi di ℓ^∞(ℕ) hanno uno spettro puntuale e una misura spettrale discreta. Ciò non è accettabile perché si escluderebbero variabili che hanno uno spettro di Lebesgue. Gli infinitesimi possono coesistere con le variabili continue solo grazie alla non commutatività. La mancanza di commutatività tra l'elemento di curva e le coordinate di uno spazio fornisce la misura delle distanze.

Un altro ingrediente chiave di questo dizionario è l'integrale che si ottiene con la seguente analisi, dovuta principalmente a Jacques Dixmier, della divergenza logaritmica delle tracce parziali:

[49] formula(

è utile definire Traccia_λ(T) per ogni reale positivo λ>0 con una interpolazione affine a tratti per λ non intero).

Definiamo per tutti gli operatori T≥0 di ordine 1

[50] formula

che è la media di Cesaro della funzione Traccia_μ(T)/logμ sul gruppo di scaling R*₊. Per T≥0 infinitesimo di ordine 1 si ha

[51] Traccia_Λ(T)≤ClogΛ ,

per cui τ_λ(T) è limitato. La proprietà fondamentale è la seguente additività asintotica del coefficiente τ_λ(T) della divergenza logaritmica [49]:

[52] formula

per T₁,T₂≥0.

Una conseguenza diretta della [52] è che ogni punto limite τ dei funzionali non lineari τ_λ, per λ→∞, definisce una traccia positiva e lineare sull'ideale bilatero degli infinitesimi di ordine 1.

In pratica, la scelta del punto limite τ è irrilevante perché in tutti gli esempi importanti T è un operatore misurabile e cioè

[53] τ_Λ(T) converge quando Λ→∞.

Il valore τ(T) è allora indipendente dalla scelta del punto limite τ e si denota con ∫_T.

Il primo caso interessante è dato dall'operatore pseudodifferenziale T su una varietà differenziabile M. Se T è di ordine 1 nel senso sopra visto è misurabile e ∫_T è il residuo non commutativo di T, che ha un'espressione locale in termini del nucleo di distribuzione k(x,y), con x,y∈M. Per T di ordine 1, il nucleo k(x,y) diverge logaritmicamente nelle vicinanze della diagonale:

[54] k(x, y)=−a(x)log∣x−y∣+O(1) quando y→x

dove a(x) è una 1-densità indipendente dalla scelta della distanza riemanniana ∣x−y∣. Allora, a meno di normalizzazione, si ha

[55] formula.

Il membro a destra della [55] ha senso per tutti gli operatori pseudodifferenziali; si vede facilmente infatti che il nucleo di un tale operatore è asintoticamente della forma

[56] k(x, y)=∑a_k(x, x−y)−a(x)log∣x−y∣+O(1)

dove a_k(x,ξ) è omogeneo di grado −k in ξ e la 1-densità a(x) è definita intrinsecamente in quanto in un cambiamento locale di coordinate il logaritmo non assume valori razionali.

Lo stesso principio della estensione di ∫_ a infinitesimi di ordine 〈1 funziona per operatori ipoellittici e, più in generale, per terne spettrali il cui spettro dimensionale è semplice.

Con questo strumento a disposizione torniamo ora alle due nozioni fondamentali introdotte da Riemann in ambito classico, quelle di varietà e di elemento lineare. Vedremo che entrambe si adattano perfettamente al caso non commutativo e ciò ci permetterà di definire la nozione di terna spettrale sulla quale si basa la geometria non commutativa. Nella geometria ordinaria, naturalmente, si può ottenere una varietà specificando carte e diffeomorfismi locali. Si potrebbe essere tentati di proporre un metodo analogo nel caso non commutativo, ed è in realtà quanto si ottiene con la costruzione generale delle algebre di foliazioni. Un buon test per ogni idea generale è verificare se essa comprenda almeno quest'ultima classe di esempi.

Tuttavia, a un livello più concettuale, i geometri hanno riconosciuto ormai da tempo che la qualità principale del tipo di omotopia di una varietà orientata è il fatto di soddisfare la dualità di Poincaré, non solo nell'omologia ordinaria ma anche nella K-omologia. La dualità di Poincaré nell'omologia ordinaria non è sufficiente a descrivere il tipo di omotopia delle varietà, ma Dennis Sullivan ha dimostrato (nel caso lineare a tratti semplicemente connesso di dimensione ≥5, non tenendo conto della 2-torsione) che basta sostituire l'ordinaria omologia con la KO-omologia. Inoltre, il carattere di Chern della classe fondamentale di KO-omologia contiene tutte le informazioni razionali sulle classi di Pontrjagin.

La proprietà caratteristica delle varietà differenziabili che si trasporta al caso non commutativo è la dualità di Poincaré nella KO-omologia.

Inoltre, come abbiamo visto discutendo della topologia, la K-omologia ammette una definizione piuttosto semplice in termini di spazi di Hilbert e di rappresentazioni di Fredholm di algebre, così com'è gradualmente emerso dai lavori di Michael F. Atiyah, Isadore Singer, Lawrence G. Brown, Richard G. Douglas, Peter A. Fillmore, Aleksandr S. Mišenko e Gennadij G. Kasparov.

Per una varietà ordinaria la scelta del ciclo fondamentale in una K-omologia è un raffinamento della scelta dell'orientazione della varietà, e nella sua forma più semplice è la scelta di una struttura di spin. Naturalmente il ruolo della struttura di spin è di permettere la costruzione del relativo operatore di Dirac, che fornisce la corrispondente rappresentazione di Fredholm dell'algebra delle funzioni lisce. L'origine della costruzione dell'operatore di Dirac sta nell'estrazione della radice quadrata di un operatore differenziale del secondo ordine come il laplaciano.

Tutto ciò porta non solo alla nozione di varietà non commutativa ma anche alla definizione di una formula, tipica della teoria degli operatori, per l'elemento lineare ds. Nel caso riemanniano si sviluppa in serie di Taylor il quadrato ds² dell'elemento lineare infinitesimale; in una varietà non commutativa l'estrazione di radice effettuata con l'operatore di Dirac ci permette di considerare direttamente ds.

fig. 2

L'unità di lunghezza infinitesimale ds deve essere un infinitesimo nel senso della teoria degli operatori, e un modo per avere un'idea intuitiva della formula che definisce ds è considerare i diagrammi di Feynman che i fisici usano correntemente nei calcoli della teoria quantistica dei campi. Consideriamo il diagramma nella fig. 2, che compare nel calcolo dell'autoenergia di un elettrone nell'elettrodinamica quantistica. I due punti x e y dello spazio-tempo nei quali viene emesso e assorbito il fotone (rappresentato dalla linea curva) sono molto vicini e la definizione di ds è intuitivamente

[57] formula.

Il membro a destra della [57] ha un significato in fisica: si chiama propagatore del fermione ed è dato da

[58] formula

dove D è l'operatore di Dirac. Arriviamo quindi alla relazione fondamentale:

[59] ds=D⁻¹.

In un certo senso la definizione [59] di ds è più semplice di quella espressa dalla [1]; il fatto è che la struttura di spin permette effettivamente di estrarre la radice quadrata di ds².

Innanzitutto è necessario controllare che possiamo ancora misurare le distanze con l'unità di misura ds data dalla [59]. Abbiamo visto infatti, nella discussione del calcolo quantizzato, che variabili con immagine continua non possono commutare con infinitesimi come ds, e non è perciò sorprendente che questa mancanza di commutatività permetta di calcolare, nel caso riemanniano classico, la distanza geodetica d(x,y) tra due punti. Tale distanza è data da

[60] formula

dove D=ds⁻¹ e A è l'algebra delle funzioni lisce. Si osservi che ds ha la dimensione di una lunghezza, D ha la dimensione dell'inversa di una lunghezza e l'espressione [60] per d(x,y) ha anch'essa la dimensione di una lunghezza.

Pertanto, nel caso geometrico classico, sia il ciclo fondamentale nella K-omologia sia la metrica sono codificate nella terna spettrale (A,ℋ,D), dove A è l'algebra delle funzioni che agiscono nello spazio di Hilbert ℋ degli spinori e D è l'operatore di Dirac.

Ci si può familiarizzare con questa nozione verificando che con l'uguaglianza (valida a meno di una costante di normalizzazione)

[61] formula

si ritrovi l'elemento di volume della metrica riemanniana. Il primo punto interessante è che, oltre alla coerenza, con i soliti calcoli vi sono semplici domande che ora possiamo porci. Per esempio: qual è la misura 2-dimensionale di una 4-varietà? In altre parole, qual è la sua area? Occorre quindi calcolare

[62] formula.

È ovvio dalla teoria degli invarianti che l'integrale nella [62] deve essere proporzionale all'azione di Hilbert-Einstein; il calcolo diretto è stato eseguito da Daniel Kastler e dà

[63] formula

dove, come sopra, dv=√_g d⁴x è l'elemento di volume, ds=D⁻¹ l'elemento di lunghezza, cioè l'inverso dell'operatore di Dirac, e r la curvatura scalare.

Terne spettrali e loro proprietà

Nel contesto generale della geometria non commutativa la convergenza delle due nozioni, in forma hilbertiana, di metrica e di classe fondamentale per una varietà porta in modo naturale a definire uno spazio geometrico come dato da una terna spettrale

[64] (A, ℋ, D)

dove A è un'algebra concreta di coordinate rappresentata su uno spazio di Hilbert ℋ e l'operatore D è l'inverso dell'elemento lineare definito dalla [59].

Questa definizione è interamente spettrale: gli elementi dell'algebra sono operatori; i punti, se esistono, provengono dallo spettro degli operatori e l'elemento lineare è un operatore.

Le proprietà fondamentali di queste terne spettrali sono facili da formulare e non fanno intervenire la commutatività dell'algebra A. Esse sono:

[65] [D, a] è limitato per qualunque a∈A,

[66] D=D* e (D+λ)⁻¹ è un operatore compatto ∀λ∉ℝ

(ovviamente D è un operatore non limitato).

Non vi sono difficoltà ad adattare la formula che fornisce la distanza al caso generale non commutativo; si ottiene la stessa espressione, con i punti x e y sostituiti da stati arbitrari φ e ψ sull'algebra A. Ricordiamo che uno stato è una forma lineare positiva normalizzata su A tale che φ(1)=1, ovvero

[67] φ:A→ℂ, φ(a*a)≥0 ∀a∈A, φ(1)=1.

La distanza tra due stati è data da

[68] d(φ, ψ)=sup{∣φ(a)−ψ(a)∣; a∈A, ∣∣[D, a]∣∣≤1}.

Il significato di D è duplice: da un lato definisce la metrica mediante l'equazione [68], dall'altro la sua classe di omotopia rappresenta la classe fondamentale di K-omologia dello spazio in considerazione.

Esiste una formula ugualmente semplice per l'azione di Yang-Mills in generale. L'analogo del funzionale dell'azione di Yang-Mills e la classificazione delle connessioni di Yang-Mills sui tori non commutativi sono stati sviluppati nel 1985 da Connes e da Marc A. Rieffel, con l'obiettivo principale di definire una varietà ombra per questi spazi non commutativi. Tali spazi di moduli si sono rivelati perfettamente adatti allo scopo: essi permettono, per esempio, di ritrovare l'usuale spazio delle classi di gauge-equivalenza di connessioni di Yang-Mills come un invariante della metrica non commutativa.

Come abbiamo osservato all'inizio, il passaggio dal paradigma riemanniano di geometria a quello spettrale visto sopra è sostanzialmente parallelo all'evoluzione dell'unità di lunghezza in fisica. Lo standard di lunghezza attuale è la lunghezza d'onda corrispondente a particolari transizioni nell'atomo di cesio. Le frequenze inverse si calcolano dalla corrispondente hamiltoniana di Dirac in perfetta analogia con la precedente definizione spettrale di ds. L'unità di lunghezza non è più localizzata, per via della mancanza di commutatività con le coordinate dello spazio-tempo.

Esiste un test molto importante per il quadro generale della geometria che abbiamo fornito, ed è la sua compatibilità con ciò che sappiamo dello spazio-tempo. Il modo migliore è cominciare con il nocciolo duro dato dalle informazioni fornite dalla fisica e che possono essere riassunte da una lagrangiana. Questa lagrangiana è quella di Einstein più la lagrangiana del Modello standard con accoppiamento minimale. Come recuperare questo funzionale dell'azione, che contiene sia il termine di Einstein-Hilbert sia il Modello standard? La risposta è molto semplice: la parte fermionica di questa azione si usa per determinare una terna spettrale (A,ℋ,D), dove l'algebra A codifica non soltanto l'ordinario spazio-tempo (definito nella elettrodinamica quantistica) ma anche le simmetrie interne, lo spazio di Hilbert ℋ gli ordinari spinori (definiti anch'essi nella elettrodinamica quantistica) e tutti i quark e i leptoni, e l'operatore D l'ordinario operatore di Dirac e la matrice di accoppiamento di Yukawa. Si recupera poi la parte bosonica come segue. Il funzionale dell'azione di Hilbert-Einstein per la metrica di Riemann, l'azione di Yang-Mills per i potenziali vettoriali, l'autointerazione e l'accoppiamento minimale per i campi di Higgs compaiono tutti con il segno giusto nello sviluppo asintotico, per grandi valori di λ, del numero N(λ) di autovalori di D che sono ≤λ in modulo:

[69] N(Λ)= #autovalori di D in [−Λ, Λ].

Questa funzione a gradini N(λ) è la sovrapposizione di due termini: N(λ)=〈N(λ)〉+N_OSC(λ). La parte oscillatoria N_OSC(λ) è la stessa che per una matrice aleatoria ed è definita dalla statistica dettata dalle simmetrie del sistema; qui non ci riguarda. 〈N(λ)〉 si calcola mediante un'approssimazione semiclassica a partire da espressioni locali nelle quali interviene lo sviluppo consueto dell'equazione del calore e fornisce i termini corretti. Altri termini non nulli nello sviluppo asintotico sono di natura coomologica e dipendono dalla gravità di Weyl e dalla topologia. Abbiamo dimostrato, assieme a Giovanni Landi e Michel Dubois-Violette, che se si studiano rappresentazioni naturali dell'algebra generata da A e D si ottengono soltanto metriche con un fissato elemento di volume, per cui il fastidioso termine coomologico non interviene nelle equazioni variazionali associate all'azione spettrale 〈N(λ)〉. Si è tentati di pensare che la lagrangiana fenomenologica della fisica, che combina materia e gravità, compaia dalla soluzione di una semplicissima equazione della teoria degli operatori.

Nella situazione spettrale non commutativa la nozione di curvatura proviene dal calcolo locale delle analoghe delle classi di Pontrjagin, cioè dalle componenti del cociclo ciclico che è il carattere di Chern della classe di K-omologia di D e che ha senso in generale. Questo risultato permette, usando il calcolo infinitesimale, di passare dal locale al globale nella situazione generale delle terne spettrali (A,ℋ,D).

L'indice di Fredholm dell'operatore D determina (per semplicità consideriamo soltanto il caso dispari, ma vi sono formule simili anche nel caso pari) un'applicazione additiva K₁(A)→^φℤ data dall'uguaglianza

[70] φ([u])=Indice(PuP) u∈GL₁(A),

dove P è il proiettore P=(1+F)/2, F=Segno(D).

È facile vedere che questa applicazione si calcola mediante il pairing di K₁(A) con il seguente cociclo ciclico:

[71] τ(a⁰,…, aⁿ)=Traccia(a⁰[F, a¹]…[F, aⁿ]) ∀a^j∈A

dove F=Segno(D) e supponiamo che la dimensione p del nostro spazio sia finita; ciò significa che (D+i)⁻¹ è di ordine 1/p e che inoltre n≥p è un intero dispari. Vi sono formule simili nelle quali compare la graduazione γ nel caso pari ed è positivo che sia la coomologia ciclica sia la formula dei caratteri di Chern si adattino al caso della dimensione infinita, nel quale la sola ipotesi è che exp(−D²) sia un operatore di traccia.

Il cociclo τ, tuttavia, non è in generale locale perché nella formula [71] compare la traccia ordinaria invece della traccia locale ∫__ cruciale per ottenere una forma locale del detto cociclo. Abbiamo risolto questo problema con Henri Moscovici. Con la seguente ipotesi di regolarità su (A,ℋ,D)

[72] a, [D, a] ∈ ∩Dom(δ^k) ∀a∈A

dove δ è la derivazione δ(T)=[∣D∣,T] per ogni operatore T. Sia ℬ l'algebra generata da δ^k(a) e δ^k([D,a]). L'usuale nozione di dimensione di uno spazio è sostituita da quella di spettro dimensionale, cioè dal sottoinsieme, {z∈ℂ, Re(z)≥0} delle singolarità delle funzioni analitiche

[73] ζ_b(z)=Traccia(b∣D∣^−z) Re(z) > p, b∈ℬ.

Lo spettro dimensionale di un'ordinaria varietà M è l'insieme {0,1,2,…,n}, n=dimM, ed è semplice. Le molteplicità compaiono nel caso di varietà singolari. Gli insiemi di Cantor forniscono esempi di punti complessi z∉ℝ nello spettro dimensionale.

Supponiamo che ∑ sia discreto e semplice. Sia (A,ℋ,D) una terna spettrale che soddisfa le ipotesi [72] e [73]. Il teorema dell'indice locale è il seguente:

(a) L'uguaglianza

[74] formula

definisce una traccia nell'algebra generata da A, [D,A] e ∣D∣^z, dove z∈ℂ.

(b) Vi sono soltanto un numero finito di termini non nulli nella formula seguente, che definisce le componenti dispari (φ_n)_n=1,3,… di un cociclo nel bicomplesso (b,ℬ) di A,

[75] formula

dove si usano le seguenti notazioni: T^(k)=∇^k(T) e ∇(T)=D²T−TD², k è un multi-indice, ∣k∣=k₁+…+k_n,

[76] formula.

(c) Il pairing della classe di coomologia ciclica (φ_n)∈HC*(A) con K₁(A) fornisce l'indice di Fredholm di D con coefficienti in K₁(A).

Il primo test di questa formula generale dell'indice locale è stato il calcolo delle classi locali di Pontrjagin nel caso delle foliazioni. La loro geometria trasversa è codificata da una terna spettrale. La risposta per il caso generale è stata ottenuta grazie a un'algebra di Hopf ℋ(n) dipendente solo dalla codimensione n della foliazione. Essa ha permesso di organizzare il calcolo e di codificare algebricamente la curvatura non commutativa. Ha inoltre dettato anche la corretta generalizzazione della coomologia ciclica per le algebre di Hopf. Un altro caso di grande interesse è stato recentemente suggerito dai gruppi quantici, nei quali la formula locale dell'indice funziona bene e fornisce formule notevoli anche nel casodi SU_q(2), che è quello più semplice.

Pressappoco nello stesso periodo della scoperta di ℋ(n), Dirk Kreimer ha trovato un'altra algebra di Hopf che permette di definire i calcoli di rinormalizzazione nella teoria quantistica dei campi. L'algebra di Kreimer è commutativa; essa è l'algebra di Hopf duale dell'algebra inviluppante di un'algebra di Lie la cui base è indicizzata dai grafi di Feynman 1PI (un grafo di Feynman è una particella irriducibile 1PI se è connesso e lo resta dopo aver soppresso uno qualunque dei suoi spigoli). Il crochet di Lie di due di questi grafi si ottiene inserendo un grafo nell'altro. Il corrispondente gruppo di Lie è quello dei caratteri di ℋ. Abbiamo dimostrato che tale gruppo è il prodotto semidiretto di un gruppo abeliano, di facile comprensione, per un gruppo che invece non è affatto banale e che è strettamente legato a gruppi di diffeomorfismi. Concettualmente, i calcoli concreti effettuati dai fisici nella tecnica di rinormalizzazione sono essenzialmente un caso particolare di un principio generale di estrazione moltiplicativa di valori finiti che ha origine nel problema di Riemann-Hilbert. La decomposizione di Birkhoff è la fattorizzazione

[77] γ(z)=γ₋(z)⁻¹γ₊(z) z∈C

dove C⊂P₁(ℂ) è un curva semplice liscia, C₋ la componente del complementare di C che contiene ∞∉C e C₊ l'altra componente. Sia γ sia γ_± sono cappi a valori in G,

[78] γ(z)∈G ∀z∈ℂ

mentre γ_± sono valori al contorno di applicazioni olomorfe (denotati con lo stesso simbolo):

[79] γ_±:C_±→G.

La condizione di normalizzazione γ₋(∞)=1 assicura che la decomposizione di Birkhoff, se esiste, è unica (sotto opportune condizioni di regolarità). Nel caso in cui G è un gruppo di Lie nilpotente complesso semplicemente connesso, l'esistenza e unicità della decomposizione di Birkhoff vale per un qualunque γ. Quando il cappio γ:C→G si estende a uno olomorfo C₊→G, la decomposizione di Birkhoff è data da γ₊=γ, γ₋=1. In generale, per z∈C₊ il calcolo

[80] γ→γ₊(z)∈G

è naturale per estrarre un valore finito dall'espressione singolare γ(z). Questa estrazione di valori finiti coincide con la rimozione della parte del polo quando G è il gruppo additivo ℂ dei numeri complessi e il cappio γ è meromorfo in C₊ con z unica singolarità. Il risultato principale è che la teoria rinormalizzata non è altro che il calcolo in z=D della parte olomorfa γ₊ della decomposizione di Birkhoff del cappio γ a valori in G data dalla regolarizzazione dimensionale. In effetti, la relazione che abbiamo trovato tra l'algebra di Hopf dei grafi di Feynman e l'algebra di Hopf delle coordinate sul gruppo dei diffeomorfismi formali delle costanti di accoppiamento adimensionali della teoria permette di dimostrare il seguente risultato (per semplicità consideriamo il caso di un singola costante di accoppiamento adimensionale).

Se le costanti effettive di accoppiamento non rinormalizzate g_eff(ε) sono considerate come serie di potenze formali in g, e se g_eff(ε)=g_eff+(ε)(g_eff−(ε))⁻¹ è la decompo-sizione (opposta) di Birkhoff nel gruppo dei diffeomeorfismi formali, allora il cappio g_{eff −} (ε) è la costante di accoppiamento nuda e g_eff+(0) l'accoppiamento effettivo rinormalizzato.

Ciò permette, utilizzando la relazione tra la decomposizione di Birkhoff e la classificazione di fibrati olomorfi, di codificare geometricamente l'operazione di rinormalizzazione; segnala inoltre una chiara analogia tra il gruppo di rinormalizzazione come gruppo di 'ambiguità' delle teorie fisiche e la teoria di Galois, che manca nei concetti archimedei ai quali abbiamo fatto riferimento prima.

Bibliografia

Atiyah 1969: Atiyah, Michael F., Global theory of elliptic operators, of Proceedings the international conference on functional analysis and related topics, Tokyo, Tokyo University Press, 1969, pp. 21-30.

Connes 1980: Connes, Alain, C* algèbres et géométrie différentielle, "Comptes rendus des séances de l'Académie des Sciences, Série A", 290, 1980, pp. 599-604.

Connes 1982: Connes, Alain, Noncommutative differential geometry. Part I: The Cern character in K-homology, Preprint Institut des Hautes Études Scientifiques (M/82/53), 1982 (rist. in: "Publications mathématiques. Institut des Hautes Études Scientifiques", 62, 1985).

Connes 1983: Connes, Alain, Noncommutative differential geometry. Part II: de Rham homology and noncommutative algebra, Preprint Institut des Hautes Études Scientifiques (M/83/19), 1983 (rist. in: "Publications mathématiques. Institut des Hautes Études Scientifiques", 62, 1985).

Connes 1985: Connes, Alain, Noncommutative differential geometry, "Publications mathématiques. Institut des Hautes études Scientifiques", 62, 1985, pp. 257-360.

Connes, Rieffel 1987: Connes, Alain - Rieffel, Marc A., Yang-Mills for noncommutative two tori, in: Operator algebras and mathematical physics, Proceedings of a summer conference held June 17-21, 1985 Jowa City, edited by Palle E.T. Jorgensen and Paul S. Muhly, Providence (RI), American Mathematical Society, 1987, pp. 237-279.

Connes 1994: Connes, Alain, Noncommutative geometry, San Diego, Academic Press, 1994.

Connes, Moscovici 1995: Connes, Alain - Moscovici, Henri, The local index formula in noncommutative geometry, "Geometric and functional analysis", 5, 1995, pp. 174-243.

Connes 2000: Connes, Alain, Noncommutative geometry and the Riemann zeta function, in: Mathematics: frontiers and perspectives, edited by Vladimir I. Arnold, Providence (RI), America Mathematical Society, 2000, pp. 35-54.

Connes, Kreimer 2000: Connes, Alain - Kreimer, Dirk, Renormalization in quantum field theory and the Riemann-Hilbert problem I: the Hopf algebra structure of graphs and the main theorem, "Communication in mathematical physics", 210, 2000, pp. 249-273.

Connes, Kreimer 2001: Connes, Alain - Kreimer, Dirk, Renormalization in quantum field theory and the Riemann-Hilbert problem II: the beta function, diffeomorphisms and the renormalization group, "Communication in mathematical physics", 216, 2001, pp. 215-241.

Connes, Dubois-Violette 2002: Connes, Alain - Dubois-Violette, Michel, Noncommutative finite-dimensional manifolds. I. Spherical manifolds and related examples, "Communications in mathematical physics", 230, 2002, pp. 539-579.

Connes 2002: Connes, Alain, Symétries Galoisiennes et renormalisation, Séminaire Henri Poincaré II, octobre 2002.

Skandalis 2002: Skandalis, Georges, Progrès recents sur la conjecture de Baum-Connes, Contribution de Vincent Lafforgue, "Asterisque", 276, 2002, pp. 105-135.