ipocicloide
La curva descritta da un punto P rigidamente collegato a un cerchio c (v. fig.), detto epiciclo, tangente internamente a un cerchio fisso k del suo piano e che rotoli senza strisciare su k.
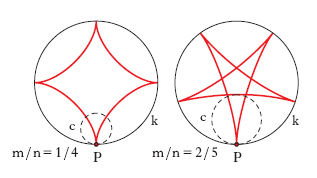
L’i. è ordinaria, accorciata o allungata a seconda che il punto P sia, rispettivamente, sul cerchio mobile, al suo interno o al suo esterno; limitatamente al primo caso si hanno le seguenti proprietà. Se il raggio r di c è la metà del raggio R di k, l’i. si riduce a un diametro di k: è questo il teorema di Cardano. In generale, se il rapporto tra i raggi dei due cerchi è espresso dal numero razionale irriducibile m/n, l’i. ha l’aspetto di una stella a n punte, ed è una curva algebrica. Inoltre, la curva non è intrecciata se m=1. Nella fig. sono illustrate le curve che si ottengono per i valori 1/4 e 2/5 del rapporto m/n. La curva che si ha per m/n=1/4 è detta asteroide. L’i. è invece una curva trascendente se il rapporto m/n è irrazionale, ossia se i raggi dei due cerchi sono incommensurabili.