lunula
Anatomia
Piccola zona di colorito biancastro, limitata da una linea curva regolare, che si osserva alla base dell’unghia. È dovuta all’accumulo, sotto la lamina ungueale, delle cellule dello strato onicogeno.
Si chiama l. anche ognuno dei due segmenti in cui il margine libero di ogni valvola semilunare del cuore è diviso dal proprio nodulo.
Matematica
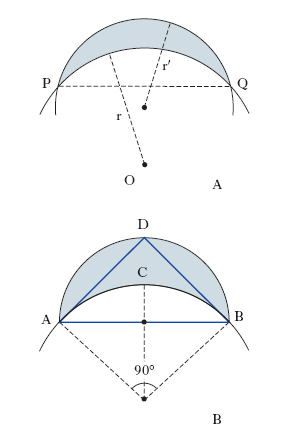
In geometria, regione piana limitata da due archi circolari di raggio diverso (r, r′) aventi gli estremi P, Q in comune e giacenti da una stessa parte rispetto alla corda che li sottende (fig. A). Ippocrate di Chio (5° sec. a.C.) riconobbe quadrabili tre tipi di l. (l. di Ippocrate). Tra le l. di Ippocrate, la più semplice si ottiene considerando un arco ACB che sia la quarta parte di una circonferenza (fig. B) e costruendo poi la semicirconferenza ADB che ha per diametro la corda AB di detto arco e che giace dalla stessa parte di esso rispetto ad ACB. La superficie di tale l. è uguale a quella del triangolo rettangolo isoscele di ipotenusa AB. Altri due tipi di l. quadrabili furono trovati da J. Clausen (1840). Non si sa se questi 5 tipi esauriscano o no la classe delle l. quadrabili elementarmente. Tuttavia nel 1903 E. Landau ha dimostrato che i tipi di l. quadrabili con mezzi elementari non sono infiniti.