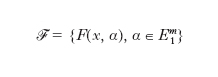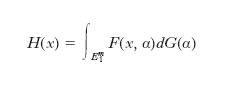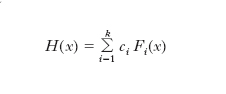mistura di distribuzioni
In statistica, procedimento per ottenere una funzione di distribuzione che sia una media pesata di un dato gruppo di funzioni di distribuzione. Il caso di distribuzioni risultanti dalla m. di altre distribuzioni si presenta frequentemente. Tali situazioni sorgono, per es., in biologia, in antropometria, nella correzione di rilevazioni statistiche, quando il fenomeno allo studio è il risultato dell’unione di varie componenti che seguono distribuzioni più o meno differenziate. Matematicamente il problema può essere rappresentato come segue: sia data una famiglia
di funzioni di ripartizione unidimensionali, dipendenti da un punto variabile in un sottoinsieme boreliano E1m dello spazio euclideo Em. La funzione di ripartizione unidimensionale:
,
dove G è una funzione di ripartizione m-dimensionale, è una mistura. La classe delle m. è detta identificabile se vi è una corrispondenza univoca tra le funzioni G e le funzioni H. Solo limitatamente al caso m=1 e per particolari famiglie ℱ si conoscono le condizioni necessarie e sufficienti d’identificabilità. Più semplice è il caso finito, in cui le m. sono espresse mediante una combinazione lineare:
con coefficienti ci positivi e di somma uno. È stato dimostrato, per es., che la classe delle m. finite delle distribuzioni normali e la classe delle distribuzioni gamma sono identificabili. Per le m. finite identificabili si pone il problema della stima campionaria dei coefficienti ci, che può essere affrontato mediante il metodo dei momenti oppure mediante quello dei minimi quadrati.