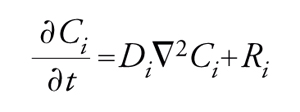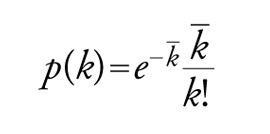Sistemi reagenti complessi

Sistemi reagenti complessi

La chimica ha raggiunto un soddisfacente grado di sviluppo, in virtù del quale costituisce un efficace e indispensabile strumento per la comprensione dei fenomeni naturali, inclusi quelli che riguardano le scienze della vita. Inoltre, essa occupa un ruolo di primo piano nella progettazione e nello sviluppo di tecnologie avanzate, mediante le quali si preparano carburanti, polimeri, materiali, farmaci, e così via. Infine, essa offre la possibilità di affrontare problemi di frontiera, talora con un profondo contenuto culturale. Per esempio, le ricerche sull'origine della vita non possono prescindere da un'adeguata e profonda conoscenza dei meccanismi attraverso i quali i sistemi macromolecolari si autoorganizzano per acquisire ben definite funzionalità.

Le scienze chimiche stanno sempre più evolvendo verso la descrizione dei sistemi complessi di molecole, in stretta connessione con altre discipline quali la fisica, la scienza dei materiali e la biologia. I problemi che vengono affrontati sono diversificati, poiché riguardano, per esempio, le complesse sequenze di reazioni che intervengono nei processi biologici, la distribuzione nell'atmosfera dei gas serra, i processi di autoorganizzazione molecolare. Inoltre, dal comportamento dinamico dei sistemi chimici complessi possono emergere strutture ordinate e coerenti nel tempo e nello spazio, in apparente contrasto con quanto previsto dal secondo principio della termodinamica, che privilegia l'implacabile decadimento verso il disordine.

Le acquisizioni conseguite nel settore delle scienze molecolari hanno conferito alla chimica contemporanea la capacità di affrontare, con confidenza e affidabilità, problematiche che coinvolgono conoscenze dettagliate sulle strutture e sulle trasformazioni cui la materia è soggetta, attraverso una successione gerarchica di eventi che procedono dal livello microscopico a quello macroscopico, in un vertiginoso passaggio di scala di dieci ordini di grandezza: ovvero dalle dimensioni atomiche a quelle ordinarie.

Questo approccio fornisce i criteri per la descrizione e la modellazione di fenomeni di interesse vario e fornisce un prezioso orientamento nell'esplorazione di particolari comportamenti che hanno importanti ricadute nei settori riguardanti le sintesi condotte a elevate temperature, la combustione, la preparazione di materiali avanzati, la chimica atmosferica, la chimica dei processi biologici.

Le ricerche che vengono condotte fruiscono da un lato dello sviluppo di metodologie analitiche sempre più sofisticate, che permettono di individuare la presenza di piccole quantità di reagenti di diversa natura, spesso caratterizzati da una vita media molto breve, da un altro lato traggono giovamento dalle recenti acquisizioni nel settore della chimica computazionale, grazie alla quale è attualmente possibile simulare con ragionevole accuratezza gli eventi microscopici delle reazioni in gioco.

Sistemi complessi di reazioni

A differenza di quanto possa apparire a un primo esame, gran parte delle trasformazioni chimiche si svolgono attraverso un insieme molto elevato di trasformazioni semplici, dette elementari, che si sovrappongono e si incrociano dando origine a una complessa rete di interconnessioni. Per esempio, se si fa interagire l'ossigeno con il metano (che è l'idrocarburo più semplice, con formula CH₄), ha luogo una trasformazione che in particolari condizioni diviene rapidissima, al limite esplosiva, e che globalmente porta alla formazione di acqua (H₂O) e anidride carbonica (CO₂). Questo processo, che sta alla base della produzione di energia, anche se apparentemente semplice coinvolge in realtà decine di composti chimici che interagiscono attraverso uno schema comprendente un elevato numero di reazioni elementari.

L'energia necessaria per alimentare le trasformazioni che avvengono negli organismi viventi viene a sua volta prodotta da un processo di combustione di polimeri naturali chiamati idrati di carbonio (o carboidrati) e ottenuti nella fotosintesi clorofilliana, il più comune dei quali è l'amido. I carboidrati, infatti, vengono trasformati in anidride carbonica e acqua. Anche in questo caso interviene un ciclo complesso di reazioni − detto ciclo di Krebs − del tutto diverso dal precedente, poiché avviene in una soluzione acquosa, a temperatura ordinaria e con una velocità globale compatibile con quella degli altri processi che hanno luogo negli organismi viventi stessi. E ciò grazie all'azione catalitica degli enzimi, che sono chimicamente costituiti da proteine.

L'analisi e la simulazione dei processi menzionati può essere perseguita attraverso la determinazione dei parametri cinetici che condizionano la velocità delle trasformazioni elementari in essi coinvolti. Per perseguire l'obiettivo è necessario evidenziare le caratteristiche strutturali e dinamiche di configurazioni instabili derivanti dalla collisione di molecole diverse, dette complessi attivati, che giocano un ruolo determinante sulla velocità delle reazioni elementari. Recentemente Ahmed Zewail, premio Nobel per la chimica nel 1999, attraverso l'impiego della spettroscopia basata su impulsi laser molto brevi dell'ordine dei femtosecondi (10⁻¹⁵ s) è riuscito a determinare sperimentalmente le caratteristiche geometriche di alcuni di tali complessi attivati. Infatti, colpendo particolari molecole con impulsi di due diversi laser è possibile fotografare il momento preciso in cui si rompono i legami fra alcuni atomi e se ne formano di nuovi.

schema

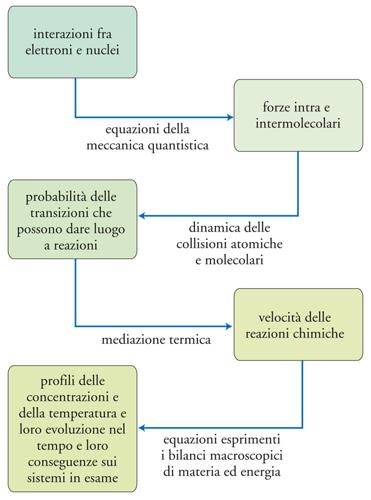
Dal punto di vista strettamente teorico, lo studio della dinamica dei sistemi reagenti può essere perseguito attraverso una successione gerarchica di eventi che procede dalle variabili microscopiche a quelle macroscopiche seguendo lo schema.

Questa impostazione contempla una transizione dalle dimensioni atomiche, corrispondenti a 10⁻⁸ cm, a quelle ordinarie che ammontano a decine di cm. Lo schema precedente, naturalmente, vale sia per processi che avvengono in una miscela gassosa, sia per reazioni che hanno luogo nei sistemi condensati, in particolare nelle soluzioni liquide. In quest'ultimo caso, ovviamente, il processo di mediazione termica coinvolge anche le molecole del solvente che si trovano a stretto contatto con i reagenti.

Approccio sintetico allo studiodei sistemi reagenti complessi

La menzionata complessità di gran parte dei sistemi reagenti presenti in natura, spesso pone severe limitazioni a una loro analisi, nella quale si voglia tenere conto di tutti i fenomeni elementari in essi coinvolti. In realtà, per alcuni aspetti questo approccio appare ingiustificato, poiché solo raramente si dispone di informazioni sufficienti per perseguirne una descrizione così dettagliata.

Fortunatamente, spesso solo alcune delle reazioni condizionano l'evoluzione del sistema e la velocità del processo globale. Poiché ciascuna di esse ha una particolare velocità che dipende dalle condizioni operative, finiscono per prevalere quei cammini di reazione che risultano più agevoli dal punto di vista cinetico. Pertanto, si apre il problema di individuarli in modo da poter semplificare gli schemi cinetici, pur mantenendo però le caratteristiche peculiari del sistema in esame. In questa impostazione, l'evoluzione viene descritta attraverso alcune reazioni significative, utilizzando valori efficaci dei parametri cinetici che ne caratterizzano il comportamento in corrispondenza di una particolare scala temporale, spaziale o termica. Per esempio, la menzionata reazione di combustione del metano, che si svolge coinvolgendo un numero molto elevato di composti intermedi presenti in piccola concentrazione, in prima approssimazione può essere descritta mediante una reazione globale che trasforma il metano in anidride carbonica e acqua, trascurando la presenza delle altre specie.

Questo tipo di approccio è utile se siamo interessati a valutare la quantità di energia che si libera nel processo di combustione. È però inadeguato se si vuole valutare la formazione di composti inquinanti, quali gli ossidi di azoto (NO_x), favorita dalla presenza di intermedi che, pur essendo presenti in quantità apparentemente trascurabili, finiscono per giocare un ruolo importante quando si ponga l'attenzione ai problemi connessi con il controllo dell'ambiente. Questi fatti giustificano l'intensificarsi di ricerche nelle quali, attraverso l'impiego di metodologie diagnostiche molto sofisticate, si possono individuare specie presenti in concentrazioni molto piccole.

Nella trattazione che segue, ci riferiremo a sistemi reagenti aperti, identificando una zona dello spazio in corrispondenza della quale siano presenti flussi di materia entranti e uscenti, che contengono rispettivamente i reagenti e i prodotti di reazione. In condizioni stazionarie, la somma dei flussi entranti eguaglia quella dei flussi uscenti e i valori delle diverse concentrazioni si mantengono inalterati nel tempo. In generale, però, il sistema è soggetto a trasformazioni in virtù delle quali ha luogo un accumulo o un depauperamento di alcuni dei composti. Rientrano in questa tipologia molti sistemi naturali e industriali, che comprendono, fra gli altri: (a) l'atmosfera, che costituisce una vera e propria 'zuppa chimica', grazie alla presenza in quantità molto piccole di componenti che ‒ interagendo fra loro ‒ possono portare a evoluzioni indesiderate; (b) le cellule biologiche, nelle quali si intrecciano le diverse reazioni enzimatiche che stanno alla base del loro metabolismo, del loro controllo e del loro sviluppo; (c) il cosiddetto brodo prebiotico, nel quale attraverso l'interazione di diversi componenti chimici si sono manifestate interessanti proprietà emergenti, che hanno favorito la formazione di strutture molecolari ordinate; (d) le unità industriali, nelle quali si realizzano le sintesi chimiche; (e) le unità di produzione di energia attraverso processi di combustione.

Talora questi sistemi reagenti manifestano l'insorgenza di configurazioni ordinate nel tempo e nello spazio, oppure configurazioni irregolari e caotiche. L'esempio più noto è costituito dalla reazione di Belousov-Zhabotinsky, nella quale ha luogo l'ossidazione di un acido organico (per es., acido maleico) in presenza di bromati alcalini e sali di cerio in una soluzione acida. In questa reazione, infatti, si manifesta una oscillazione nel tempo della concentrazione dello ione cerio, nei suoi diversi stati di ossidazione, accompagnata da effetti cromatici tipici. Anche se il meccanismo specifico della reazione non è ancora ben noto, sono sicuramente presenti effetti dovuti a retroazioni, in virtù delle quali uno dei prodotti di reazione influenza la velocità di una delle reazioni che ha preceduto la sua formazione. La simultanea presenza di queste reazioni autocatalitiche e della diffusione dei reagenti può dare origine a un ordine spazio-temporale.

Dal punto di vista matematico, questi sistemi vengono descritti mediante equazioni differenziali di secondo ordine alle derivate parziali non lineari, che riflettono i bilanci di materia dei diversi componenti, condotti su un elemento di volume, tenendo conto degli effetti dovuti alle reazioni chimiche e alla diffusione. Per un generico componente i, la cui concentrazione è C_i, l'equazione di bilancio assume la forma seguente:

[1] formula

dove t è il tempo, D_i il coefficiente di diffusione e ∇²C_i∝C−_i−C_i(P) è il laplaciano, che, a meno di un fattore numerico, fornisce una misura della differenza fra il valore medio della concentrazione C−_i del componente i, valutato dai valori nell'immediato intorno di un punto P, e il valore nel punto P stesso. R_i è la velocità di reazione che esprime la quantità del componente in esame che viene trasformata per unità di tempo e di volume. Essa dipende dalle concentrazioni dei diversi componenti e dalla temperatura. Il termine al primo membro dell'equazione precedente esprime l'accumulo del componente, mentre i due termini al secondo membro esprimono, rispettivamente, i contributi della diffusione e della reazione chimica.

La non linearità, presente nell'espressione della velocità di reazione, costituisce un requisito indispensabile perché si possano manifestare gli effetti menzionati e consegue dal fatto che, dal punto di vista microfisico, una reazione chimica trae origine dall'incontro di due molecole. La probabilità dell'evento, allora, risulta proporzionale al prodotto delle concentrazioni delle sostanze reagenti per cui la sua velocità risulterà a sua volta espressa da una relazione matematica di tipo quadratico. Un'ulteriore fonte di non linearità è dovuta al fatto che l'influenza della temperatura sulla velocità di reazione si esprime con la relazione esponenziale che, rappresentata graficamente, presenta un tipico andamento a S.

Sino a qualche anno fa, la non linearità ha costituito un problema di difficile soluzione per chi era impegnato nello studio dell'evoluzione nel tempo di sistemi soggetti a reazioni chimiche. Essa, infatti, impediva di ottenere la soluzione analitica delle equazioni di bilancio. Lo sviluppo dei calcolatori ha cambiato la situazione, poiché ha reso possibile la soluzione per via numerica delle impenetrabili equazioni differenziali della dinamica chimica.

fig. 2

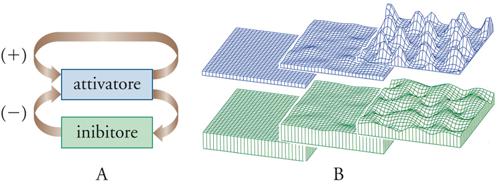
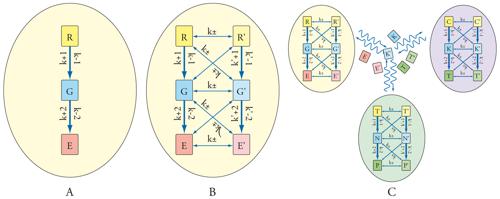
L'emergenza di andamenti oscillanti nel tempo e nello spazio delle concentrazioni delle diverse specie in gioco era stata anticipata da Alan Turing nel 1952, in un lavoro pionieristico nel quale si evidenziava che lo sviluppo di strutture spaziali consegue da perturbazioni cui è soggetto il sistema reagente stesso, dovute a fluttuazioni di concentrazione o di temperatura, in conseguenza delle quali − in un mezzo uniforme e quindi simmetrico − si generano configurazioni spazio-temporali meno simmetriche ma più ordinate. L'intento di Turing era di giustificare i cosiddetti processi morfogenici che si manifestano nei sistemi biologici, attribuendoli all'effetto esercitato da opportune sostanze chimiche (chiamate morfogeni) sulla velocità delle reazioni biochimiche presenti nel sistema. Un esempio interessante, e profondamente studiato, è quello in cui è presente un meccanismo autocatalitico con retroazione nel quale uno dei componenti di una serie di reazioni successive influisce su una delle reazioni che precede la sua formazione, aumentandone o diminuendone la velocità. Questi effetti di attivazione e di inibizione interagiscono reciprocamente, e possono essere modulati dalla differenza fra la velocità di diffusione dei componenti stessi (fig. 2). In questo modo si formano distribuzioni delle concentrazioni che risultano non uniformi nello spazio. I risultati ottenuti hanno acquistato interesse anche per i sistemi viventi, soprattutto in seguito alla scoperta di alcuni fattori biosintetici autoesaltanti quali, per esempio, alcune proteine regolatrici di geni che potrebbero indurre aggregazioni cellulari che, a loro volta, precedono le differenziazioni che stanno alla base della formazione di strutture scheletrali articolate presenti negli organismi viventi.

In realtà, la possibilità di applicare l'elegante lavoro matematico di Turing ai processi morfogenici biologici è stata però oggetto di controversie. E ciò, soprattutto, in seguito alla scoperta che le sette strisce presenti nell'embrione della drosofila (la mosca della frutta), che sembravano una sua ideale applicazione, sorgono indipendentemente una dall'altra, per azione di gradienti di concentrazione che influenzano la struttura delle proteine attraverso una successione a cascata. Un'obiezione che viene avanzata al modello diffusione-reazione da alcuni scienziati, in particolare Sean B. Carroll, risiede nel fatto che esso ignora l'esistenza di interruttori genetici modulari, in virtù dei quali le figure osservate risultano composte da una molteplicità di elementi.

Il lavoro di Turing e dei suoi epigoni ha però riacquistato un interessante rilancio in seguito a un recente lavoro sperimentale di Stefanie Sick e altri, nel quale si dimostra che la formazione di particolari pattern nel-la distribuzione dei follicoli contenenti peli, può essere modellato mediante un processo di reazione-diffusione manipolando opportunamente una coppia di geni dei topi.

In realtà, l'interpretazione su basi chimico-fisiche dei processi morfogenetici biologici comprende ‒ oltre a quella illustrata, del tipo reazione-diffusione ‒ una classe ampia di comportamenti nei quali si fanno intervenire altri fattori fisici, quali la separazione fra fasi liquide diverse, la tensione superficiale, gli effetti gravitazionali e la viscosità. Essi si contrappongono agli effetti dominati da fattori genetici che stanno alla base dei processi di sviluppo, condizionati da interazioni altamente organizzate tra macromolecole specifiche.

Reti di reazioni biologiche e sistemi cellulari

Nella biologia molecolare sono ancora sporadici i modelli quantitativi simili − per generalità, compattezza ed eleganza − a quelli familiari ai fisici. Infatti, essi non si sono ancora riscattati da un carattere empirico, strettamente ancorato alle informazioni ottenute dalle misure sperimentali. Tuttavia, da alcuni anni sta maturando la consapevolezza che esista una concreta possibilità di formulare modelli cellulari che, pur fruendo dei risultati delle esperienze, contribuiscano non solo ad aumentare le nostre conoscenze sul comportamento dei sistemi cellula-ri, ma anche a prevederlo, quando essi sono sottoposti a sollecitazioni esterne. Le ragioni di questo ottimismo risiedono nell'aumento delle informazioni che si stanno acquisendo sui meccanismi enzimatici alla base dei processi biologici, ma anche nella disponibilità di calcolatori sempre più potenti. Questi, infatti, offrono la possibilità di risolvere con accuratezza i complessi sistemi di equazioni differenziali che esprimono i bilanci materiali dei diversi componenti.

fig. 3

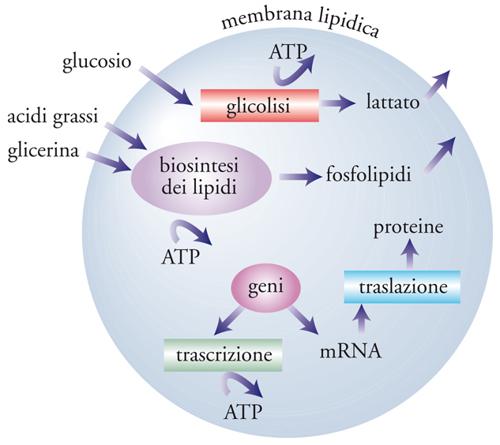
Questo approccio è inteso a costruire modelli cellulari virtuali, o in silico, come si suole dire, che fruendo delle conoscenze sperimentali su come le molecole diffondono e reagiscono entro le cellule stesse, ne evidenzino il comportamento. Un esempio viene riportato nella fig. 3, dove sono schematizzati i principali processi biochimici che hanno luogo in una cellula. Essi, in particolare, riguardano tre aspetti fondamentali del metabolismo cellulare: (a) quello energetico, attraverso i processi in cui ha luogo la demolizione del glucosio con formazione dell'adenosin-trifosfato (ATP), che si comporta come il vettore energetico o il 'carburante' degli altri processi; (b) quello strutturale, attraverso la sintesi dei lipidi che, autoassemblandosi, formano la membrana cellulare; (c) quello del controllo e dello sviluppo attraverso la sintesi delle proteine, gestite dai geni, presenti nel nucleo, quali depositari del patrimonio di informazioni contenute nella cellula. Le proteine, a loro volta, svolgono molte attività funzionali che caratterizzano il livello organizzativo della cellula stessa.

fig. 4

Nei processi metabolici che si svolgono attraverso una serie di reazioni sequenziali e accoppiate (fig. 4), ha luogo la trasformazione di materie prime attinte dall'ambiente nelle molecole richieste alle cellule, producendo nel contempo energia. Si tratta di vere e proprie architetture costruite su nodi formati da particolari molecole, geni o proteine, che interagiscono reciprocamente, sia pure con la presenza di cammini preferenziali (signaling).

Queste interazioni molecolari, geneticamente programmate, condizionano il controllo e lo sviluppo delle cellule stesse. Inoltre, si possono manifestare proprietà emergenti caratterizzate dalla comparsa di comportamenti non prevedibili dalle proprietà dei singoli componenti presenti nel sistema. Tipica è l'insorgenza di cicli di retroazione che possono comportarsi come interruttori per il controllo del flusso di informazione.

fig. 5

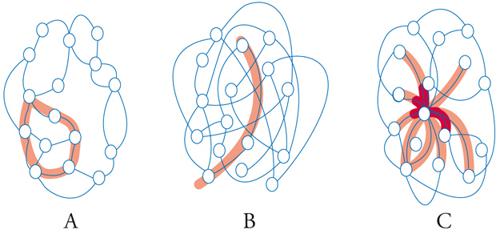
Per individuare una strategia di indagine è opportuno riferirsi alla teoria statistica delle reti (network) rappresentando tali cicli come un insieme di sottounità (o nodi) che interagiscono o comunicano fra di loro. Tutto ciò senza richiedere la presenza di una speciale struttura metrica che attribuisca ai nodi una ben definita posizione nello spazio. Ciascun nodo è connesso mediante k legami agli altri e la maniera con la quale vengono attuati i legami condiziona il comportamento della rete. Infatti (fig. 5) esse possono essere: (a) regolari, se sono presenti gruppi locali di nodi interconnessi; (b) casuali, se sono assenti gruppi di nodi ma la rete è facilmente attraversabile; (c) a scala libera (scale free), se la rete è facilmente attraversabile pur esistendo gruppi di nodi interconnessi.

Se si assume che, durante l'evoluzione della rete, tutti i nodi siano equivalenti e accessibili, e che si uniscono ad altri con uguale probabilità, mantenendo il loro numero inalterato durante la vita della rete stessa, la probabilità che un nodo scelto a caso abbia un numero k di interconnessioni risulta espressa da:

[2] formula

dove k− è il numero medio di legami, detto anche scala della rete. La precedente costituisce una tipica distribuzione di Poisson rispetto al numero medio di nodi, ed è caratteristica delle cosiddette reti di Erdos-Renyi.

Molto spesso, però, non è possibile attribuire alla rete una scala specifica per cui la probabilità risulta espressa da una legge di potenza del tipo:

[3] p(k)∝k^γ con γ=1÷3.

La validità di questa relazione è stata riscontrata, anche empiricamente, nella descrizione di sistemi non solo di interesse chimico-biologico, ma anche ecologico, economico e sociale. Può essere giustificata in diversi modi, in particolare assumendo che l'evoluzione della rete proceda con l'aggiunta, a intervalli regolari di tempo, di un nuovo nodo e che ciascun nodo si connetta con gli altri con una probabilità proporzionale al numero di nodi che già possiede. La descrizione dell'evoluzione della rete, effettuata mediante una serie di equazioni simili a quelle impiegate per studiare quella dei prodotti di una serie di reazioni successive, giustifica un comportamento compatibile con una relazione a scala libera.

L'analisi sperimentale di decine di reti metaboliche, riferite a diversi organismi che vanno dai batteri alle piante, ha confermato che la connettività della loro distribuzione è del tipo a scala libera. Per approfondire questo importante risultato, si può osservare che le migliaia di reazioni enzimatiche, che danno luogo ai flussi metabolici, possono essere esplorate con i metodi della cinetica chimica, traendo vantaggio del fatto che esse esercitano un controllo dei flussi energetici e della produzione dei componenti cellulari che entrano nel metabolismo. La formulazione di uno schema delle diverse reazioni che intervengono nel processo risulta purtroppo impossibile, poiché se ne possono formulare diversi in grado di descrivere la formazione dei dif-ferenti composti in gioco. Per fare una scelta si assume che, in condizioni stazionarie dei flussi metabolici, sia massima la velocità di produzione della biomassa che contribuisce alla crescita del sistema ed espressa attraverso una combinazione lineare dei flussi metabolici stessi (flux balance analysis).

L'analisi dei dati sperimentali rivela allora una mancanza di omogeneità nella distribuzione dei flussi poiché alcuni di essi prevalgono nettamente sugli altri e, al limite, può risultare che in una singola reazione domini la trasformazione di alcuni metaboliti. Questo risultato è compatibile con il fatto che la rete che descrive l'insieme delle reazioni metaboliche è invariante rispetto alla scala. Non solo, ma la mancanza di omogeneità fra i flussi riflette anche la presenza di una struttura del sistema, poiché i collegamenti fra le diverse reazioni soddisfano particolari topologie.

Tale interessante risultato ci induce a ritenere che esso costituisca un riflesso della storia evolutiva del metabolismo. Questa potenziale relazione fra la storia evolutiva e la connettività delle reti metaboliche corrobora un postulato avanzato da Harold Morowitz in base al quale si assume che il metabolismo intermedio ricapitoli l'evoluzione biochimica del sistema metabolico nel suo complesso.

fig. 6

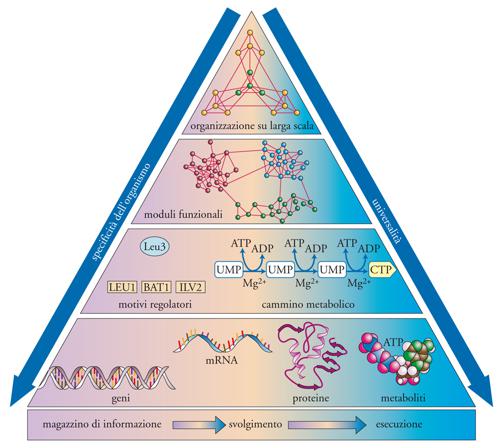
Più in generale, se le cellule e i microrganismi sono visti come una rete di geni e proteine, si può individuare una strategia per affrontare la complessità degli organismi viventi, sintetizzata con la piramide illustrata nella fig. 6, dove i moduli presenti nella parte inferiore si organizzano in una struttura gerarchica che definisce l'organizzazione funzionale delle cellule sulle scale crescenti.

I problemi della dinamica evolutiva di un sistema di cellule vengono affrontati anche con modelli più semplici, che comprendono però, quali aspetti essenziali, sia i processi di crescita che quelli di divisione. Per esempio, ipotizzando che in ciascuna cellula, protetta dall'ambiente da una membrana permeabile, abbia luogo un insieme di reazioni collettivamente autocatalitiche, che coinvolgono composti con il comportamento chimico tipico delle sostanze che intervengono nei processi metabolici. Le interazioni fra le diverse cellule avvengono attraverso l'ambiente circostante. In sostanza, ciascuna cellula viene assimilata a un sistema, reagente, aperto ai flussi di materia con l'esterno in modo da poter ricevere le sostanze nutrienti ed eliminare alcuni prodotti delle reazioni. Quando le quantità di uno o più costituenti superano una determinata soglia la cellula si divide. Viceversa alcune cellule possono morire per difetto di nutrimento. In questa impostazione, la differenziazione e l'evoluzione cellulare emergono dalla dinamica dei processi precedentemente descritti. Le equazioni che esprimono ilbilancio materiale dei diversi componenti contengono − oltre ai termini che esprimono − l'influenza della velocità delle reazioni in gioco sulla loro variazione, e anche quelli associati al loro trasporto verso l'esterno attraverso la membrana. Il modello così descritto, anche se semplificato, rivela una dinamica evolutiva in grado di simulare il comportamento di culture cellulari reali e che può essere mutuato per descrivere il comportamento di sistemi formati da unità in grado di replicarsi, quali la società umana e i sistemi ecologici.

Conclusioni

I sistemi chimici complessi manifestano una vasta tipologia di comportamento, che spesso presenta proprietà peculiari. La loro analisi costituisce una ricca fonte di modelli estremamente efficaci per esplorare nuovi territori nei quali la chimica gioca un ruolo di primo piano. Essi riguardano sia i sistemi naturali che quelli relativi ai processi produttivi, nei quali sono presenti reti di reazioni interconnesse la cui dinamica fa emergere situazioni talora imprevedibili. Tutto ciò con la piena consapevolezza che l'approccio riduzionistico della biologia molecolare, pur essendosi rivelato estremamente potente, non tiene adeguatamente conto dei processi di interazione che hanno luogo a diversi livelli, che vanno da quello molecolare all'intero organismo. Alcuni esempi significativi, illustrati nella trattazione precedente, si riferiscono ai processi morfogenetici che si manifestano nelle strutture organiche. Ma ancora più ambiziose e affascinanti sono le ricerche intese a simulare il comportamento dei sistemi viventi. Alla loro base si devono fronteggiare due problemi fondamentali: (a) in che modo una collezione di molecole può dare origine alla varietà di comportamenti che caratterizzano le cellule; (b) in che modo le molecole possono assemblarsi in un insieme che abbia la capacità di dissipare l'energia, di autoreplicarsi e di adattarsi all'ambiente.

Allo stato attuale non è possibile stabilire se le conoscenze sulle caratteristiche delle molecole e delle loro interazioni ci potranno offrire una risposta ai quesiti precedenti. Si tratta, comunque, di un programma che merita di essere perseguito.

Però è importante osservare che, se si sanno cogliere aspetti peculiari dei sistemi presi in considerazione, risulta possibile formulare alcuni interessanti modelli che offrono la possibilità di evidenziare l'emergenza di comportamenti inaspettati e di particolare interesse. Fra questi aspetti, sono state considerate la non linearità delle leggi cinetiche, la competizione fra le reazioni chimiche e la diffusione e i processi di retroazione, dimostrando come essi costituiscano strumenti efficaci per l'esplorazione di sistemi complessi soggetti a trasformazioni chimiche.

Bibliografia

Carrà 1989: Carrà, Sergio, La formazione delle strutture, Torino, Bollati Boringhieri, 1989.

Carrà 1998: Carrà, Sergio, Autorganizzazione, in: Enciclopedia del Novecento, Supplemento II, Roma, Istituto della Enciclopedia Italiana, 1998, pp. 75-99.

Carrà, Morbidelli 1983: Carrà, Sergio - Morbidelli, Massimo, Chimica-fisica applicata, Milano, Hoepli, 1983.

Carroll 2005: Carroll, Sean B., Endless forms most beautiful, New York, Norton, 2005.

Eigen 1971: Eigen, Manfred, Cell organization of matter and evolution of biological macromolecules, "Naturwissenschaften", 58, 1971, pp. 465-523.

Endy, Brent 2001: Endy, Drew - Brent, Roger, Modelling cellular behaviour, "Nature", 409, 2001, pp. 391-395.

Kunihiko, Tetsuya 1999: Kunihiko, Kaneko -Tetsuya, Yomo, Isologous diversification for robust development of cell society, "Journal of theoretical biology", 199, 1999, pp. 243-256.

Mazzotti, Carrà 1995: Mazzotti, Marco - Carrà, Sergio, Phase transition and symmetry in reacting chemical systems, in: Ana-lysis, simulation, dynamics of chemical reactors, a cura di Gaetano Continillo, Silvestro Crescitelli e Pier Giorgio Lignola, Napoli, CUEN, 1995, pp. 225-290.

Meinhardt 1992: Meinhardt, Hans, Pattern formation in biology: a comparison of models and experiments, "Reports on progress in physics", 55, 1992, pp. 797-849.

Newman, Comper 1990: Newman, Stephen A. - Comper, Wayne D., Generic physical mechanisms of morphogenesis and pattern formation, "Development", 110, 1990, pp. 1-18.

Normile 1999: Normile, Dennis, Building working cells "in silico", "Science", 284, 1999, pp. 80-81.

Peacocke 1983: Peacocke, Arthur R., An introduction to the physical chemistry of biological organizations, Oxford, Clarendon, 1983.

Réka, Barabasi 2002: Réka, Albert - Barabasi, Albert-László, Statistical mechanics of complex networks, "Reviews of modern physics", 74, 2002, pp. 47-97.

Service 1999: Service, Robert F., Exploring the systems of life, "Science", 284, 1999, pp. 80-83.

Sick 2006: Sick, Stefanie e altri, WNT and DKK determine hair follicle spacing through a reaction-diffusion mechanism, "Sci-ence", 314, 2006, pp. 1447-1450.

Solé, Goodwin 2000: Solé, Richard P. - Goodwin, Brian, Signs of life, New York, Basic Books, 2000.

Tomita 2001: Tomita, Masaru, Whole-cell simulation: A grand challenge of the 21^st century, "Trends in biotechnology", 19, 2001, pp. 205-210.

Turing 1952: Turing, Alan M., The chemical basis of morphogenesis, "Philosophical transactions of the Royal Society (Series B)", 237, 1952, pp. 37-72.

Whitesides 1999: Whitesides, George M., Complexity in chemistry, "Science", 284, 1999, pp. 89-92.