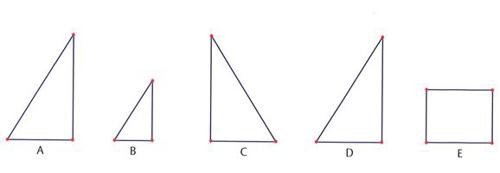geometria

geometria

Dalla misura della Terra all'organizzazione degli spazi

La geometria, 'sorella' dell'aritmetica e dell'algebra, è una parte della matematica che oggi si studia a scuola, ma è nata come scienza pratica per misurare i terreni e si è sviluppata come teoria rigorosa in cui tutto deve essere dimostrato; da sempre accompagna l'architettura e la pittura; riguarda le figure, ciò che vediamo, lo spazio in cui viviamo. Ma quante cose è la geometria?

Geometria nella natura, nel mondo

La geometria si occupa di ciò che è sotto gli occhi di tutti: figure, costruzioni, regolarità. Il nostro occhio coglie una regolarità quando giudica se una persona è alta o bassa, grassa o magra, oppure quando si accorge che il viso e il corpo di ogni essere vivente presentano qualche simmetria: il naso e la bocca al centro; gli occhi, le braccia, le gambe uguali e simmetriche. Uguali e basta, si potrebbe dire: ma non è così, come sa chiunque abbia provato a calzare la scarpa destra con il piede sinistro.

Nel guardarsi allo specchio un essere umano si riconosce, ma l'immagine riflessa non è esattamente uguale a lui: alzando il braccio destro, nello specchio si alza il sinistro: tutto è simmetrico. Guardando una fotografia, anche scattata anni prima, un essere umano riconosce sé stesso: spesso molti particolari sono cambiati, ma ciò che è rimasto invariato gli permette comunque di riconoscersi.

La proprietà geometrica della simmetria è presente in molti elementi della natura: nei fiori, negli animali, nei cristalli. È presente anche in molti oggetti costruiti dagli esseri umani, come templi, palazzi, decorazioni. Ma c'è molta altra geometria nel nostro mondo. Le case in cui viviamo sono fatte di linee e superfici piane ed è quasi impossibile contare quanti angoli retti ci sono in una stanza.

C'è molta geometria, perciò, sia nella natura sia nell'ambiente che l'uomo ha costruito; ci sono regolarità che si intravedono, come le simmetrie; regolarità volute e costruite, come gli angoli retti.

Tuttavia la geometria è una parte della matematica: non appartiene al mondo; nasce e si sviluppa nel momento in cui l'uomo, pensando e ragionando, ha dovuto risolvere qualche problema riguardante linee e superfici.

Le origini della geometria in Egitto

Secondo lo storico greco Erodoto (5° secolo a.C.) l'origine della geometria (parola composta da due termini greci, il cui significato è "misurazione della Terra") si deve far risalire agli antichi Egizi. In Egitto chi possedeva un terreno era tenuto a pagare una tassa; ma ogni anno il Nilo straripava tra luglio e ottobre e invadeva con le sue acque territori molto estesi, modificandone la conformazione e l'estensione. Il faraone inviava allora tecnici per misurare nuovamente le superfici in modo che ognuno pagasse il giusto tributo.

La geometria nasce indubbiamente come una scienza pratica e gli Egizi hanno certamente contribuito alla sua nascita: sapevano come costruire angoli retti e quindi avevano una conoscenza empirica del teorema di Pitagora. Tuttavia nozioni pratiche di geometria erano certamente presenti anche tra le popolazioni della Mesopotamia: i Sumeri e gli Assiri. Erano conoscenze non sistematiche, utili per viaggiare, per mare o per terra, e per regolare i cicli dell'agricoltura. Per prevedere le piene del Nilo e preparare la semina serviva un buon calendario e quindi bisognava studiare il moto del Sole. Per orientarsi nei viaggi per via di terra e di mare occorreva osservare le stelle, il loro movimento e le figure che descrivono in cielo, le costellazioni. Di conseguenza si dovettero via via formare caste specializzate di scribi, sacerdoti, astrologi, figure diverse che studiavano il modo di raccordare ai cicli della natura e alle regolarità visibili nel tempo e nello spazio le forme sempre più complesse di organizzazione produttiva e sociale.

Nell'antica Grecia la geometria diventa scienza

I problemi geometrici e scientifici ‒ anche di grande importanza ‒ che si sapevano risolvere nelle civiltà mesopotamiche e nell'antico Egitto erano di tipo pratico; non esisteva però un quadro teorico più generale nel quale inserirli.

È nell'antica Grecia, attorno al 7° secolo a.C., che la geometria diventa una vera scienza, anzi la scienza per eccellenza. Il primo artefice di questa trasformazione è stato Talete di Mileto. Non abbiamo suoi scritti, ma gli antichi filosofi greci attribuiscono a lui risultati notevoli: previde un'eclissi solare, misurò l'altezza della piramide di Cheope e, soprattutto, invitò a studiare le proprietà geometriche fondamentali in astratto, anche se inizialmente poteva sembrare un'attività inutile.

L'altro personaggio chiave della trasformazione della geometria in scienza fu Euclide, nato ad Alessandria d'Egitto nel 4° secolo a.C. Anche della sua vita si sa poco, ma in compenso è rimasta la sua opera principale, Gli elementi, che per molti secoli è stato uno dei libri più studiati, un modello di come si costruisce una scienza deduttiva. Euclide parte da poche nozioni comuni e da proprietà che tutti possono accettare, i postulati, e grazie a essi dimostra con rigore tutte le altre proposizioni, che diventano teoremi. Euclide fonda il metodo ipotetico-deduttivo, basato su poche ipotesi iniziali e molte deduzioni (cioè dimostrazioni) e che da allora in poi è diventato il metodo principale per 'fare' matematica.

Geometria descrittiva

Quando si vuole disegnare un paesaggio o una scena ambientata in una città si pone un problema geometrico non semplice: quello di rappresentare sul piano del foglio, in due dimensioni, ciò che in realtà appartiene allo spazio tridimensionale. Si pone quindi il problema di riprodurre la realtà circostante così come la vede il nostro occhio.

Il problema era già stato affrontato e in qualche modo risolto nell'antichità. Euclide sottolineava che per noi le rette parallele non sono mai tali (come può confermare una fotografia scattata ai binari del treno).

Tuttavia nel corso del Medioevo si persero, anche per motivi culturali, le tecniche che pittori e artigiani possedevano per dare l'illusione della profondità e solo con il Rinascimento, nel 15° secolo, in Italia, il problema venne risolto in modo rigoroso. Figure di artisti e matematici, come Filippo Brunelleschi, Leon Battista Alberti e Piero della Francesca, scoprirono le leggi matematiche della prospettiva e le applicarono rigorosamente nelle loro opere.

Un esempio è il corridoio di colonne dipinto da Piero della Francesca intorno al 1470 e appartenente al polittico di Sant'Antonio. Il metodo adottato dall'artista per realizzare il dipinto può essere così illustrato. Supponiamo di voler riprodurre in prospettiva un quadrato ABCD, che può rappresentare, in modo semplificato, il pavimento di una stanza. Si segna un punto O a una certa distanza da un lato del quadrato (che rappresenta la linea di terra); la distanza di O dal quadrato rappresenta l'altezza da terra del punto da cui si osserva (l'altezza degli occhi); per O si conducono i segmenti che, in prospettiva, rappresentano i lati paralleli del quadrato e che nella realizzazione prospettica non risultano più paralleli. Per il punto O si traccia poi la retta parallela al lato CD e, su tale retta, si considera un punto K: la distanza tra O e K rappresenta la distanza dell'osservatore dalla linea di terra CD. Unendo K con D si viene a formare la diagonale del quadrato visto in prospettiva. Si possono ora tracciare le linee parallele a distanza progressivamente minore: si formano così trapezi che rappresentano, sempre in prospettiva, le mattonelle quadrate del pavimento.

L'algebra in aiuto della geometria

Il mondo dei numeri, l'aritmetica, e quello delle figure, la geometria, sono rimasti divisi per secoli. Solo a partire dal Seicento, con il filosofo e matematico francese Cartesio, questi mondi si avvicinano con la nascita della geometria analitica. Un risultato di tale incontro tra numeri e figure sono i grafici che oggi comunemente incontriamo nei giornali e in televisione: sono fatti di linee, rettangoli, oggetti geometrici, ma servono per descrivere dati numerici. L'idea di fondo è quella di 'chiamare' i punti del piano con due numeri, le coordinate cartesiane che li individuano.

Il metodo è semplice ed è analogo a quello che si usa per identificare, con la latitudine e la longitudine, un punto sulla superficie terrestre (coordinate geografiche). Roma, per esempio, si trova a quasi 42° a nord dell'Equatore e a circa 12° e mezzo a est del meridiano di Greenwich e la sua posizione su una carta geografica è individuata da questi due numeri. Fissate infatti due rette nel piano, gli assi cartesiani, ogni punto viene individuato dalle sue coordinate rispetto a esse. Per esempio, quello nel punto di coordinate (3;2): la coordinata orizzontale, chiamata ascissa, è 3; quella verticale, chiamata ordinata, è 2. Con questo metodo non solo a ogni punto viene associata una coppia di numeri, ma ogni curva che si possa disegnare sul piano può essere descritta da un oggetto algebrico, un'equazione.

Trasformazioni geometriche

Quando si afferma che due figure sono uguali non si è ancora detto tutto. Quali, per esempio, tra la figure qui illustrate sono uguali?

Sono certamente 'uguali' i triangoli A e D perché è possibile spostare A in modo da sovrapporlo esattamente al triangolo D. Ma anche C è uguale ad A e D: solo che è simmetricamente uguale e non si può sovrapporre agli altri. Il triangolo B, invece, non ha le stesse dimensioni di A: è però uguale per forma, è simile ‒ come si dice ‒ ad A. Infine, il rettangolo E è certamente diverso come forma da A: tuttavia, poiché ha la base uguale a quella di A e la sua altezza ne è la metà, la sua area risulta uguale a quella di A, secondo una nota regola della geometria elementare.

In geometria occorre perciò spesso spostare l'attenzione dall'idea di uguaglianza alle trasformazioni che permettono di passare da una figura all'altra. Per esempio, per ingrandire o rimpicciolire si può proiettare una figura da un punto O, oppure, per costruire la simmetrica di una figura, si possono tracciare punti dall'altra parte di una retta r alla stessa distanza da essa. Trasformazioni quali le traslazioni, le rotazioni o le simmetrie si trovano spesso in natura. E spesso si trovano forme che sono simili a loro stesse e sono chiamate frattali. A partire da un triangolo e costruendo ogni volta su ogni lato una nuova 'punta' a triangolo si forma una figura nota come il fiocco di neve di Koch.

Anche le trasformazioni geometriche possono essere descritte da equazioni. Per esempio, se si trasla una figura orizzontalmente, di 10 cm, ogni suo punto avente come ascissa un numero x si sposta e avrà come ascissa il numero x+10. Il vantaggio della descrizione attraverso le coordinate è che le soluzioni di una equazione sono facilmente calcolate da un computer. Rotazioni, ingrandimenti e anche movimenti più complessi possono essere descritti e riprodotti da un computer ed è così che oggi vengono prodotti e disegnati molti disegni animati.

Dalla geometria alle geometrie

Naturalmente la geometria non riguarda soltanto le figure del piano, ma anche i solidi e la descrizione dello spazio tridimensionale. Alle coordinate per lunghezza e larghezza basta aggiungerne un'altra per l'altezza e così si individua ogni punto dello spazio. Ma la geometria va oltre la descrizione dello spazio fisico. Tre coordinate, oltre a individuare un punto dello spazio, sono utilizzate per identificare un colore sul monitor di un computer. Ogni colore è identificato da tre numeri, a seconda di come si mescolano i tre colori fondamentali (che sono come gli assi del riferimento): il rosso, il verde e il blu.

L'applicazione a numerosi problemi, i diversi modi di vedere lo spazio, l'interpretazione geometrica di fatti non geometrici quali i colori, le diverse impostazioni con equazioni o senza, la prospettiva, l'attenzione alle trasformazioni fanno sì che oggi non si parli più di geometria ma di geometrie, perché ve ne sono diverse varietà. Esistono anche geometrie ‒ come la topologia, una branca di questa disciplina ‒ per le quali non interessano le misure; e ci sono geometrie, dette geometrie non euclidee, in cui non vale uno dei postulati di Euclide. Si tratta del postulato della parallela, per il quale da un punto si può condurre una sola retta parallela a una retta data.

L'altezza della piramide

Il problema dell'altezza della piramide può servire a spiegare il nesso tra proprietà generali e problemi particolari in geometria. Supponiamo di voler misurare un campanile e di avere a disposizione un bastoncino di lunghezza conosciuta, per esempio 1 m. A una determinata ora di un giorno assolato disponiamo il bastoncino in verticale e misuriamo la lunghezza della sua ombra. Misuriamo quindi anche la lunghezza dell'ombra del campanile. Per capire meglio la situazione possiamo disegnare due triangoli (che non esistono nella realtà, ma solo nella nostra mente).

Poiché i raggi del Sole sono paralleli, i due triangoli hanno gli angoli di uguale ampiezza e quindi i lati sono in proporzione. Per esempio, se l'ombra del bastoncino è lunga la metà del bastoncino stesso, anche l'ombra del campanile è la metà dell'altezza del campanile. Così, misurando la sua ombra possiamo ricavare la sua altezza.

Due triangoli come i precedenti, con tutti gli angoli uguali, vengono chiamati simili e proprio l'uguaglianza e la similitudine sono state studiate con attenzione dai Greci: in astratto, senza pensare a un loro uso pratico.

Sulla misura del raggio terrestre

Nel 3° secolo a.C. il matematico Eratostene, che dirigeva la biblioteca di Alessandria d'Egitto, all'epoca la più grande del mondo, misurò la lunghezza del meridiano terrestre con un semplice strumento, lo gnomone, per esempio un obelisco di altezza nota. Egli sapeva che nella città di Siene (l'attuale Assuan) i raggi del Sole, a mezzogiorno del 21 giugno, cadono esattamente perpendicolari perché non producono alcuna ombra; nello stesso giorno, ad Alessandria, misurò l'ombra dello gnomone sul terreno. Da questa misura ricavò l'ampiezza dell'angolo che i raggi del Sole formavano ad Alessandria rispetto alla verticale. Trovò così un angolo di 7,2°: poiché questo valore è la cinquantesima parte dell'angolo giro, Eratostene dedusse che la lunghezza del meridiano terrestre doveva essere cinquanta volte la distanza tra Alessandria e Siene. Questa distanza era nota e uguale a circa 800 km attuali. La circonferenza della Terra doveva quindi essere di 800×50=40.000 km, un valore molto vicino a quello reale poi calcolato con strumenti molto più sofisticati.

L'equazione di una retta

Tutti i punti segnati in colore nel disegno sono quelli per i quali la coordinata verticale (y) è uguale al doppio della coordinata orizzontale (x). Si può affermare che la retta alla quale appartengono tutti questi punti è formata da punti per i quali y=2x. La retta (oggetto geometrico) è così descritta da una equazione (oggetto algebrico).

Flatlandia: un mondo a due dimensioni

Nel 1882 il reverendo Edwin A. Abbott pubblica un racconto, Flatlandia, in cui descrive un mondo piatto (flat, in inglese), a due dimensioni. È un mondo abitato da segmenti, poligoni, cerchi, tutti suddivisi in classi sociali in base alla maggiore o minore regolarità: dai regolarissimi Cerchi (i sacerdoti) ai nobili Poligoni, scendendo poi ai Quadrati (la classe media), ai Triangoli (gli operai). Le donne sono collocate al gradino più basso della scala sociale e hanno quindi la forma di Segmenti: ma proprio per questo sono particolarmente aguzze e temibili e, se camminassero senza ancheggiare un po', da dietro si potrebbero appena intravedere solo come punti. Gli abitanti di Flatlandia non hanno idea della terza dimensione, non possono vedere 'dall'alto' il loro piatto mondo e si stupiscono quando ai loro occhi compare un punto che si allarga sempre più per poi rimpicciolirsi, diventare di nuovo un punto e sparire. Non possono capire che si tratta di una sfera tridimensionale che ha attraversato il loro mondo piatto.