poligonale
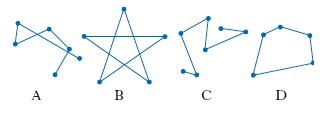
In geometria, linea p. (e più spesso p.), linea spezzata, cioè sequenza finita di segmenti del tipo A1A2, A2A3, A3A4, …, An–1An: questi segmenti sono detti lati della p. e sono quindi disposti in modo tale che ciascuno (esclusi il primo e l’ultimo) abbia un estremo in comune con il segmento precedente e l’altro estremo in comune con il segmento successivo; una p. è chiusa se An coincide con A1, aperta in caso contrario; è non intrecciata se non vi sono altri punti in comune fra i lati (fig. 1).
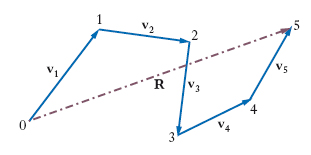
P. dei vettori Nella teoria dei vettori è una p., in generale sghemba, mediante la quale si determina il risultante di un sistema di vettori (in particolare di un sistema di forze) v1, v2, …, vn. Si costruisce nel modo seguente: scelto ad arbitrio nello spazio un punto o si applica in esso il vettore v1, nel suo estremo libero 1 si applica v2, nell’estremo libero di questo, 2, si applica v3, e così di seguito. Il vettore R che chiude tale p. (fig. 2), e che risulta indipendente dall’ordine dei vettori, ha appunto il nome di risultante, o somma geometrica, del sistema dato.