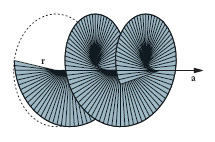
elicoide
Superficie generata da una curva indeformabile assoggettata a un moto elicoidale uniforme, composto di un moto uniforme di rotazione intorno a un asse fisso e di un moto di traslazione uniforme parallelo all’asse stesso. All’e. appartengono così infinite eliche circolari di uguale asse, passo e verso (asse, passo e verso dell’e.): le traiettorie dei punti della curva nel moto suddetto. Se la curva generatrice incontra l’asse in un punto, l’asse appartiene per intero all’e., che si dice allora chiuso (e in caso contrario aperto); se la curva generatrice è una retta, essa può essere normale all’asse ( e. rigato retto) oppure no ( e. rigato obliquo). Tra gli e. rigati ricordiamo: l’ e. sviluppabile, luogo delle tangenti a una data elica circolare; l’ e. chiuso retto (v. fig.), generato da una retta r incidente all’asse a e perpendicolare a esso, che non è poi altro che la superficie della scala a chiocciola e della vite a filetto rettangolare (immaginate prolungate indefinitamente); l’ e. chiuso obliquo (generatrice incidente all’asse, ma non perpendicolare a esso), che è poi la superficie della vite a filetto triangolare. Tra gli e. cerchiati (generati cioè dal moto elicoidale di un cerchio) ricordiamo: la colonna torta, che è l’e. generato da un cerchio giacente in un piano perpendicolare all’asse; la vite di Saint-Gilles, che è l’e. generato da un cerchio giacente in un piano passante per l’asse; il serpentino, che è l’e. generato da un cerchio il cui piano si mantenga sempre ortogonale all’elica descritta dal centro del cerchio medesimo.