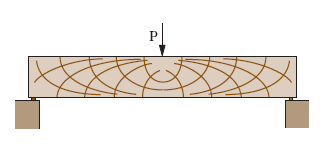
isostatiche, linee
Nei sistemi elastici piani, linee del piano del sistema tali che in ogni loro punto la tangente alla curva ha la direzione di una delle due tensioni principali relative al punto medesimo. Per ogni punto del sistema piano passano due linee i., tra loro ortogonali, corrispondenti al valore minimo e massimo della tensione normale e al valore nullo della tensione tangenziale (direzioni principali), sì che nel complesso l’insieme delle linee i. è costituito da due famiglie di curve mutuamente ortogonali la cui configurazione è caratteristica per ogni regime di sollecitazione (v. fig.). Corrispondendo, per lo più, la tensione massima a uno sforzo di trazione e la minima a uno sforzo di compressione, si parla anche di isostatiche di trazione e di compressione, ma non è escluso che per un punto passino due linee i. entrambe di trazione o di compressione e che una medesima linea i. possa passare da valori di trazione a valori di compressione e viceversa. È chiaro che il valore della tensione è diverso da punto a punto anche su di una medesima linea isostatica. Il tracciamento delle linee i. si può effettuare per inviluppo, dopo aver determinato le direzioni principali di tensione in un sufficiente numero di punti del piano, ricorrendo a tale scopo, per es., al cerchio di Mohr (➔ Mohr, Christian Otto), oppure utilizzando le linee isocline, ricavabili con i metodi della fotoelasticità piana.
La configurazione delle linee i. fornisce una chiara indicazione del funzionamento statico di una struttura piana, rappresentando esse, per così dire, le linee preferenziali secondo cui si trasmettono le tensioni interne. In particolare, nel caso di strutture in cemento armato le i. di trazione forniscono le linee di disposizione ideale per le armature metalliche. Qualora si passi a considerare un sistema elastico tridimensionale (anziché piano), per ogni punto si hanno tre direzioni principali di tensione (mutuamente ortogonali), caratterizzate dall’annullarsi della corrispondente tensione tangenziale. Si denominano in questo caso superfici isostatiche le tre famiglie di superfici definite dall’inviluppo delle corrispondenti direzioni principali considerate per tutti i punti del sistema.