omotetia
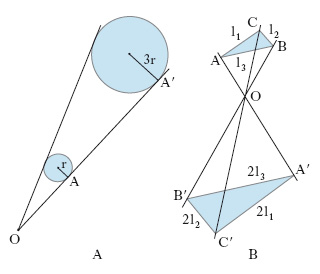
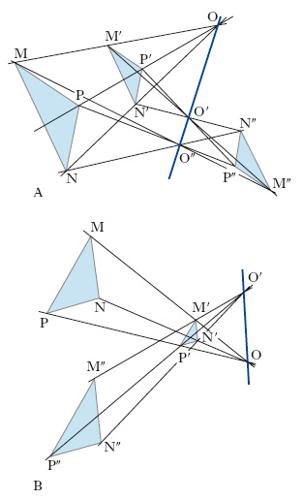
In matematica, particolare omografia tra due spazi affini o euclidei n-dimensionali sovrapposti (in particolare, per n=2 o 3, tra due piani o due spazi tridimensionali ordinari), nella quale esiste un unico punto proprio unito O, centro dell’o., e ogni retta è parallela alla retta corrispondente. Da ciò segue che punti corrispondenti sono allineati con O e che il rapporto tra due segmenti corrispondenti A′B′: AB, detto rapporto di o., è costante; l’angolo di due rette è uguale all’angolo delle rette corrispondenti e figure corrispondenti sono simili e similmente disposte. Sono anche costanti sia il rapporto di aree sia quello di volumi, sia, più in generale, quello tra estensioni m-dimensionali con m≤n: tale rapporto è uguale alla m-esima potenza del rapporto di omotetia. In fig. 1 sono indicate due o. i cui rapporti valgono, rispettivamente, k=3 e k=−2. Il prodotto di due o. di centri O e O′ (fig. 2A) è una nuova o., il cui centro O″ è allineato con O e O′ e il cui rapporto k″ è uguale al prodotto kk′ (in fig., k=1/2, k′=−1, k″=−1/2); se, però, kk′ è uguale a 1, il prodotto delle due o. non è un’o. ma una traslazione parallela alla retta OO′ (fig. 2B).