scacchi
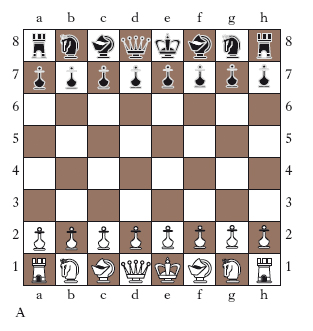
scacchi - Gioco da tavolo fondato su strategia e abilità logica, nel quale due giocatori muovono 16 pezzi ciascuno (s., da cui il nome del gioco), bianchi per l’uno e neri per l’altro, su un quadrante diviso in 64 caselle (scacchiera), allo scopo di catturare il pezzo principale dell’avversario, il re, con una mossa detta s. matto. Gli altri pezzi rappresentano 1 donna, 2 torri, 2 alfieri, 2 cavalli e 8 pedoni (fig. 1A, B).
Gioco antichissimo, di probabile origine indiana, si diffuse poi nella Persia sasanide e tra gli Arabi, che lo importarono nell’Europa occidentale, dove appare conosciuto già alla metà dell’11° secolo. Alla fine del 15° sec. si fissarono le regole ancora oggi in uso. Dalla seconda metà del 19° sec. si sono organizzati campionati del mondo che hanno visto protagonisti grandissimi campioni: tra questi il cubano J.R. Capablanca (1888-1942), il tedesco E. Lasker (1868-1941), il russo A. Alekhine (1892-1946), fino ai più recenti, i russi G. Kasparov (n. 1963) e il suo allievo V. Kramnik (n. 1975), l’indiano V. Anand (n. 1969), il bulgaro V. Topalov (n. 1975).
Le organizzazioni scacchistiche nazionali (in Italia: la Federazione Scacchistica Italiana, FSI), sono riunite nella FIDE (Fédération Internationale Des Échecs), che conta oltre 150 nazioni affiliate e che ha codificato le norme per il gioco universalmente seguite; nel 1993 si è registrata una scissione, con la creazione della Professional Chess Association (PCA) per opera di Kasparov.
Il gioco degli scacchi si ricollega, sotto l’aspetto matematico, alla teoria dei grafi e molti dei problemi classici riguardanti gli s. sono in effetti problemi particolari sui grafi. Tutte le possibili partite di s. si possono riassumere e visualizzare in un solo grafo, anzi in un albero; l’unica radice R dell’albero degli s. rappresenta la situazione iniziale della scacchiera, mentre gli spigoli che partono da R indicano le mosse possibili del Bianco e i loro estremi le situazioni dopo la prima mossa, e così via. In generale, da ogni vertice escono tanti spigoli quante sono le possibilità di gioco a partire dalla situazione schematizzata dal vertice stesso. Poiché ogni partita di s. si decide, in base alle regole di gioco, dopo un numero finito (anche se a volte molto grande) di mosse, si ha per conseguenza che l’albero degli s. è finito. A ogni partita di s. corrisponde un cammino, nell’albero, che va dalla radice R fino a un punto terminale. Una parte dei punti terminali rappresenta vittoria del Bianco, una parte vittoria del Nero e una parte un esito di parità. Scopo di un giocatore è di trovare un cammino nell’albero del gioco che, partendo da un dato punto, possa condurre, nonostante le mosse dell’avversario, a un punto terminale a lui favorevole.
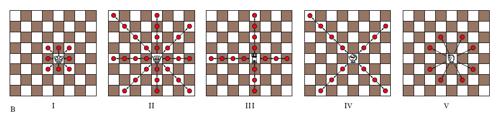
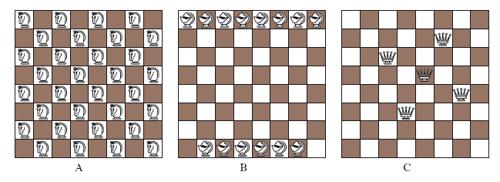
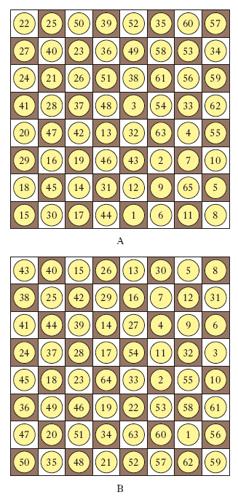
Il gioco degli s. ha dato origine a un certo numero di problemi, alcuni dei quali di difficile soluzione, che si possono anch’essi inquadrare nell’ambito della teoria dei grafi. Fra questi: a) determinare il numero massimo di pezzi di uno stesso tipo (per es., Cavalli o Alfieri o Donne) che si possono collocare sulla scacchiera in modo che tutte le caselle libere siano ‘controllate’ ma senza che due pezzi siano in presa; b) medesimo problema ma in relazione al numero minimo di pezzi; c) problema del salto del Cavallo. Per quanto riguarda il problema a) la soluzione è 32, 14, 12 a seconda che si considerino i Cavalli, gli Alfieri (fig. 2A, B) o le Donne rispettivamente. Il caso delle Donne è il più celebre: piazzare 8 donne e trovare tutte le soluzioni; C.F. Gauss credette che esistessero 76 soluzioni, il numero esatto è invece 92. Per il problema b), sempre riguardo alle Donne, la soluzione è 5 (fig. 2C). Il problema c) è celeberrimo e consiste nel far percorrere al Cavallo tutte le caselle con 63 salti consecutivi; se ne occuparono probabilmente gli antichi matematici indiani, e in seguito A. De Moivre, L. Eulero ecc.; esso ammette un numero enorme, imprecisato, di soluzioni. Una prima classificazione porta a distinguere le soluzioni in chiuse, quando il Cavallo con un ultimo salto può tornare nella casella iniziale (fig. 3A, dove le successive posizioni del Cavallo sono numerate) e aperte, nel caso contrario (fig. 3B).