grafo

Nel linguaggio scientifico, struttura relazionale formata da un insieme finito di oggetti detti nodi o vertici, e da un insieme di relazioni tra coppie di oggetti dette archi o spigoli. Per indicare un g. viene utilizzata una notazione del tipo: G(N, A), dove N indica l’insieme dei nodi e A l’insieme degli archi. Se vengono indicati con i e j due nodi del g., un arco che congiunge i a j viene spesso indicato con la notazione (i, j).

È, per es., possibile rappresentare come un g.: una rete telefonica in cui i nodi rappresentano gli utenti e i punti di smistamento e gli archi i cavi di collegamento tra i nodi; un circuito elettrico in cui i nodi rappresentano i punti di giunzione e gli archi i collegamenti elettrici; una rete stradale in cui i nodi rappresentano gli incroci e gli archi le strade; un impianto idraulico in cui i nodi rappresentano le giunzioni e gli archi i tubi; una rete di elaboratori in cui i nodi rappresentano gli elaboratori connessi in rete e gli archi le linee di comunicazione tra di essi; un programma di calcolo in cui i nodi rappresentano le istruzioni ed esiste un arco tra due nodi se le relative istruzioni possono essere eseguite nel programma in successione; una struttura dati in cui i nodi rappresentano i dati e gli archi i legami tra i dati realizzati tramite puntatori. Nel caso di un programma di calcolo o di una rete stradale, in cui tutte le strade sono a senso unico, gli archi del g. potranno essere percorsi in una sola direzione; nel caso invece di una rete idraulica i collegamenti sono tipicamente bidirezionali (a meno che nell’impianto esistano valvole).

Sviluppi della teoria dei grafi

fig. 1

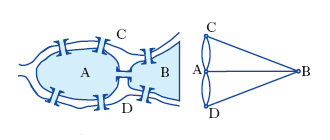
L’origine storica della teoria del g. è in genere fatta risalire a una memoria di L. Eulero del 1736, nella quale veniva formulato il famoso problema dei sette ponti di Königsberg: attraverso Königsberg scorre il fiume Pregel e, in mezzo al fiume, vi sono due isole (che indichiamo con A e B e le due rive del fiume con C e D; fig. 1), collegate fra loro da un ponte; inoltre quattro ponti (due per parte) collegano l’isola A alle due rive e due ponti (uno per parte) collegano l’isola B alle due rive; il problema consiste nel decidere se sia possibile, partendo da un qualsiasi punto, camminare attraverso ogni ponte esattamente una volta, ritornando al punto di partenza. Eulero, per dimostrare che il problema non ammette soluzione, rimpiazzò ogni riva del fiume e ogni isola con un nodo di un g., e ogni ponte con un arco fra i nodi corrispondenti alle due entità collegate dal ponte. In questo modo, dimostrare che il problema non ammette soluzione equivale a dimostrare che il g. non ammette un ciclo che passa esattamente una volta su ogni arco (ciclo euleriano). Il teorema di Eulero afferma che condizione necessaria e sufficiente affinché un g. sia percorribile nel modo richiesto è che esista un percorso fra ogni coppia di nodi e tutti i nodi siano toccati da un numero pari di archi. Si può vedere nel caso in esame che la prima condizione è verificata, ma i quattro nodi sono tutti toccati da un numero dispari di archi. Il teorema non risolve solo il problema specifico descritto sopra, ma fornisce un criterio generale per decidere se un qualsiasi g. è percorribile nel modo richiesto. Nel 1759 Eulero scrisse un’altra importante memoria sulla teoria dei g. definendo, fra l’altro, il problema del ciclo hamiltoniano, ossia del ciclo che passa esattamente una volta per tutti i nodi di un grafo.

Nel 1771 anche A.-T. Vandermonde trattò il problema del ciclo hamiltoniano. Nell’Ottocento vennero sviluppati importanti capitoli della teoria dei g.: nel 1813 A.-L. Cauchy enunciò in termini di g. alcuni problemi; su poliedri nel 1840 A.F. Möbius formulò la congettura dei 4 colori; nel 1847 G.R. Kirchhoff sviluppò la teoria delle reti elettriche; nel 1856 W.R. Hamilton elaborò alcuni procedimenti di calcolo basandosi su g. e T.P. Kirkman studiò alcune proprietà dei cicli hamiltoniani; nel 1875 e nel 1878 A. Cayley e J.J. Sylvester svilupparono alcuni aspetti della teoria dei g. per lo studio degli isomeri chimici; nel 1880 e nel 1890 A.B. Kempe e P.J. Heawood formularono in modo rigoroso il problema dei 4 colori e ne risolvettero alcuni aspetti; nel 1882 E. Lucas pubblicò un libro di giochi matematici in cui viene descritto un algoritmo del matematico francese E.-M. Trémaux per uscire con sicurezza da un labirinto, oggi usato comunemente come procedura di visita di un g.; nel 1891 G. Brunel analizzò reti elettriche con tecniche di teoria dei g. e J. Peterson studiò i g. regolari; nel 1895 G. Tarry proseguì nello studio dei labirinti.

Nel corso del Novecento sono state sviluppate numerose elaborazioni e applicazioni basate sulla teoria dei grafi. Fra i risultati più significativi ricordiamo: nel 1900 il trattato di H. Pointcaré, Sécond complément à l’analysis situs; nel 1926 A. Sainte-Laguë studiò problemi di cammino ottimo e K. Kuratowski trovò una caratterizzazione completa dei g. planari; nel 1935 P. Hall affrontò alcuni problemi di matematica combinatoria legati ai g.; G. Polya ricollegò le caratteristiche di alcuni g. a relazioni chimiche, e H. Whitney a sistemi di equazioni lineari; nel 1936 D. König scrisse il primo trattato sistematico sui g. e, insieme a J. Egervàry, trovò importanti proprietà; nel 1937 A.W. Tuker sviluppò ulteriormente alcuni problemi di cammino ottimo; nel 1940 G.B. Dantzig, che più tardi proporrà il metodo del simplesso per risolvere problemi di programmazione lineare, affrontò alcuni problemi di assegnamento su g.; nel 1944 J.L. von Neumann con O. Morgenstern pubblicò un trattato di teoria dei giochi utilizzando concetti di teoria dei g.; nel 1946 G. Birkhoff analizzò gli alberi e W.T.T. Tutte i cicli hamiltoniani; nel 1954 S. Johnson studiò i problemi di sequenziamento e, con G. Dantzig e D.R. Fulkerson, riprese il problema del ciclo hamiltoniano ottimo, detto problema del commesso viaggiatore; nel 1955 H.W. Kuhn studiò i sistemi di disequazioni lineari; nel 1956 L.R. Ford e D.R. Fulkerson scrissero un trattato sulle reti di flusso e sui cammini su g.; nel 1957 T.C. Koopmans (che nel 1975 per questi studi riceverà insieme a L.V. Kantorovič il premio Nobel per l’economia) analizzò i problemi di trasporto e di assegnamento; nel 1958 C. Berge scrisse un trattato di teoria dei g.; nel 1961 P. Erdös cominciò a pubblicare importanti studi su classi di problemi su g. che sarebbero proseguiti per tre decenni; nel 1962 R.E. Bellman introdusse le tecniche di programmazione dinamica; nel 1966 R. Gomory studiò le reti di comunicazione; nel 1970-72 S.A. Cook, J. Edmonds e R.M. Karp costruirono le basi della teoria della complessità; nel 1979 L. Lovász dimostrò la congettura dei g. perfetti di Berge.

Lo sviluppo e la diffusione di queste metodologie è dovuto principalmente al parallelo sviluppo dei mezzi di elaborazione. Il motivo dell’interesse dell’informatica per i modelli combinatori in generale, e la teoria dei g. in particolare, è evidente, in quanto i sistemi digitali di calcolo sono sistemi discreti e quindi rappresentabili con g.; i circuiti logici che presiedono al funzionamento di un elaboratore sono anch’essi rappresentabili con g., e così le strutture dati usate in un elaboratore, le interconnessioni in rete di elaboratori e i sistemi di comunicazione. La logica di funzionamento di un sistema di elaborazione è di norma di tipo discreto e rilevanti applicazioni dell’informatica, quali le basi di dati, hanno ugualmente una struttura di tipo essenzialmente discreto.

Tipi di grafi

fig. 2A

fig. 3A

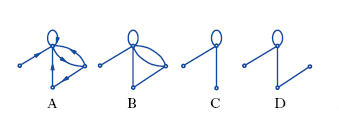
G. orientato G. in cui gli archi rappresentano relazioni tra coppie ordinate di nodi. In questo caso gli archi hanno una ‘testa’ o nodo di arrivo e una ‘coda’ o nodo di partenza (fig. 2A); se invece le relazioni sono tra coppie non ordinate, il g. è detto non orientato. Un nodo i di un g. orientato è detto predecessore di un nodo j se esiste un arco diretto da i a j; è detto successore di j se esiste un arco diretto da j a i. Multigrafo G. in cui esistono più archi fra la stessa coppia di nodi (fig. 2B), oppure fra una stessa coppia ordinata. Sottografo, g. parziale e copertura di un g. Dato un g. non orientato G(N, A) e un g. non orientato H(V, E) con V appartenente a N ed E appartenente a A, tale che gli archi di E sono tutti gli archi di A aventi entrambi i nodi terminali nell’insieme V, H è detto sottografo di G (fig. 2C). Se invece E è formato solo da un sottoinsieme degli archi di A con entrambi i nodi terminali nell’insieme V, allora H è detto g. parziale di G (fig. 2D). Si dice che un g. G ‘copre’ un altro g. H, se H è un g. parziale di G. G. connesso G. in cui per ogni coppia di nodi esiste un percorso che li congiunge (fig. 3A). Nel caso di g. orientati, se esiste un cammino fra ogni coppia di nodi, si dice che il g. è fortemente connesso (fig. 3B); se esiste solo un cammino non orientato fra ogni coppia di nodi, si dice che il g. è debolmente connesso (fig. 3C). Un sottografo di un g. G connesso e tale che non esistano archi di G tra i nodi del sottografo e i nodi non appartenenti al sottografo è detto componente connessa di G. Un nodo i di un g. non orientato è detto adiacente a un nodo j se esiste l’arco (i, j); se il nodo non ha nodi adiacenti è detto isolato; se l’arco (i, j) esiste, esso è detto incidente sui nodi i e j. Due archi con almeno un nodo in comune sono detti archi adiacenti. Un g. (orientato o non orientato) tale che per ogni coppia (i, j) esiste un arco è detto completo (fig. 3D). Un g. orientato G(N, A) tale che se (i, j) appartiene ad A allora anche (j, i) appartiene ad A è detto simmetrico (fig. 3E). Se invece per ogni coppia non ordinata (i, j) esiste al più uno solo dei due archi (i, j) e (j, i), allora il g. è detto antisimmetrico. Dato un g. G(N, A) non orientato, un sottoinsieme di nodi S appartenente a N tale che il sottografo indotto sia privo di archi è detto insieme stabile, o anche insieme indipendente. Se invece il sottografo indotto da S forma un g. completo è detto clique. La cardinalità di un insieme stabile con il massimo numero di nodi è detta numero di stabilità del g.; la cardinalità della clique con il massimo numero di nodi è detta numero di clique del grafo. G. bipartito G. in cui l’insieme N dei nodi può essere diviso in due parti S e T tali che non esistono archi con entrambi i nodi terminali in S, né archi con entrambi i nodi terminali in T; tutti gli archi hanno quindi un nodo terminale in S e uno in T (fig. 3F). Un g. è bipartito se e solo se non ha cicli con un numero dispari di archi. G. planare G. che è possibile disegnare su di un piano senza che gli archi debbano intersecarsi. Se un g. contiene un sottografo completo di 5 nodi, spesso indicato con la notazione K₅ (fig. 3G), o un sottografo bipartito completo di 6 nodi con 3 nodi in ognuna delle due parti, spesso indicato con la notazione K_3,3 (fig. 3H), allora non può essere planare.

Cammino su grafo

In un g. non orientato è un insieme ordinato di archi (a₁, a₂, a₃, ..., a_n). In un g. orientato vi sono due tipi di cammini: il primo, chiamato cammino non orientato, o anche catena, non pone vincoli sull’orientamento degli archi; il secondo tipo, detto semplicemente cammino, richiede che la sequenza di archi sia tale che la testa di un arco coincida con la coda del successivo, vale a dire che sia possibile percorrere il cammino seguendo sempre il verso di percorrenza degli archi. Se un cammino non passa mai due volte per lo stesso nodo è detto cammino elementare, se non passa mai due volte per lo stesso arco è detto cammino semplice. Ciclo di un g. È un cammino tale che il nodo di partenza e quello di arrivo coincidono. Se il ciclo non passa mai due volte per lo stesso nodo è detto ciclo elementare. Nel caso di g. orientati, un ciclo formato da archi orientati in entrambi i due possibili versi di percorrenza è detto ciclo non orientato. Dato un g. o un multigrafo (orientato o non orientato), un ciclo che passa esattamente una volta per ogni arco è detto ciclo euleriano, un ciclo che passa esattamente una volta per ogni nodo è detto ciclo hamiltoniano. Un g. che ammette un ciclo euleriano è detto g. euleriano (fig. 3I). Un g. che ammette un ciclo hamiltoniano è detto hamiltoniano (fig. 3L). Condizione necessaria e sufficiente affinché un g. connesso non orientato sia euleriano è che tutti i suoi nodi abbiano grado pari (teorema di Eulero, 1736). Un g. orientato privo di cicli è detto aciclico. Nel caso di g. non orientati, sorge il problema che, potendo percorrere un arco in entrambi i sensi, un singolo arco forma un ciclo. Per evitare tale paradosso, in genere si vincola il ciclo a non utilizzare mai due volte uno stesso arco. Si definisce quindi ciclo una sequenza ordinata di archi distinti, tale che il nodo di partenza e quello di arrivo coincidono.

Grado, centro, raggio e diametro del grafo

Dato un g. non orientato, il numero di archi incidenti su di un dato nodo è detto grado del nodo. Se in un g. tutti i nodi hanno lo stesso grado k, il g. è detto regolare di grado k; se inoltre k=3, il g. è detto cubico. Per i g. orientati si può definire un grado di ingresso del nodo i come numero di archi entranti in i, e un grado di uscita di i come numero di archi uscenti. Dato un g. G(N, A) non orientato, sia d(i, j) il numero minimo di archi necessario per costruire un cammino da i a j. Si dice diametro del g. la quantità D=max d(i, j). Si dice centro del g. il nodo (o i nodi) per cui è minima la quantità R(i)=max_j d(i, j). Se k è il nodo centro (o uno dei nodi centrali) del g., il valore R(k) è detto raggio del grafo.

Albero di un grafo

È un g. non orientato connesso e senza cicli (o anche, in modo del tutto equivalente, un g. connesso e senza cicli); un g. connesso con n nodi e n−1 archi; un g. senza cicli con n nodi e n−1 archi; un g. senza cicli tale che comunque si aggiunga un arco si crea un ciclo (e uno solo); un g. connesso tale che comunque si elimini un arco si ottiene un g. non connesso; un g. tale che per ogni coppia di nodi esiste esattamente un cammino che li collega. In un albero, i nodi di grado uguale a uno sono detti foglie. Scelto un nodo dell’albero, e denominato tale nodo radice, è possibile introdurre il concetto di livello di un nodo come il numero di archi che è necessario percorrere per raggiungere la radice (la radice ha quindi livello zero). Il livello più elevato è detto profondità dell’albero e dipende naturalmente dalla radice scelta. Togliendo da un albero uno o più archi si ottiene un insieme di alberi non connessi detto foresta. Nel caso di g. orientati valgono le stesse definizioni sostituendo ai termini ‘ciclo’ e ‘cammino’ le locuzioni ‘ciclo non orientato’ e ‘cammino non orientato’. Spesso, nel caso di g. orientati, gli alberi vengono denominati arbusti o arborescenze; l’equivalente di una foresta viene denominato boscaglia. Un albero in cui tutti i nodi hanno grado minore o uguale a tre, è detto albero binario (fig. 3M). Gli alberi binari sono di particolare importanza nelle applicazioni informatiche e nella ricerca operativa, in quanto molte strutture dati corrispondono ad alberi binari e in molti problemi applicativi è possibile memorizzare le soluzioni possibili nei nodi di un albero binario.

Colorazione di g. e numero cromatico

Una colorazione di un g. è una assegnazione di colori ai suoi nodi in modo tale che due nodi adiacenti (cioè fra i quali esista un arco) non siano mai colorati con lo stesso colore. L’insieme di tutti i nodi colorati con lo stesso colore è detta classe di colorazione. Una k-colorazione di un g. è una colorazione che usa k colori e suddivide quindi i nodi in k classi. Il numero cromatico di un g. è definito come il minimo k per cui esiste una k-colorazione del grafo. Uno dei più famosi problemi matematici rimasto aperto per oltre un secolo è il cosiddetto problema dei quattro colori (➔ colore), legato al problema della colorazione di carte geografiche. Secondo tale congettura ogni g. planare è 4-colorabile. Questa congettura, nota fino dagli inizi dell’Ottocento, è stata in seguito provata con tecniche enumerative, utilizzando in modo massiccio potenti calcolatori.