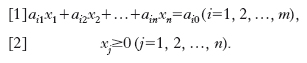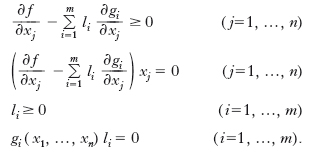programmazione

Economia

P. economica Il complesso degli interventi dello Stato nell’economia, realizzati spesso sulla base di un piano pluriennale (in questo senso il termine si alterna, nell’uso, con pianificazione). Nella terminologia corrente, e anche da parte di alcuni studiosi, si è però soliti distinguere tra pianificazione (➔) e p., tra piano e programma, riferendosi con il primo termine ai paesi socialisti e con il secondo ai paesi a economia di mercato. La storia della p. nelle economie di mercato descrive il processo attraverso il quale da una situazione, quale quella dei paesi occidentali nella seconda metà dell’Ottocento, in cui lo Stato aveva compiti estremamente circoscritti sul piano economico, si è passati a una situazione nella quale lo Stato svolge, o ci si auspica che svolga, un ruolo determinante nel processo di sviluppo.

La p. nei paesi a economia di mercato

Il fondamento teorico della p. nelle economie di mercato va ricercato innanzitutto nel pensiero di J.M. Keynes. Questi dimostrò che nel breve periodo il mercato lasciato a sé stesso può trovarsi in una situazione di equilibrio di non piena occupazione e che solo un certo ammontare di spesa pubblica improduttiva è in grado di portarlo al livello di piena occupazione. Dagli sviluppi della teoria keynesiana è risultato che il mercato non solo temporaneamente, cioè nel breve periodo, ma anche nel lungo periodo può trovarsi in situazione di non piena occupazione o può tendere alla stagnazione, sicché si dimostra indispensabile per il perseguimento dell’obiettivo della piena occupazione e dello sviluppo un certo ammontare di spesa pubblica produttiva, cioè di spesa pubblica volta a garantire indirettamente (per es. con le opere pubbliche), o direttamente (per es. con aziende produttive di proprietà pubblica), un certo livello di reddito. Quando l’intervento dello Stato nell’economia diventa un elemento determinante, sistematico, per il conseguimento di un determinato livello del reddito e dell’occupazione e di un determinato tipo di sviluppo (giacché questo è diverso a seconda di dove è occupata l’offerta di lavoro, cosa produce e con quali tecniche produce), la distinzione tra politica economica in generale e politica di piano diventa difficile.

Con riferimento al dibattito, che trae origine dal contributo di molti studiosi, quali per es. J.K. Galbraith, W. Leontief, J.A. Schumpeter, J. Tinbergen, si possono individuare due modi attraverso i quali si ritiene che la politica di piano, pur nel rispetto dei meccanismi di mercato, debba regolare il processo di sviluppo. Il primo suggerisce un’azione programmatica direttamente nel campo produttivo, sia attraverso la creazione di infrastrutture, sia attraverso la presenza di aziende produttive di proprietà pubblica, sia attraverso un’appropriata politica di incentivi creditizi, fiscali, doganali ecc., alle imprese produttive private. Il secondo suggerisce un’azione programmatica che punti prevalentemente sull’aumento dei consumi pubblici e sociali, quali la scuola, l’edilizia popolare e l’edilizia pubblica, l’assistenza sanitaria, il trasporto pubblico, la ricerca scientifica ecc. Secondo questo schema, una domanda pubblica programmata nel campo dei consumi è garanzia perché i meccanismi produttivi si mettano in moto, dal momento che è assicurato lo sbocco per la produzione. Evidentemente si tratta di due modelli alternativi, che come tutti i modelli danno una rappresentazione schematica di due linee antagoniste, ma che nella pratica comportano che, una volta sceltone uno come strategia dello sviluppo, non si escludano sul piano tattico alcuni elementi dell’altro.

Dal secondo dopoguerra, la p. economica è stata caratterizzata dallo sviluppo di strumenti econometrici in grado di fornire proiezioni corrette sul sistema produttivo, sul bilancio pubblico, sull’andamento del mercato finanziario e di individuare gli strumenti di politica economica necessari per il conseguimento dei risultati desiderati.

La p. a livello nazionale

Lo strumento della p. economica è stato ampiamente sfruttato nei paesi che adottano un’economia di mercato e i relativi obiettivi sono stati trasfusi in piani di attuazione, generalmente pluriennali. Nel Regno Unito il primo documento programmatico (White paper on employment policy) fu elaborato dal governo di coalizione nel 1944; negli anni 1947 e 1948 le linee di politica economica ebbero il loro fondamento negli Economic Surveys. Negli Stati Uniti, sotto la presidenza di F.D. Roosevelt, vi fu un importante esempio di p. economica territoriale con la creazione della Tennessee Valley Authority, ente territoriale federale di sviluppo, destinato a occuparsi del risanamento economico del bacino del fiume Tennessee. In Francia, nel 1947 fu varato il Piano Monnet (per il periodo 1947-53), frutto di una p. concertata tra rappresentanti dello Stato, delle imprese e dei lavoratori.

In Italia la politica di piano, come insieme coordinato di interventi di politica economica volti a correggere lo spontaneismo del mercato, fu prefigurata per la prima volta nel 1954 con lo Schema di sviluppo dell’occupazione e del reddito in Italia nel decennio 1955-1964 (Schema Vanoni) e nel 1967 fu costituito il Comitato Interministeriale per la Programmazione Economica (CIPE). La p. finanziaria, in Italia, è stata introdotta con la l. 468/5 agosto 1978, che prescrive alcuni atti di governo concernenti la finanza del settore pubblico allargato: il DPEF (Documento di programmazione economico-finanziaria), nel quale, ogni anno, il governo delinea le strategie pluriennali di politica economica, la legge finanziaria (➔ finanziaria, legge), la legge di bilancio annuale che deve contenere anche un bilancio pluriennale, il Rendiconto generale dello Stato (➔) e la legge di assestamento del bilancio annuale.

La p. a livello sovranazionale

Nella storia della p. va fatta menzione dei piani internazionali, degli accordi cioè ricercati o stabiliti fra più paesi per coordinare il loro sviluppo economico. Merita innanzitutto di essere ricordato il Piano Marshall, che fu elaborato dagli USA nel 1948 in accordo con i paesi dell’OECE (Organizzazione Europea per la Cooperazione Economica) per provvedere alla loro ricostruzione dopo la Seconda guerra mondiale. Il Piano Colombo, dal nome della città nella quale fu presentato nel 1950, fu elaborato per promuovere lo sviluppo del Sud e del Sud-Est dell’Asia. Il Piano Schumann del 1950 fu la piattaforma per la creazione della CECA (Comunità Europea del Carbone e dell’Acciaio). Il Piano Mansholt del 1969 rappresentò, a livello comunitario, un importante momento del tentativo di coordinare alcuni aspetti della politica agricola dei paesi membri. Il Rapporto Delors, del 1989, definì un programma in tappe successive, per la realizzazione dell’unione economica e monetaria tra i paesi membri delle Comunità europee, servito di base per i negoziati sfociati nel Trattato di Maastricht del 1992, istitutivo dell’Unione Europea.

Istruzione

P. didattica L’attività di promozione, coordinamento, organizzazione e verifica dei diversi fattori educativi operanti all’interno di una unità scolastica (istituto, corso, classe). Implica una metodologia di lavoro collegiale riferita ai diversi elementi che interessano l’attività d’insegnamento-apprendimento (accertamento degli elementi cosiddetti di sfondo dell’ambiente scolastico, delle caratteristiche individuali e dei bisogni formativi degli alunni; definizione degli obiettivi didattici generali e specifici; selezione dei contenuti e determinazione delle sequenze di apprendimento; scelta di metodi, materiali e sussidi didattici; osservazione e verifica dei processi di apprendimento; valutazione complessiva del progetto adottato). Il primo provvedimento che fa riferimento esplicito alla p. è il d.p.r. 416/31 maggio 1974: l’art. 4 demanda al collegio dei docenti «la programmazione dell’azione educativa anche al fine di adeguare, nell’ambito degli ordinamenti della scuola stabiliti dallo Stato, i programmi d’insegnamento alle specifiche esigenze ambientali e di favorire il coordinamento interdisciplinare». Tale orientamento viene ripreso e reso più incisivo, sia pure limitatamente alla scuola dell’obbligo (elementare e media), dalla l. 517/4 agosto 1977. Viene stabilito, fra l’altro, che tra il 1° settembre e l’inizio delle lezioni il collegio dei docenti si riunisca per elaborare il piano annuale di attività, che costituisce la trama essenziale della p.; il collegio dei docenti procede periodicamente alla verifica e all’aggiornamento del piano, tenendo conto altresì delle indicazioni e degli adeguamenti suggeriti dai consigli di classe nelle loro verifiche periodiche dell’andamento didattico delle rispettive classi.

Matematica

P. matematica Branca della matematica applicata, e della ricerca operativa (➔ operativa, ricerca) in particolare, che studia i metodi per ottimizzare (cioè per determinarne i valori massimi o minimi) una particolare funzione, detta funzione obiettivo, in presenza di vincoli espressi da equazioni o disequazioni. A seconda della struttura dei vincoli e della funzione obiettivo i problemi di p. matematica prendono nomi particolari come, per es., p. lineare, p. non lineare, p. quadratica, p. a numeri interi, p. mista.

P. lineare

La p. lineare è caratterizzata da una funzione obiettivo lineare e da vincoli lineari (espressi mediante equazioni o disequazioni). È uno dei rami più importanti della ricerca operativa e trova larga applicazione in vari campi: in economia, in campo logistico-militare, nella produzione industriale: suoi problemi tipici sono, per es., l’impiego delle risorse aziendali in modo da minimizzare i costi o massimizzare i profitti, la distribuzione ottima della produzione nel tempo, la determinazione della dieta che soddisfa determinati requisiti alimentari.

Si dimostra che ogni problema di p. lineare può essere così rappresentato: data la funzione lineare, detta funzione obiettivo,

dove x₁, x₂, …, x_n sono le variabili e c₁, c₂, …, c_n sono costanti date, si tratta di renderla minima, le variabili x₁, x₂, …, x_n essendo soggette alle condizioni, o vincoli, (con m<n)

Si suppone che le equazioni siano linearmente indipendenti e, inoltre, che le condizioni [1] e [2] siano compatibili. In forma matriciale il problema può essere posto nella forma:

I problemi di p. lineare non possono essere risolti con il metodo dei moltiplicatori di Lagrange (di solito usato per la ricerca dei massimi e minimi vincolati) data appunto la linearità dei vincoli e della funzione da rendere minima. Qualunque sistema di valori delle variabili x_j che soddisfa le condizioni [1] è detto soluzione. Una soluzione che soddisfa anche le condizioni [2] si dice soluzione accettabile. Ogni insieme di m variabili x_j linearmente indipendenti, cioè tali che il determinante dei loro coefficienti a_ij nelle equazioni [1] non sia nullo, si chiama base. Le variabili che formano una base data si dicono variabili-base; le altre sono chiamate variabili non di base, o indipendenti. Data una base, la soluzione che si ottiene ponendo uguali a 0 le variabili non di base e risolvendo le equazioni [1] rispetto alle variabili-base è detta soluzione-base, e se è accettabile si chiama soluzione-base accettabile.

Si può ora enunciare il seguente teorema fondamentale: «se per un dato problema di p. lineare esiste una sola soluzione accettabile ottima (che, cioè, rende minima la funzione C), questa è una soluzione-base; se ve ne sono più di una, ve ne sono infinite, fra cui almeno due soluzioni-base». L’importanza del teorema consiste nel fatto che per trovare il minimo della funzione C non è necessario prendere in considerazione tutte le soluzioni, il cui numero in generale è infinito, del sistema costituito dalle condizioni [1] e [2]; basta limitarsi alle soluzioni-base accettabili, il cui numero non può essere maggiore di (nm). Per di più, tutte le soluzioni accettabili ottime, se ve ne è una pluralità, possono essere rappresentate come combinazioni lineari, con coefficienti non negativi, delle soluzioni-base ottime, purché (come generalmente avviene) le condizioni [1] e [2] siano tali da non ammettere valori infiniti delle variabili x_j. In questo caso è quindi sufficiente conoscere tali soluzioni-base per ottenere tutte le soluzioni accettabili ottime.

Il teorema sopra riportato trova il suo complemento, ai fini dell’elaborazione di un algoritmo per la soluzione dei problemi di p. lineare, nel cosiddetto criterio del simplesso, sul quale si fonda il metodo omonimo, dovuto a G.B. Dantzig. Tale criterio permette di stabilire se una data soluzione-base è ottima e, in caso contrario, indica il modo di giungere a una soluzione-base migliore. Con la terminologia precedente esso può essere così enunciato: «Espresse le variabili-base in funzione delle variabili indipendenti e sostituite le espressioni così ricavate nella funzione C, la soluzione-base data è ottima se le variabili indipendenti figurano tutte nella funzione C, così trasformata, con coefficienti non negativi. Se invece una delle variabili indipendenti ha coefficiente negativo, si ottiene una soluzione-base migliore introducendola nella base, cioè facendole assumere un valore positivo». Indicando con x_k1, x_k2, …, x_km, le variabili-base di una soluzione-base accettabile e con x_km+1, x_km+2, …, x_kn, le variabili indipendenti, si abbia, operate le sostituzioni: C=b₀₀+b_0km+1x_km+1+b_0km+2x_km+2+…+b_0knx_kn, dove b₀₀b_0km+1b_0km+2,…b_0kn sono delle costanti; se nessuno dei coefficienti b_0km+j (j = 1, 2, …, n−m) è negativo, b₀₀ è il valore minimo che la funzione C può assumere e la soluzione-base data è ottima, e precisamente è l’unica soluzione accettabile ottima se tutti i coefficienti b_0km+j sono positivi. Se uno o alcuni di detti coefficienti sono nulli, vi sono altre soluzioni-base accettabili ottime che si ottengono introducendo nella base le variabili corrispondenti. Se invece uno dei coefficienti, per es. b_0km+r, è negativo, si ottiene una soluzione-base migliore rimpiazzando con x_km+r una delle variabili-base. Tenendo presente quanto precede, il metodo del simplesso può essere così schematizzato. Si inizia con una soluzione-base accettabile e si verifica se essa è ottima. Se non lo è, si modifica la base, sostituendo una delle vecchie variabili-base con una variabile avente nella funzione C, trasformata nel modo sopra accennato, coefficiente negativo. Si prosegue così, fino a quando si verifica una delle seguenti alternative: a) si giunge a una soluzione-base ottima; b) oppure risulta che la funzione C non ha un minimo finito, in quanto una variabile con coefficiente negativo può assumere valori comunque grandi.

Il metodo del simplesso, pur rimanendo il più efficiente, almeno per quanto riguarda i problemi di piccole dimensioni, è stato posto in discussione e nuovi algoritmi sono stati proposti o sono in via di elaborazione. Dal punto di vista pratico, un filone di ricerca è quello legato allo studio di tecniche di implementazione numerica di algoritmi già formulati.

P. non lineare

La p. non-lineare si distingue dalla p. lineare in quanto o la funzione-obiettivo o alcuni o tutti i vincoli non sono lineari. Questi problemi presentano ovviamente difficoltà molto maggiori, dovute essenzialmente al fatto che i punti di massimo e di minimo non appartengono necessariamente alla frontiera dell’insieme definito dai vincoli. Un’altra complicazione è costituita dall’esistenza di punti di ottimo relativo.

I risultati più importanti conseguiti finora nella teoria della p. non lineare si riassumono nelle condizioni di Kuhn-Tucker per la individuazione dei punti di ottimo relativo. Si tratta di condizioni necessarie ma, in generale, non sufficienti, che possono essere enunciate come segue. Date le m+1 funzioni reali f(x₁, x₂, …, x_n), g₁(x₁, x₂, …, x_n), …, g_m(x₁, x₂, …, x_n), supposte dotate di derivate parziali continue, i punti P(x₁, x₂, …, x_n) di minimo relativo della funzione f(x₁, x₂, …, x_n) nell’insieme R_g definito dalle condizioni: g₁(x₁, …, x_n)≥0, …, g_m(x₁, …, x_n)≥0, x₁≥0, …, x_n≥0, devono verificare, insieme con le quantità l₁, …, l_m (moltiplicatori di Lagrange) le relazioni:

Le condizioni di Kuhn-Tucker sono sufficienti quando la f è funzione convessa, ossia il suo diagramma nello spazio a n+1 dimensioni è convesso rispetto all’asse della (n+1)-esima coordinata, e le g_i sono funzioni concave, come avviene in particolare nel caso della p. quadratica, in cui la f è costituita dalla somma di una forma quadratica semi-definita positiva e di una forma lineare, e i vincoli g_i sono lineari. È questo uno dei pochi casi di p. non lineare effettivamente risolubili.

Recentemente si sono registrati notevoli progressi, sia nel campo metodologico sia in quello computazionale e in particolare nella p. quadratica sono stati ottenuti importanti risultati. Oltre all’uso dei moltiplicatori di Lagrange, si ricorre sempre più spesso a quello di insiemi fiduciari, ottenuti aggiungendo un vincolo che definisce una regione fiduciaria entro la quale l’approssimazione operata è sufficientemente buona.

P. a numeri interi

La p. a numeri interi è caratterizzata dal fatto che le variabili sono vincolate ad assumere solo valori interi. In questo caso i problemi possono essere generalmente ricondotti al caso, detto di p. lineare a numeri interi, in cui tutti i vincoli, con l’eccezione di quelli di interezza, sono lineari. Questi problemi sono normalmente di difficile soluzione. Vi è in letteratura un’ampia gamma di tecniche risolutive esatte o approssimate, spesso rivolte a particolari classi di problemi. I principali algoritmi di soluzione appartengono alle seguenti classi: algoritmi enumerativi, in cui vengono enumerate possibili soluzioni in numero il più possibile limitato, fino ad arrivare alla certezza di aver trovato quella ottima o una che garantisca una assegnata approssimazione; algoritmi poliedrali, in cui vengono introdotti vincoli aggiuntivi fino a che i vertici del problema di p. lineare che si ottiene eliminando i vincoli di interezza non sono interi: a questo punto i metodi di soluzione della p. lineare trovano l’ottimo; algoritmi euristici, che non danno garanzie di approssimazione: ve ne sono di diverso tipo, generalmente basati sulla generazione di una sequenza di soluzioni ammissibili sempre migliori, fino a quando una assegnata regola di arresto non ferma la procedura. Le tecniche utilizzate per la p. a numeri interi sono generalmente estendibili al caso in cui solo parte delle variabili sono vincolate all’interezza (p. mista).

P. dinamica

Non si tratta tanto di una classe definita di problemi, quanto di un diverso approccio per la soluzione dei problemi, lineari o no, di ottimizzazione vincolata. La tecnica della p. dinamica si fonda sul principio di ottimalità, che in termini di teoria delle decisioni può essere così enunciato: «Una scelta ottimale possiede la proprietà che, quali che siano lo stato e la decisione iniziali, le decisioni rimanenti costituiscono una scelta ottimale nei riguardi dello stato che risulta dalla prima decisione». L’applicazione di detto principio comporta che le variabili siano prese una alla volta mediante formule ricorrenti che dipendono dalla natura del problema da trattare e permettono di passare da un problema a i variabili al corrispondente problema a i+1 variabili. In particolare, dette x₀, x₁, …, x_n, n variabili di stato e a₀, a₁, …, a_n una sequenza di azioni tali che la conoscenza dello stadio (x_i, a_i) permetta la conoscenza dello stato x_i+1; indicando con w(x_i, a_i) il costo nel passaggio da uno stadio al successivo e con J_i il costo rimanente per passare dallo stato x_i a quello finale x_n si ha l’equazione di R. Bellman:

minJ_i=min_ai[w(x_i, a_i)+minJ_i+1], minJ_n=0,

che, risolta, permette di determinare le sequenze delle azioni migliori.