cissoide

fig. 1

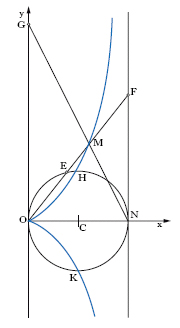
Curva piana, detta anche, dal nome dello scopritore, c. di Diocle (fig. 1). Dati una circonferenza di centro C e un suo diametro ON, si consideri la tangente in N, e su ogni retta per O che intersechi la circonferenza in E e la tangente in F, si porti, a partire da O, il segmento OM=EF: la c. è il luogo dei punti M. Se si scelgono gli assi cartesiani x, y come in fig. e si pone ON=1, la c. ha equazione:

x(x²+y²)−y²=0.

La c. è una cubica razionale, con una cuspide nell’origine O; si protende all’infinito e ha per asintoto la tangente alla circonferenza in N. I Greci (in particolare Diocle) consideravano solo il tratto finito HOK (e allora la figura limitata da questo tratto della c. e dalla semicirconferenza HNK ricorda una foglia d’edera).

Problema della duplicazione del cubo Posto NF=m ON, si ricava: OG=m³ ON, così che, viceversa, basta prendere OG=2 ON perché risulti

NF=³√‾‾2 ON.

In questo modo, supposta tracciata la c., è immediata la soluzione del problema della duplicazione del cubo (o problema di Delo della geometria antica, risolto da Diocle al principio del 2° sec. a.C.): «determinare lo spigolo NF del cubo di volume doppio di quello del cubo di spigolo ON».

fig. 2

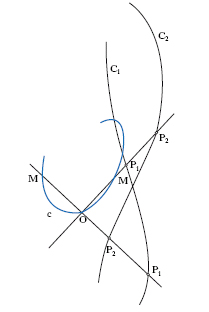
C. generalizzata (fig. 2) Date in un piano due curve C₁ e C₂, si conduca per un punto fisso O una qualsiasi retta a incontrare le due curve in P₁, P₂ e su di essa si prenda il punto M tale che OM=OP₂−OP₁: il luogo c di M si dice linea cissoidale o c. generalizzata.