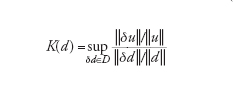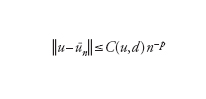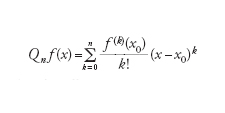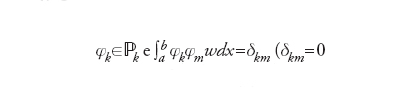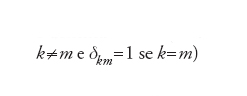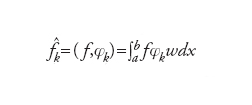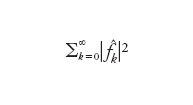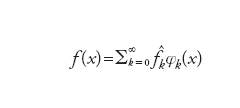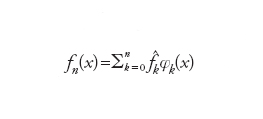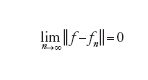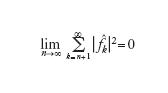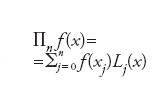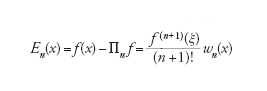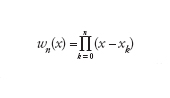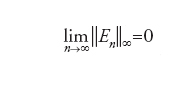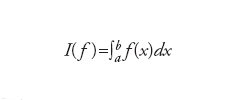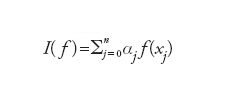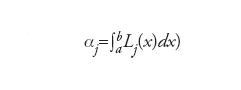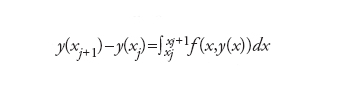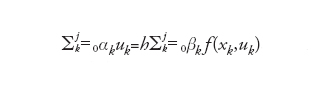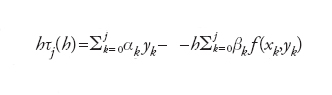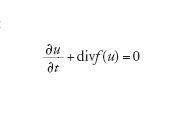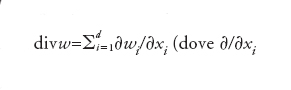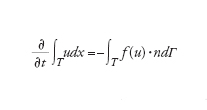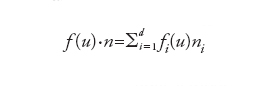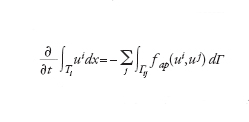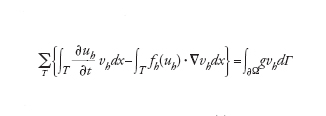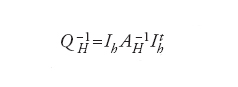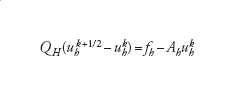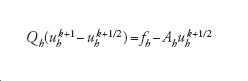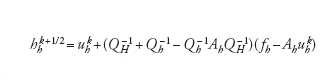Computazionali, metodi

Computazionali, metodi

I metodi computazionali permettono di risolvere con i computer, nell'ambito delle scienze applicate, problemi complessi formulabili tramite il linguaggio della matematica e raramente risolubili per via analitica. In generale, la loro soluzione non ammette una rappresentazione in forma esplicita: basti pensare a equazioni o sistemi non lineari (algebrici, differenziali o integrali), di cui non siano note formule risolutive. In altri casi la forma esplicita, pur nota, non è praticamente utilizzabile per determinare valori quantitativi della soluzione stessa, o perché essa richiederebbe una quantità proibitiva di operazioni, o perché espressa a sua volta attraverso altri enti matematici (quali integrali o sviluppi in serie), di cui sarebbe difficile dare una valutazione quantitativa. La risoluzione di problemi di interesse applicativo comporta diverse fasi: (a) la comprensione qualitativa e quantitativa del problema; (b) la sua modellazione attraverso equazioni matematiche che possono essere algebriche, funzionali, differenziali o integrali (modello matematico); (c) l'individuazione di metodi della matematica numerica che siano idonei ad approssimare tale modello matematico (discretizzazione); (d) l'implementazione di tali metodi numerici di approssimazione su calcolatori.

I metodi computazionali comprendono ed esauriscono le fasi (c) e (d) del processo. La scelta di tali metodi non può prescindere da una conoscenza adeguata delle proprietà qualitative della soluzione del modello matematico e da una buona percezione della fenomenologia del problema originario. È pertanto giustificata la terminologia di modelli computazionali che viene usata in alternativa a quella di metodi computazionali. La modellistica computazionale è un settore di ricerca interdisciplinare, che si trova alla confluenza della matematica, dell'informatica e delle scienze applicate. La sua evoluzione è stata molto rapida negli anni recenti, grazie al vigoroso sviluppo dei calcolatori e degli algoritmi, nonché a una maggior consapevolezza del ruolo che il calcolo scientifico può rivestire nella simulazione di complessi problemi di interesse scientifico/teorico, industriale, ambientale e sociale.

fig. 1

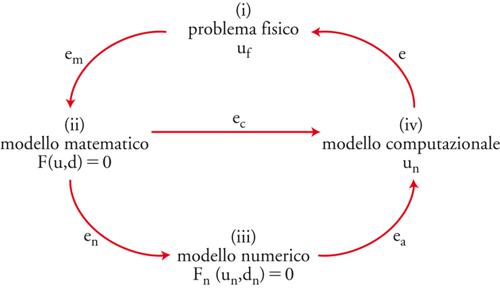
Si può riassumere in forma schematica il processo (a)-(d) con l'ausilio di un diagramma (fig. 1). Indichiamo con uf la soluzione del problema originario, qui detto per brevità problema fisico. Il modello matematico che descrive il problema fisico è posto nella forma F(u,d)=0, dove si suppone che d descriva l'insieme dei dati, u la soluzione, e F la relazione funzionale che lega fra loro dati e soluzione. Vari e diversificati sono i problemi matematici che, in astratto, possono essere formulati in questo modo. Si pensi all'integrazione definita di una funzione, alla ricerca delle radici di equazioni algebriche, alla soluzione di problemi differenziali (ordinari o alle derivate parziali).

Svariati altri modelli matematici sono oggetto d'interesse per la modellistica computazionale. Si pensi, per esempio, al problema della rappresentazione di curve e superfici, al trattamento numerico di immagini e segnali, alla minimizzazione di funzionali liberi o vincolati, alla regolarizzazione numerica e risoluzione di problemi inversi, ai problemi integro-differenziali, nonché al controllo di sistemi differenziali, integrali o di natura stocastica. La rilevanza di tali modelli nell'analisi e simulazione di processi meccanici, fisici, economici, biologici ecc. è notevole e destinata a crescere nel tempo.

Convergenza e stabilità dei modelli numerici

La prima fase della modellistica computazionale consiste nella sostituzione del modello matematico F(u,d)=0 con uno numerico F_n(u_n,d_n)=0, dipendente da un parametro n il cui significato varia a seconda della famiglia di problemi considerata, ma che possiamo sempre pensare riferito alla dimensione del modello numerico medesimo. In tale contesto, d_n è un'approssimazione di d, F_n una discretizzazione della relazione funzionale F e u_n la soluzione numerica. La proprietà fondamentale che si richiede a un modello numerico è la convergenza, ovvero che (in un'opportuna topologia) lim_n→∞u_n=u. Condizione necessaria perché ciò avvenga è che F_n traduca correttamente la legge funzionale F, ovvero che F_n(u,d)→0 per n→∞, essendo d un dato ammissibile per il modello matematico e u la corrispondente soluzione. Tale proprietà, detta consistenza, non è peraltro sufficiente a garantire la convergenza della soluzione numerica a quella esatta: a tale scopo serve che il modello numerico sia stabile. Al fine di definire cosa si intende con stabilità, ricordiamo che un modello matematico si dice ben posto se ammette una sola soluzione e se, a piccole perturbazioni dei dati, corrispondono variazioni controllabili della soluzione. In altri termini, se supponiamo che d e d* rappresentino due insiemi di dati, δd=d*−d la loro differenza, u e u* le soluzioni corrispondenti e δu=u*−u la loro differenza, allora il problema sarà ben posto in corrispondenza del dato d se per ogni ε>0 esiste K(ε,d) tale che se ∥δd∥〈ε allora ∥δu∥≤K(ε,d)∥δd∥. Abbiamo indicato con lo stesso simbolo ∥∙∥ delle norme opportune (non necessariamente le stesse) per l'insieme dei dati e per quello delle soluzioni. Se d≠0, il numero di condizionamento K(d) del modello è definito come:

[1] formula

dove l'estremo superiore viene preso sull'insieme D di tutte le perturbazioni (non nulle) ammissibili dei dati.

Il numero K esprime dunque il massimo valore possibile del rapporto fra l'errore relativo sulla soluzione e l'errore relativo sui dati. I problemi per i quali K è dell'ordine dell'unità si dicono ben condizionati, se invece K è molto grande si diranno mal condizionati. Supponiamo che la soluzione u del problema modello si possa rappresentare come u=f(d) e analogamente la soluzione del modello numerico si possa ottenere come u_n=f_n(d_n), essendo f e f_n due opportune leggi di corrispondenza. Allora, se f è differenziabile, l'uso del teorema del valor medio consente di ottenere per K(d) la seguente stima: K(d)=∥f′'(d)∥∙∥d∥/∥f(d)∥ (avendo trascurato infinitesimi di ordine superiore a ∥δd∥). Con ragionamenti del tutto analoghi possiamo associare al modello numerico un numero di condizionamento K_n(d_n)=∥f′_n(d_n)∥∙∥d_n∥/∥f_n(d_n)∥. Se l'insieme dei dati {d_n} coincide con {d}, possiamo definire K* (d)=lim_→∞sup_n≥K_n(d). Il numero K* viene detto numero di condizionamento asintotico del modello numerico.

Siamo ora in grado di precisare il concetto di stabilità numerica. Dato un modello matematico ben condizionato con numero di condizionamento K, diremo che la famiglia (dipendente dal parametro n) di modelli numerici associati è stabile se K* è dello stesso ordine di grandezza di K. In caso contrario, si parlerà di modello numerico instabile. Si noti che, in particolare, la stabilità assicura la limitatezza uniforme (rispetto a n) delle soluzioni numeriche. A titolo d'esempio, consideriamo il seguente modello matematico elementare: trovare x tale che x²−2px+1=0, dove p è il dato e le soluzioni sono le due radici x_±=F(p)=p±√(p²−1). Per p>1, il numero di condizionamento corrispondente è K=∣p∣/√(p²−1). Esso degenera per p→1 in quanto le due radici sono coincidenti per p=1; tuttavia, anche per p=1 il problema della ricerca delle radici è ben posto, come si vede trasformandolo nel problema equivalente F(x,t)=x²−[(1+t²)/t]x+1=0, con t=p+√(p²−1), le cui radici x₋=t e x₊=1/t risultano coincidenti per t=1.

Il cambio di parametro rimuove la singolarità presente nella precedente rappresentazione delle radici in funzione di p e il calcolo del condizionamento restituisce K≃1 per ogni valore di t. Supponendo p≫1 in modo che le radici siano ben separate, il problema è ben condizionato, ma il calcolo di x₋ attraverso la formula esplicita è instabile per via della cancellazione di cifre significative, tipica dell'aritmetica finita del calcolatore. Se si usa invece il processo iterativo di Newton (adottato da quasi tutte le calcolatrici tascabili per il calcolo delle radici quadrate), ovvero x_n=x_n−(x²⁻¹_n−2px_n+1)/(2x_n−2p)≡≡f_n(p), n≥1, si ottiene K_n=∣p∣/∣x_n−p∣. Se x₀ è scelto opportunamente allora x_n, per n→∞, converge a una delle radici e si vede che K*=∣p∣/∣x_±−p∣=K. Si tratta dunque di un modello numerico stabile. Questo elementare esempio evidenzia come problemi ben condizionati possano essere affrontati con metodi numerici stabili o instabili.

Errore computazionale e modelli adattivi

Il modello matematico mira a legare fra loro quantità di interesse fisico attraverso relazioni matematiche, spesso semplificate rispetto alla complessità del problema originario (per le nostre notazioni faremo costante riferimento al diagramma riportato nella fig. 1). La soluzione u del modello matematico sarà di conseguenza diversa da quella u_f del problema fisico in esame, e tale differenza e_m=u_f−u renderà conto sia della significatività (e ragionevolezza) delle ipotesi semplificative adottate, sia dell'accuratezza con la quale le quantità fisiche reali sono state rappresentate dall'insieme dei dati del modello. L'errore e_m è pertanto intrinseco al processo. Il modello computazionale creerà un altro errore, indicato con e_c, che esprime la distanza fra la soluzione effettivamente calcolata ū_n e u. L'errore globale e, differenza fra la reale soluzione fisica u_f e quella calcolata ū_n, risulterà dalla sovrapposizione dei due errori e_m e e_c.

L'obiettivo della modellistica computazionale è di garantire che l'errore e_c sia piccolo e controllabile (affidabilità) con il minor costo computazionale possibile (efficienza). Per costo computazionale si intende la quantità di risorse (tempo di calcolo, occupazione di memoria) necessaria per calcolare la soluzione ū_n. L'affidabilità è un requisito cruciale di un modello computazionale: l'analisi mira a trovare stime dell'errore e_c (in funzione dei dati del problema e dei parametri della discretizzazione) che consentano di garantire che esso stia al di sotto di una certa soglia di precisione fissata a priori. A questo scopo, è utile ricorrere ad algoritmi adattivi che adottano una procedura di retroazione (o feedback) a partire dai risultati già ottenuti per modificare i parametri della discretizzazione e migliorare la qualità della soluzione. I metodi numerici che implementano una strategia adattiva per il controllo dell'errore sono detti modelli computazionali adattivi.

Vediamo come viene generato l'errore computazionale. Il modello numerico deve essere implementato su calcolatore con l'ausilio di un algoritmo opportuno. Si generano di conseguenza nuovi errori, alcuni intrinseci all'algoritmo, altri attribuibili all'aritmetica finita di cui fa uso ogni calcolatore per rappresentare i numeri reali ed eseguire operazioni algebriche elementari. Per esempio, se il modello matematico è rappresentato dal problema differenziale u′=G(u) e per la discretizzazione della derivata si usano rapporti incrementali all'indietro, si ottiene come modello numerico un sistema di equazioni algebriche (lineari o non, a seconda della linearità o meno di G rispetto all'incognita u). Nel caso lineare possiamo rappresentare il sistema nella forma generale Ax=b, con A una matrice n×n, b un termine noto, x un vettore incognito (avendo indicato con n l'insieme dei nodi in cui si cerca la soluzione numerica). Anche nel caso di problemi differenziali non lineari, si perviene a un sistema lineare (previa opportuna linearizzazione) utilizzando tecniche à la Newton; si ottengono sistemi lineari in innumerevoli altre circostanze, in particolare nell'approssimazione numerica di problemi differenziali alle derivate parziali.

Nell'ipotesi in cui A sia non singolare, la soluzione del sistema lineare x=A⁻¹ è nota in forma esplicita attraverso la formula di Cramer, che peraltro richiede un numero di operazioni elementari superiore a n!. Tale numero è proibitivo anche se n non è troppo grande (nelle applicazioni ai problemi differenziali, n tipicamente è dell'ordine di 10^p per 2≤p≤6), anche per calcolatori, come gli attuali, in grado di effettuare diverse centinaia di miliardi di operazioni al secondo. Algoritmi numerici efficienti, quali l'algoritmo di fattorizzazione di Gauss, o algoritmi iterativi in sottospazi di Krylov, multigriglia o multilivello, consentono di ridurre il costo sino alla soglia ottimale N≃n, introducendo tuttavia un ulteriore errore. La combinazione di tale errore con gli errori di arrotondamento dell'aritmetica finita (quest'ultimo decresce esponenzialmente con −t, dove t è il numero di cifre significative della macchina) fornisce l'errore algoritmico e_a=u_n−ū_n. L'errore del modello computazionale (e_c=u−ū_n) è la somma dell'errore numerico (e_n=u−u_n) e di quello algoritmico.

L'obiettivo ultimo dell'analisi dell'errore ec del modello computazionale è quello di dimostrare che esso tende a zero per n→∞. Più precisamente, si cercano stime del tipo

[2] formula

per un'opportuna norma ∣∣∙∣∣ che dipenderà dal problema in esame. L'esponente p (ordine di infinitesimo dell'errore rispetto a 1/n) è l'ordine del modello numerico. Nell'ipotesi ottimale in cui l'errore algoritmico ea sia controllabile con la tolleranza desiderata, p è lo stesso ordine di infinitesimo con cui en tende a zero rispetto a 1/n. La tecnica dimostrativa che consente di ottenere stime dell'errore del tipo indicato è basata sull'analisi di 'buona posizione' del modello matematico e su quella di stabilità del modello numerico. Essa è detta analisi a priori, in quanto può operarsi prima di implementare effettivamente il modello numerico e dipende in maniera implicita dal numero di condizionamento matematico K e da quello numerico K*. La costante C(u,d) dipende dai dati del problema, nonché da u e dalle sue derivate (supposto che esistano) fino a un ordine opportuno, legato al valore di p. La sua quantificazione numerica è generalmente assai difficile. Di conseguenza, la stima sopra riportata è incompleta: consente di prevedere la tendenza di decadimento dell'errore per n crescenti, ma non di fornirne una quantificazione numerica accurata per n fissato.

È compito dell'analisi a posteriori completare questa lacuna. Essa, sulla base della soluzione ūn effettivamente calcolata in corrispondenza di un certo valore del parametro di discretizzazione n e del valore del residuo r_n=F(ū_n,d) (una misura indiretta dello scostamento di ū_n da u), consente di stabilire se l'errore sia o meno al di sotto di una prestabilita tolleranza. Se ciò non è vero, un algoritmo adattivo indica come migliorare la discretizzazione (fornendo un criterio per la modifica di ū_n) al fine di garantire una riduzione dell'errore. Nel caso elementare di un sistema lineare, se x−indica una soluzione calcolata (con un qualunque algoritmo numerico) e r=b−Ax− è il residuo a essa associato, si può facilmente verificare che ∥x−x−∥/∥x∥≤K(A)∥r∥/∥b∥, dove ∥∙∥ indica la norma euclidea e K(A) è il numero di condizionamento della matrice (se A è una matrice simmetrica con autovalori reali positivi K(A)=λ_max/λ_min, dove λ_max e λ_min sono rispettivamente il massimo e il minimo autovalore di A); dunque l'errore computazionale (relativo, o percentuale) è maggiorabile con il residuo (relativo) a meno del fattore K(A) che, in questo contesto, viene detto fattore di stabilità. Per problemi più complessi lo spirito è il medesimo, pur essendo in generale più difficile determinare i fattori di stabilità. I modelli computazionali adattivi combinano pertanto l'analisi a priori con quella a posteriori al fine di ottenere stime quantitativamente accurate dell'errore computazionale.

I metodi numerici

Intrinseco al concetto di modello computazionale è quello di metodo numerico per la realizzazione della fase (c) del processo che stiamo esaminando (fig. 1). Le componenti essenziali di un metodo numerico si possono classificare in rapporto al loro scopo, che può essere quello di: (1) rappresentare in modo approssimato una funzione (o una successione finita di dati sperimentali); (2) approssimare il valore numerico di un integrale; (3) approssimare (localmente o globalmente) derivate di ordine arbitrario; (4) approssimare soluzioni di relazioni funzionali (lineari e non) attraverso successioni il cui termine generale sia facile da ottenere e la cui velocità di convergenza sia la più elevata possibile; (5) decomporre matrici di struttura generale nel prodotto di matrici più semplici, per esempio triangolari, allo scopo di facilitare la risoluzione di sistemi lineari di grandi dimensioni.

Approssimazione di funzioni

Se f:[a,b]→ℝ è una funzione reale nota, definita sull'intervallo [a,b] della retta reale, ci si pone spesso il problema di darne una rappresentazione approssimata, per esempio tramite un polinomio o un polinomio a tratti, ovvero una funzione continua che sia un polinomio su ogni sottointervallo [a_k,b_k] di una certa partizione di [a,b]. Le ragioni per le quali si cercano approssimanti polinomiali sono molteplici. Innanzitutto, i polinomi sono semplici da trattare: è immediato derivarli e integrarli, ed è facile, grazie all'algoritmo di Horner, valutarli in punti prestabiliti. È inoltre noto dal teorema di Weierstrass che ogni funzione continua può approssimarsi con ordine arbitrario di accuratezza con un polinomio di grado opportuno. Precisamente, per ogni f∈C([a,b]) e ε>0 esistono n=n(ε) e p_n∈ℙ_n tale che ∥f−p_n∥_∞〈ε, ove qui e nel seguito si indica con ∥g∥_∞ il massimo valore di ∣g(x)∣ nell'intervallo [a,b], g essendo una generica funzione continua. Abbiamo denotato con ℙ_n l'insieme dei polinomi algebrici di grado inferiore o uguale a n.

Il teorema di Weierstrass, tuttavia, non è costruttivo: esso non permette di conoscere n(ε), né di costruire praticamente p_n. Esempi di risultati costruttivi sono invece forniti sia dal teorema di Taylor sia dalla teoria dei polinomi ortogonali. Il primo assicura che se f∈Cⁿ([a,b]), il polinomio

[3] formula

di grado n è un'eccellente approssimazione di f e delle sue derivate in un intorno del punto x₀∈(a,b), ma sfortunatamente l'accuratezza diminuisce se x si allontana da x₀. Si parla in tal caso di approssimazione locale.

Esempi di approssimazione globale sono forniti dalle serie troncate di sviluppi di f rispetto a basi di polinomi ortogonali. La famiglia {φ_k, k=0,1,…} di polinomi ortogonali in [a,b] rispetto alla funzione peso w(x)>0 è definita come segue:

se

Se a=−1 e b=1, per w(x)=1 si ottengono i polinomi di Legendre e per w(x)=1/√(1−x²) si ottengono quelli di Cebycev. Su un intervallo arbitrario tali definizioni si estendono in modo ovvio. Ora,

è il coefficiente k-esimo di Fourier (generalizzato) di f; se la serie

converge, allora si ha

Indicando dunque con ∥f∥ = =(f,f)^1/2 la cosiddetta norma L² di f in (a,b) e, per ogni n, con

la serie troncata di f (si noti che f_n∈ℙ_n), abbiamo

[4] formula

o, equivalentemente,

[5] formula.

La convergenza è tanto più rapida quanto più f è regolare, per n→∞ si ha che ∣f^‸_n∣ tende a zero come (1/n)p se f∈Cp([a,b]) per un certo p≥1. Tuttavia, la costruzione dei coefficienti {f^‸_n, k=0,…,n} è assai problematica e deve essere fatta in modo approssimato ricorrendo a formule di integrazione numerica gaussiane, in modo da preservare l'ordine di convergenza della serie.

Un approccio più semplice consiste nel sostituire f con un polinomio ∏_nf di grado n che interpoli f in n+1 nodi distinti x₀,…,x_n di [a,b], ovvero ∏_nf(x_j)=f(x_j) dove j=0,…,n. Tale polinomio si può rappresentare come

essendo l'unico polinomio di grado n tale che L_j(x_i)=δ_ij. L'errore che si genera è

[6] formula

essendo ξ un punto opportuno di [a,b] e

[7] formula

il cosiddetto polinomio nodale. Se i nodi sono equispaziati, si possono fornire esempi di funzioni per le quali la proprietà di convergenza uniforme

non è verificata. A tal fine è possibile ricorrere a nodi opportunamente distribuiti, detti di tipo gaussiano: si considerano gli zeri del polinomio ortogonale φ_n+1 oppure le radici del polinomio (x−a)(x−b)φ′_n(x). Con tali scelte si ottiene, oltre alla convergenza uniforme, una stima dell'errore del tipo ∥E_n∥_∞≤Cn−p, nell'ipotesi che f∈Cp([a,b]) (qui e nel seguito, C denota una costante positiva indipendente da n). Un'altra strategia conduce alla cosiddetta interpolazione composita: si suddivide dapprima [a,b] in sottointervalli disgiunti, di ampiezza h, e in ognuno si approssima f con una funzione continua ∏_hf,r la cui restrizione su ogni intervallo è un polinomio interpolatore di grado basso, per esempio r=1,2. In tal caso l'errore E_hr generato verifica una disuguaglianza del tipo ∥E_hr ^(k)∥≤Ch^r+1−k con k=0,1, avendo supposto f sufficientemente regolare, per esempio f∈C^r+1([a,b]). L'idea dell'interpolazione composita si estende senza difficoltà al caso multidimensionale ed è alla base del processo di discretizzazione degli elementi finiti, nonché dell'approssimazione con funzioni spline, nel qual caso si cercano raccordi anche per la derivata prima agli estremi dell'intervallo di integrazione.

Approssimazione di integrali

Per l'approssimazione del valore

un'idea naturale è quella di calcolare I(f_n), dove f_n è un'approssimazione polinomiale di f. Prendendo per esempio f_n=∏_nf, si otterrà

(dove formula),

ovvero una formula di integrazione numerica in cui i punti {x_j} sono ancora detti nodi, mentre i coefficienti {α_j} sono detti pesi. Nel caso di interpolazione con nodi equispaziati, si ottengono le cosiddette formule di Newton-Cotes. Otterremo invece formule di integrazione gaussiana (assai più precise nell'integrazione di funzioni polinomiali) nel caso in cui si usino nodi di interpolazione gaussiana. La valutazione dell'errore di integrazione I(f)−I(f_n) viene ereditata dalla stima del corrispondente errore E_n. Una naturale evoluzione in questa direzione si basa sull'uso di polinomi di interpolazione composita ∏_hf,r, nel qual caso l'integrale su [a,b] verrà approssimato da una somma di integrali approssimati su ogni sottointervallo.

Un approccio diverso dai precedenti è alla base dei metodi di tipo Monte Carlo, dove i nodi sono scelti in modo statistico in funzione dei valori assunti da variabili casuali aventi una distribuzione di probabilità nota. Nella pratica computazionale i nodi sono ottenuti tramite un generatore di numeri casuali, e le formule che ne derivano si dicono di integrazione numerica pseudo-casuali. L'errore di integrazione su regioni dello spazio ℝⁿ decresce come 1/√N (N essendo il numero di nodi), indipendentemente dalla dimensione n.

Approssimazione delle derivate di una funzione

Per approssimare in opportuni nodi i valori della derivata di una funzione f, una via naturale è ricorrere alla definizione stessa di derivata e sostituire f′(x_k) con opportuni rapporti incrementali nei nodi adiacenti. Nel caso di nodi equispaziati, indicando con h la distanza fra due nodi consecutivi e con f_k il valore f(x_k), si può approssimare f′(x_k) con (f_k+1−f_k−1)/h (ma anche con (f_k−f_k−1)/h) a meno di infinitesimi di ordine superiore a h. Un'accuratezza di ordine superiore si ottiene con il rapporto incrementale centrato (f_k+1−f_k−1)/2h, come si vede applicando la formula di Taylor. Naturalmente, iterando i precedenti rapporti incrementali si ottengono formule di approssimazione per derivate di ordine superiore. Questo processo, di tipo locale, è alla base dell'approssimazione alle differenze finite di problemi di Cauchy. Un approccio globale si ottiene invece approssimando f′(x) su un intero intervallo (a,b) con la derivata esatta di un polinomio approssimante f in (a,b), ottenuto tramite uno dei metodi precedentemente illustrati. Utilizzando per esempio il polinomio ∏_nf interpolante f in n+1 nodi di tipo gaussiano, si ottiene dall'analisi precedente che ∥f′−(∏_nf)′∥_∞≤Cn^−(p−1), avendo ancora assunto f∈C^p([a,b]). Questo processo è alla base dell'approssimazione di problemi ai limiti con metodi spettrali.

Iterazioni funzionali

Capita assai di frequente di dover trovare per via approssimata la soluzione di equazioni funzionali della forma F(x)=0, dove F è un sistema di equazioni, lineari o non. Una metodologia generale assai naturale consiste nel realizzare un processo iterativo della seguente forma: assegnato x₀, per ogni k≥0 si ottiene x_{k +1}

da x_k risolvendo il problema G^k(x_k+1−x_k)=−F(x_k), dove G^k è un'approssimazione opportuna della matrice jacobiana F′ ( x_k) di F nel punto x_k. Chiameremo la matrice G^k operatore di precondizionamento e la supporremo invertibile con inversa H^k. Nel caso in cui F sia una trasformazione affine F(x)=Ax−b, la matrice G^k costituirà un'opportuna approssimazione della matrice A, e il processo iterativo ricomprenderà i classici metodi iterativi dell'algebra lineare numerica (di Jacobi, di Gauss-Seidel, di Richardson, del gradiente, e così via). Indicato con e_k=x−x_k l'errore all'iterazione k-esima e con I la matrice identità, si ha e_{k +1}=(I−H^kA)e_k e per la convergenza del processo iterativo si richiederà che ϱ_k=ϱ(I−H^kA) sia minore di 1 (ϱ_k è il raggio spettrale della matrice I−H^kA). Nel caso in cui F(x)=0 sia un'equazione (o un sistema di equazioni) non lineare, il processo descritto è il paradigma di numerosi metodi classici, quali il metodo delle corde, di Newton e del gradiente.

L'analisi dell'errore si può fare analogamente al caso lineare. Supponendo infatti F differenziabile in un intorno della soluzione, si avrà e_k+1=(I−H^kF′ (y_k))e_k, dove y_k è compreso fra x e x_k. Il processo iterativo precedente comporta a ogni iterazione la risoluzione di un sistema lineare nella matrice G^k. Per la sua efficienza si richiede un compromesso fra la semplicità computazionale e la velocità di convergenza: infatti, G^k dovrebbe essere al tempo stesso di forma semplice (diagonale, triangolare, a banda, ecc.) e tale che lo spettro di H^kF′(y_k) sia il più compatto possibile, in modo da garantire che ϱ_k (o un'opportuna norma di I−H^kF′(y_k) nel caso non lineare), sia più piccolo di 1 e più vicino possibile a 0.

Decomposizione di matrici

Per una matrice quadrata A non singolare di n righe si possono in generale trovare due fattori: una matrice L triangolare inferiore (ovvero con elementi nulli al di sopra della diagonale principale) e una U triangolare superiore (con elementi nulli al di sotto della diagonale principale), tali che A=LU. Questa decomposizione (che esiste a meno di possibili permutazioni di righe o colonne di A) è unica se, per esempio, si fissano uguali a 1 gli elementi diagonali di L (ottenendo in tal modo la cosiddetta decomposizione di Gauss) o quelli di U (decomposizione di Crout). Note le matrici L e U, la risoluzione di un sistema Ax=b può ricondursi a quella di due sistemi triangolari Ly=b e Ux=y (in sequenza); ognuno di essi può essere risolto con il metodo delle sostituzioni in avanti per L, all'indietro per U, con un costo computazionale di n² operazioni. Nel caso in cui A sia simmetrica con autovalori positivi, essa ammette la decomposizione (detta di Cholesky) A=HH^t, dove H è triangolare inferiore e H^t ne è la trasposta, che naturalmente risulta triangolare superiore.

Conviene inoltre citare la cosiddetta decomposizione QR per la risoluzione di sistemi lineari sovradeterminati Ax=b, dove b è un vettore di m componenti, x un vettore di n componenti e A una matrice di m righe ed n colonne, con m>n. Non esistendo una soluzione in senso classico, se ne può cercare una x*, detta soluzione nel senso dei minimi quadrati, risolvendo il sistema n×n: A^t(Ax*−b)=0. Il classico problema della determinazione della retta di regressione lineare, che minimizza la somma dei quadrati delle distanze da una distribuzione di osservate {b_i,i=1,…,m}, si formula esattamente in questo modo (in questo caso n=2 è il numero di coefficienti in grado di individuare la retta di regressione). Siano Q,R due matrici rispettivamente m×n ed n×n, l'una ortogonale e l'altra triangolare superiore, per le quali si abbia A=QR. Indicata con D la matrice diagonale Q^tQ, il sistema trasformato si può riscrivere nel modo seguente: R^tQ^t(QRx*−b)=0, ovvero R^t(DRx*−Q^tb)=0. Si è dunque condotti alla risoluzione in sequenza di due sistemi di struttura elementare: uno diagonale, Dy=Q^tb, l'altro triangolare, Rx*=y.

Modellistica computazionale per problemi differenziali

La complessità dei problemi differenziali, ordinari e alle derivate parziali, e la loro rilevanza nella modellistica fisico-matematica hanno stimolato negli ultimi decenni un enorme sviluppo di metodi numerici e computazionali adatti alla loro risoluzione.

Equazioni differenziali ordinarie

Consideriamo l'equazione differenziale ordinaria al prim'ordine y′(x)=f (x,y (x)), per x≥x₀, con un dato iniziale y(x₀)=y₀. Supporremo f lipschitziana rispetto all'argomento y in un intorno di (x₀,y₀), ovvero che esista una costante L>0 tale che ∣f(x,y₁)−f(x,y₂)∣≤L∣y₁−y₂∣ per ogni y₁,y₂. Ciò assicura che esiste una soluzione del problema, quantomeno in un intorno I=[x₀,b] del punto iniziale x₀. Consideriamone un'approssimazione basata sul metodo delle differenze finite. Passo preliminare è la suddivisione di I in n sottointervalli di ampiezza h, i cui estremi x_j=x₀+jh, con j=0,…,n, sono detti nodi. Il modello numerico genererà dei valori {u_j} approssimanti la soluzione esatta y nei nodi {x_j}. Una famiglia di metodi numerici è basata sull'idea di soddisfare l'equazione differenziale solo nei nodi, dopo aver sostituito la derivata prima con una sua conveniente approssimazione che faccia uso dei valori nodali. Come approssimante si può scegliere sia un rapporto incrementale sia la derivata prima del polinomio interpolatore (in quest'ultimo caso i nodi dovranno essere non più equispaziati, ma di tipo gaussiano e h denoterà la massima distanza fra due nodi consecutivi). Un'altra strategia si basa sull'uso della formula fondamentale del calcolo integrale

,

dove l'integrale stesso è sostituito con un'opportuna formula interpolatoria in alcuni dei nodi {x₀,x₁,…,x_{j +1}}.

Astrattamente, in entrambi i casi il problema numerico assumerà la forma seguente:

,

dove i coefficienti {α_k} e {β_k} (non tutti necessariamente diversi da zero) caratterizzano lo schema. Possiamo ora esaminare il significato dei concetti generali di convergenza, consistenza e stabilità, precedentemente enunciati, in questo contesto. Ponendo y_j=y(x_j) per ogni j=0,…,n, lo schema è detto consistente se, posto

,

si ha che τ(h)=max_j∣τ_j (h )∣→0 per h→0. Esempi significativi sono forniti dal metodo di Euler in avanti (EA), u_{j +1}−u_j=hf (x_j, u_j), e dal metodo dei trapezi o di Crank-Nicolson (CN), u_j+1−u_j=(h/2)[f (x_j,u_j)f (x_j+1,u_j+1)]. Per l'analisi dell'errore di discretizzazione locale τ_j (h) si ricorre al teorema di Taylor: poiché f(x_j,y_j)=y′ (x_j), si ottiene che τ(h)=O(h) per EA, mentre τ(h)=O(h²) per CN. Diremo che il problema numerico è convergente, se la soluzione numerica {u_j} converge a quella esatta nei nodi, ovvero se ∣y(x_j)−u_j∣≤C(h) per ogni j, C(h) essendo un infinitesimo quando h→0. Nel caso in cui un metodo converga, generalmente si ha che C(h)=Ch^p, dove p è l'ordine di infinitesimo di τ(h).

Pertanto, l'analisi dell'ordine di accuratezza di un metodo numerico si può ricondurre all'analisi dell'errore di troncamento locale. Sappiamo che la consistenza non è sufficiente a garantire la convergenza, richiedendosi anche la stabilità. Quest'ultima (detta anche zero-stabilità) si traduce nella richiesta seguente: per ogni b>x₀, h>0, sia N(h) il numero di nodi in [x₀,b] e cioè x_j=x₀+jh, con x_N≤b. Se {u_j, j=1,…,N(h)} e {v_j, j=1,…,N(h)} sono le successioni generate dal metodo numerico a partire da due diversi valori iniziali differenti, u₀ e v₀, allora esiste una costante K, dipendente eventualmente da b, taleche per ogni h sufficientemente piccolo si abbia ∣u_j−v_j∣≤K∣u₀−v₀∣ per ogni j=1,…,N(h). A titolo esemplificativo, consideriamo il metodo EA. Vale l'identità y_j−u_j=(y_j−y*_j)+(y*_j−u_j), dove y_j* è definito dalla relazione y_j*−y_j=hf(x_j,−1, y_j−1) ovvero è la soluzione di EA supponendo di conoscere in x_j−1 la soluzione esatta. Dalla definizione di τ_j(h) discende che y_j*−y_j−1=hτ_j(h), grandezza che esprime l'errore introdotto al passo j-esimo. Evidentemente la quantità globale di errore introdot-ta in [x₀,b] non potrà superare N(h)[hτ(h)], ovvero (b−x₀)τ(h). Peraltro, y_j*−u_j=h[f(x_j−1,y_j−1)−f(x_j,₋₁,u_j−1)] e, essendo f lipschitziana con costante L rispetto al secondo argomento, si avrà ∣y_j*−u_j∣≤hL∣y_j−1−u_j−1∣ (una relazione che può considerarsi inerente alla stabilità del metodo, in quanto esprime la variazione della soluzione numerica in rapporto a quella sui dati al generico passo j-esimo). Posto allora e_j=∣y_j−u_j∣, si ha la relazione ricorsiva e_j〈hτ(h)+hLe_j−1 per ogni j, la quale consente di concludere che e_j≤Cτ(h) per ogni j=1,…,N(h) con C=[exp(b)−1]/L, evidenziando come anticipato il contributo sinergico di stabilità e consistenza di un metodo numerico.

Il limite intrinseco del precedente concetto di zero-stabilità sta nella possibile dipendenza esponenziale della costante K da b; questa dipendenza rende tale proprietà inadeguata a governare comportamenti su intervalli di integrazione grandi o addirittura illimitati. In tal caso sarà opportuno richiedere che il metodo sia assolutamente stabile, ovvero che la soluzione {u_j} del problema modello y′(x)=λy(x) per x>0, con y(0)=1 e Reλ〈0, tenda a zero per x_j→∞. Nel caso di EA si ha u_j+1=(1+hλ)u_j e pertanto u_j=(1+hλ)j; la condizione di stabilità assoluta diviene ∣1+hλ∣〈1, ovvero hλ deve appartenere al cerchio di raggio unitario e centro (−1,0) nel piano complesso. Ciò induce una limitazione su h del tipo h〈2∣Reλ∣/∣λ∣² e il metodo EA verrà detto condizionatamente assolutamente stabile. Al contrario, il metodo CN soddisfa la relazione u_j=[(1+hλ)/(1−hλ)]^j per ogni j, e pertanto u_j→0 per x_j→+∞ incondizionatamente rispetto ad h. I metodi che godono di questa proprietà vengono detti A-stabili e sono appropriati per integrare equazioni differenziali su intervalli illimitati e anche sistemi differenziali di tipo stiff, ovvero sistemi la cui soluzione ha componenti che decadono nel tempo con dinamiche molto diverse.

Equazioni alle derivate parziali

La modellistica numerica e computazionale è di interesse primario in questo settore, la cui vastità non consente una sintesi soddisfacente in poche righe. Faremo un cenno alle più comuni metodologie di approssimazione. Se Ω⊂ℝ^d è una regione limitata del piano (d=2) o dello spazio (d=3), molti problemi fisici si possono modellare con il seguente problema matematico: trovare una funzione u (scalare o vettoriale) dipendente dal tempo e dallo spazio tale che ogni x=(x₁,..., x_d)∈Ω e t ›0 valga

[8] formula

con u=u₀ assegnata al tempo iniziale t=0. Il simbolo ∂/∂t esprime la derivata parziale rispetto alla variabile t (con x fissato), mentre per ogni funzione vettoriale w=w(x,t) la divergenza è definita da

(dove ∂/∂x_i è la derivata parziale lungo la direzione x_i). L'identità precedente esprime una legge di conservazione (o un sistema di leggi di conservazione nel caso vettoriale). In effetti, integrando la [8] su ogni sottoregione T di Ω, grazie al teorema della divergenza di Gauss si ottiene:

[9] formula

avendo indicato con Γ il bordo di T e, per ogni x∈Γ, con n=n(x) il versore di componenti n_i esterno a Γ (ovvero il vettore di modulo unitario perpendicolare al piano tangente a Γ nel punto x). Infine, f(u) è una funzione vettoriale, a d componenti f₁(u),…, f_d(u), detta flusso di u, e

La relazione precedente esprime la conservazione di u nella sottoregione T; questo significa che la variazione temporale del suo integrale ∫_Tudx è compensata dal bilancio di flusso attraverso la frontiera.

Sia {T} una partizione di Ω di elementi poligonali (triangoli o tetraedri) non sovrapponentisi. Più precisamente, due elementi distinti di {T} possono avere in comune solo vertici, lati e facce, e la loro unione ricopre interamente Ω. Il metodo ai volumi finiti è basato sulla proprietà di conservazione, imposta su ogni sottoregione T (detta volume finito). Per ogni coppia di volumi finiti adiacenti T_i e T_j, detta Γ_ij l'interfaccia fra T_i e T_j, i flussi normali su Γ_ij sono deputati a stabilire le relazioni di interdipendenza fra i valori delle incognite uⁱ=u∣_Ti e u^j=u∣_Tj (generalmente supponendo uⁱ costante su T_i, per ogni i). Tipicamente avremo

[10] formula

dove la somma è estesa a tutti gli indici j per i quali T_j è adiacente a T_i, mentre f_ap(uⁱ,u^j) è una conveniente approssimazione del flusso normale f(u)∙n su Γ_ij.

Il metodo delle differenze finite si basa invece sulla sostituzione delle derivate spaziali ∂/∂x_i in [8] con opportuni rapporti incrementali in nodi allineati lungo la i-esima direzione coordinata (analogamente a quanto fatto precedentemente per approssimare altre derivate). Infine, il metodo degli elementi finiti viene derivato dalla forma [8], supponendo che u sia approssimata con una funzione u_h la cui restrizione a ogni T (stavolta detto elemento finito) sia un polinomio di grado 1 (o più elevato), continuo sulle interfacce e soluzione del problema

[11] formula

dove v_h è una funzione (della sola x) polinomiale su ogni T dello stesso grado di u_h, f_h(u_h) un'opportuna approssimazione di f(u_h) e g esprime l'eventuale contributo del flusso normale (qualora venga assegnato) sulla frontiera fisica ∂Ω della regione Ω. Per flussi f_h(u_h) di forma complessa, gli integrali richiederebbero di essere approssimati numericamente. Nelle notazioni precedenti, h indica la massima lunghezza dei lati dei triangoli T, così che u_h→u per h→0. L'approssimazione agli elementi finiti si ispira alla cosiddetta formulazione debole del problema [8], formulazione che (nel caso di problemi stazionari e simmetrici) esprime a livello discreto il principio dei lavori virtuali: le v_h sono quindi le approssimanti dei cosiddetti spostamenti virtuali. Risulta evidente che, per l'effettiva risoluzione dei problemi sopra riportati, converrà discretizzare anche la derivata temporale, utilizzando per esempio schemi alle differenze finite (esplicite o implicite) come visto sopra nel trattamento di equazioni differenziali ordinarie del primo ordine, oppure lo stesso metodo agli elementi finiti. Nel caso implicito, l'equazione [11] genererà per ogni livello temporale un sistema di equazioni per la cui soluzione si possono usare le tecniche numeriche illustrate prima.

Strategie multi-livello

Come si è visto in molte situazioni, per l'approssimazione di problemi differenziali (siano essi ordinari o alle derivate parziali) si è ricondotti alla soluzione di sistemi lineari della forma A_hx_h=f_h, dove x_h indica il vettore delle incognite nodali di una griglia di calcolo la cui ampiezza caratteristica è h, mentre f_h e A_h indicano rispettivamente il termine noto e la matrice associati al sistema. Se si usa un metodo iterativo (quale il metodo di Jacobi o quello di Gauss-Seidel), si osserva che poche iterazioni sono sufficienti per abbattere le alte frequenze dell'errore e^k=x^k_h−x_h, mentre per la riduzione delle basse frequenze servirebbero moltissime iterazioni (x^k_h indica l'approssimazione di x_h dopo k  iterazioni). Allo scopo di accelerare la convergenza si può ricorrere a un problema ausiliario A_Hx_H=f_H, che possiamo immaginare associato alla discretizzazione dello stesso problema, ma su una griglia più rada di ampiezza caratteristica H>h.

A ogni vettore v_H, composto da valori nodali sulla griglia rada, possiamo associare un vettore v_h=I_hv_H composto da valori nodali sulla griglia fine originaria. Tipicamente, I_h è un processo di interpolazione rappresentabile con una matrice rettangolare. Indichiamo con I^t_h la matrice trasposta di I_h, che rappresenta dunque il processo di restrizione dalla griglia fine alla griglia rada. Indichiamo inoltre con Q_H la matrice la cui inversa è

e con Q_h la matrice A_h o un suo conveniente precondizionatore. Per la risoluzione del sistema originario si può usare il metodo iterativo che illustriamo di seguito. Se u^k_h è nota (per k≥0), si definisca u_h^k tramite la soluzione del sistema lineare (sulla griglia rada)

[12] formula

e quindi si definisca u_h^k come soluzione del sistema (sulla griglia fine)

[13] formula.

Combinando i due processi si trova che

[14] formula,

ovvero u_h^k è il risultato di una singola iterazione di Richardson sul problema originario, dove si introduce il precondizionatore P tale che P⁻¹=Q_H⁻¹+Q_h⁻¹−Q_h⁻¹A_hQ_H⁻¹. Si ritrova in questo modo il metodo multigriglia nella sua versione più semplice (a due livelli). I metodi a più livelli sono ottimali dal punto di vista della complessità computazionale, in quanto per la risoluzione del sistema originario richiedono un numero di operazioni proporzionale al numero di incognite (ovvero al numero di righe della matrice A_h). Una versione ridotta del metodo multilivello più adatta a calcolatori di tipo multi-processore si ricava sostituendo P con P_par, dove P_par⁻¹=Q_H⁻¹+Q_h⁻¹ si ottiene trascurando l'interazione non lineare fra Q_H⁻¹ e Q_h⁻¹. I cosiddetti metodi di decomposizione per sottodomini (o sottoregioni), introdotti a metà degli anni Ottanta del Novecento per la risoluzione parallela di problemi differenziali, possono essere formulati come esempi notevoli di tali procedure.

Bibliografia

Atkinson 1989: Atkinson, Kendall E., An introduction to numerical analysis, 2. ed., New York, Wiley, 1989.

Eriksson 1996: Eriksson, Kenneth e altri, Computational differential equations, Cambridge-New York, Cambridge University Press, 1996.

Golub, Van Loan 1989: Golub, Gene H. - van Loan, Charles F., Matrix-computations, 2. ed., Baltimore (Md.), Johns Hopkins University Press, 1989.

Lambert 1991: Lambert, John D., Numerical methods for ordinary differential systems. Initial value problem, Chichester, Wiley, 1991.

Quarteroni 2002: Quarteroni, Alfio - Sacco, Riccardo - Saleri, Fausto, Matematica numerica, 2. ed., Milano, Springer, 2002.

Quarteroni 2006: Quarteroni, Alfio, Modellistica numerica per problemi differenziali, 3. ed., Milano, Springer, 2006.

Quarteroni, Saleri 2006: Quarteroni, Alfio - Saleri, Fausto, Introduzione al calcolo scientifico, 3. ed., Milano, Springer, 2006.

Quarteroni, Valli 1994: Quarteroni, Alfio - Valli, Alberto, Numerical approximation of partial differential equations, Berlin-New York, Springer, 1994.

Quarteroni, Valli 1999: Quarteroni, Alfio - Valli, Alberto, Domain decomposition methods for partial differential equations, Oxford-New York, Clarendon, 1999.

Saad 1996: Saad, Yousef, Iterative methods for sparse linear systems, Boston (Mass.)-London, PWS, 1996.

Smith 1996: Smith, Barry - Bjørstad, Petter - Gropp, William, Domain decomposition, Cambridge-New York, Cambridge University Press, 1996.

Van der Vorst 2003: van der Vorst, Henk A., Iterative Krylov methods for large linear systems, Cambridge, Cambridge University Press, 2003.