stereografia
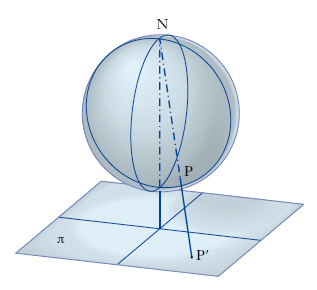
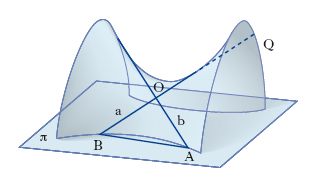
stereografia matematica In geometria, metodo di rappresentazione grafica di un solido sopra un piano. Proiezione stereografica di una sfera Fissato un punto N (polo) su una sfera (fig. 1) e un piano π parallelo al piano tangente alla sfera in N, si fa corrispondere a un punto generico P della sfera la sua proiezione P′ fatta da N sul piano. Si realizza così una corrispondenza biunivoca tra i punti del piano e i punti della sfera. Essa gode di notevoli proprietà geometriche: a) le circonferenze esistenti sulla sfera vengono proiettate su π in circonferenze (fanno eccezione le circonferenze per il punto N, che si trasformano in rette); b) si conserva l’angolo di due curve tracciate sulla sfera (si tratta quindi di una proiezione isogonale o conforme), proprietà quest’ultima che la rende particolarmente utile in cartografia, per es. nella costruzione del planisfero. La proiezione stereografica della sfera per le applicazioni alla cartografia si può far risalire a Ipparco di Nicea. Proiezione stereografica di una quadrica Proiezione dei punti di una quadrica Q irriducibile sopra un piano generico π eseguita da un punto O (fig. 2) appartenente a Q (ma non a π). La corrispondenza così stabilita tra la quadrica Q e il piano π (estensione della proiezione stereografica di una sfera) risulta generalmente biunivoca; si presentano infatti come eccezioni alla biunivocità: i punti delle due rette a, b appartenenti alla quadrica e passanti per O, i quali si proiettano nel punto A, o B, intersezione di a (o b) col piano π, e il punto O cui corrisponde su π la retta A B; viceversa gli elementi eccezionali sul piano π sono i punti A, B e la retta A B. Le ∞3 sezioni piane della quadrica si proiettano nelle ∞3 coniche di π passanti per A, B (se la sezione passa per O la conica proiezione si spezza nella retta A B e in un’altra retta di π). L’importanza teorica di una tale corrispondenza tra una quadrica e un piano sta nel fatto che lo studio delle curve e della loro geometria sopra una quadrica si può ricondurre a quello di particolari sistemi di curve piane.
In cartografia, proiezione stereografica polare, la proiezione stereografica della sfera terrestre in cui si assume come centro di proiezione un polo; i meridiani sono rappresentati da rette, i paralleli da circonferenze concentriche. Nella proiezione stereografica equatoriale si assume come centro di proiezione un punto dell’equatore; i meridiani si rappresentano mediante circonferenze passanti per le proiezioni dei poli, i paralleli mediante circonferenze ortogonali alle precedenti. medicina Tecnica diagnostica (detta anche röntgenstereografia e stereoradiografia) per lo studio morfologico e topografico degli organi, in condizioni normali e patologiche, e in particolare per lo studio dei segmenti ossei (cranio ecc.).