trisezione
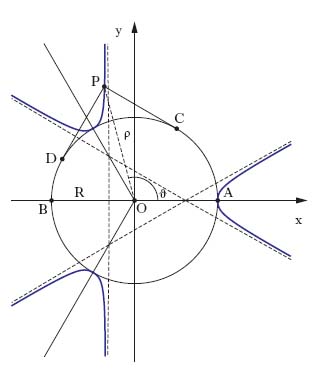
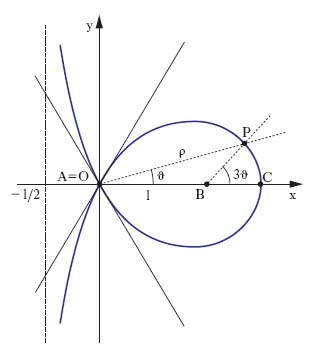
Divisione in tre parti tra loro uguali. Problema della t. dell’angolo Problema classico della geometria greca, consistente nella divisione di un angolo α in tre parti uguali. Se l’angolo α è dato mediante il suo coseno, cosα =a, il problema si riduce alla risoluzione dell’equazione di 3° grado cosα =4 cos3(α/3)−3 cos(α/3), cioè all’equazione 4x3−3x−a=0 ove si è posto x=cos(α/3). Si è dimostrato poi che il problema è irrisolubile (salvo che per particolari casi di α) con riga non graduata e compasso; sono tuttavia note soluzioni, alcune delle quali risalenti a geometri greci, qualora si supponga che sul foglio siano già disegnate particolari curve, dette appunto trisettrici, di cui sono esempi: la trisettrice di Longchamps e quella di Maclaurin. Trisettrice di Longchamps Fissati sopra un cerchio di raggio R (fig. 1) due punti diametralmente opposti A, B, si considerino due punti variabili C, D tali che l’arco AC sia doppio dell’arco DB; il luogo del punto d’incontro P delle tangenti al cerchio in C, D è la trisettrice di Longchamps. L’equazione polare della curva è ρ=R/cos3ϑ; dall’equazione cartesiana x(x2−3y2)=R(x2+y2) si rileva l’esistenza di tre asintoti e di tre assi di simmetria. Trisettrice di Maclaurin Fissati sopra una retta (fig. 2) i punti A, B, C, nell’ordine, è il
luogo dei punti P per cui PBC⋀ = 3PAB⋀.
Posto AB‾‾‾ = l, l’equazione polare della trisettrice risulta ρ=l sen3ϑ/sen2ϑ e l’equazione cartesiana 2x(x2+y2)=(3x2−y2)l; si tratta di una cubica circolare provvista di un nodo con tangenti a 60° e di un asintoto dato da x=−l/2; è un caso particolare della settrice di Plateau (➔ settrice).