isoperimetro
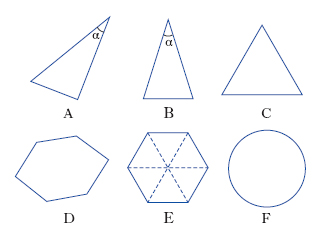
Il valore della lunghezza del contorno di figure piane aventi uno stesso perimetro; anche, il comune valore dell’area della superficie di solidi diversi. Problema degli isoperimetri (nel piano) Problema che consiste nel determinare quale sia la figura di area massima fra tutte le figure piane aventi per contorno una linea chiusa di data lunghezza, oppure tra figure isoperimetriche di una data specie (per es., poligoni con un dato numero di lati). Nello spazio si pone l’analogo problema di trovare, tra tutte le superfici chiuse aventi la medesima area, quella che racchiuda il massimo volume. Le figure che risolvono i vari problemi degli i. sono quelle cui compete la massima simmetria e regolarità: così tra i triangoli isoperimetrici aventi un angolo assegnato α (fig. 1A) ha area massima il triangolo isoscele (fig. 1B), mentre tra tutti i triangoli isoperimetrici ha area massima il triangolo equilatero (fig. 1C); tra i poligoni isoperimetrici di n lati (fig. 1D, per il caso n=6) quello di area massima è il poligono regolare di n lati (fig. 1E); infine, tra tutte le figure piane isoperimetriche il cerchio ha la massima area (fig. 1F), tra tutti i solidi isoperimetrici la sfera ha il massimo volume; ecc. Dal risultato ora citato per gli i. piani si deduce la disuguaglianza isoperimetrica: A≤L2/(4π) tra l’area A racchiusa da una curva chiusa e la sua lunghezza L (giacché L2/(4π) è l’area del cerchio la cui circonferenza ha lunghezza L).
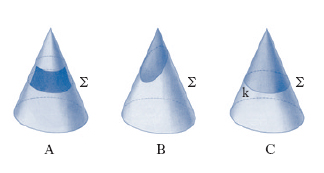
Il problema degli i. si può porre per figure appartenenti non a un piano, ma a una data superficie Σ; si domanda, cioè, di tracciare su Σ le linee chiuse di data lunghezza che racchiudano una porzione di Σ avente la massima area possibile. In questa formulazione generale il problema degli i. non è di semplice soluzione tranne che per superfici particolari. Per es., se Σ è un cono di rotazione (fig. 2) le linee cercate sono circonferenze situate su piani perpendicolari all’asse del cono (k in fig. 2C). I problemi degli i. rappresentano un primo esempio dei problemi trattati nel calcolo delle variazioni. Si tratta infatti di determinare i valori massimi di una grandezza (nel nostro caso l’area) che è funzione non di un parametro variabile, ma di una curva variabile (nel nostro caso la curva contornante, di lunghezza fissata).