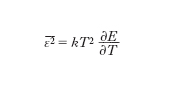fluttuazione

Ecologia

F. di una popolazione Andamento aperiodico della crescita di una popolazione. Una popolazione che ha raggiunto il limite massimo (➔ capacità) della densità numerica in un dato ambiente, può mostrare sia oscillazioni regolari sia f. attorno a questo limite: le prime normalmente rispecchiano una ben precisa dinamica della popolazione; le f., generalmente irregolari, vengono invece determinate di volta in volta dalla interazione dei fattori ambientali con fattori intrinseci alla popolazione stessa. Le f., di norma, sono stagionali e possono venire correlate alla variazione di uno o pochi dei maggiori fattori fisici limitanti l’ambiente (temperatura, precipitazioni ecc.).

Economia

Variazione dell’attività economica puramente accidentale, stagionale, a onda lunga, a carattere ricorrente; in senso più specifico il termine è riservato a questi due ultimi tipi, detti anche movimenti congiunturali o cicli economici.

Fisica

La differenza fra il valore ‘instantaneo’ di una data grandezza e il suo valore medio. In effetti, in fisica e nelle altre scienze sperimentali, usualmente si cerca una descrizione semplice dei fenomeni, basata sul presupposto che le grandezze a essi interessate abbiano un andamento regolare e siano rappresentabili con funzioni matematiche, possibilmente semplici. In realtà, però, qualunque grandezza è sempre una funzione assai irregolare di altre; per es., il valore istantaneo di qualunque grandezza è sempre una funzione irregolare del tempo e solo il suo valore medio su di un opportuno intervallo temporale ha un andamento regolare; spesso questa operazione di media è eseguita dai nostri strumenti di misura. Si hanno così f. di pressione, di densità e di altre grandezze fisiche, in un fluido le cui particelle siano soggette a un moto disordinato e incessante.

Molto spesso anziché di f. si parla di f. statistiche, per mettere in evidenza che esse sono proprie di fenomeni che si svolgono, nel tempo o nello spazio, secondo leggi statistiche.

La f. quadratica media ε^2̅̅̅̅ dell’energia E (cioè il valore medio del quadrato della differenza tra il suo valore istantaneo e il suo valore medio) di un sistema termodinamico in equilibrio termico con una sorgente di calore alla temperatura termodinamica T è, in particolare, data da

con k costante di Boltzmann. Applicando questa formula a un gas perfetto monoatomico, per il quale E = 3NkT/2 (con N numero totale di molecole), si ha ε^2̅̅̅̅=2E²/3N. Applicandola al calcolo delle f. d’energia della radiazione elettromagnetica in equilibrio termico in una cavità, A. Einstein (1909) ha mostrato che a tali f. contribuiscono due termini: uno, preminente alle basse frequenze, attribuibile a fenomeni interferenziali tipici delle onde; l’altro, preminente alle alte frequenze, analogo all’espressione appena ottenuta per il gas perfetto monoatomico e indicante quindi un comportamento corpuscolare. La presenza di questi due termini denuncia il carattere insieme ondulatorio e corpuscolare della radiazione elettromagnetica e costituisce una delle prime e più evidenti indicazioni del dualismo onda-corpuscolo. Teorema f.-dissipazione Teorema che fornisce una relazione fra le f. di un sistema in equilibrio e le proprietà dissipative dello stesso sistema quando venga a trovarsi (a causa di un forzamento esterno) fuori equilibrio. Classici esempi di tale relazione sono quella fra coefficiente di diffusione nel moto browniano di particelle in sospensione in un liquido e viscosità del liquido stesso (Einstein, 1905; ➔ moto) e la relazione fra rumore termico ai capi di un conduttore non percorso da corrente e la sua resistenza (effetto Johnson, o Johnson-Nyquist; ➔ rumore; Johnson, J.B.).

Medicina

L’insieme di movimenti passivi di una raccolta liquida (cavi ascessuali, cisti a contenuto liquido ecc.), quale si rivela ponendo il palmo di una mano in corrispondenza della parete della cavità, mentre l’altra mano imprime a questa delle compressioni ritmiche. La mano che sta ferma avverte delle pulsazioni o la sensazione che la massa aumenti di volume.