non lineare

Si dice di sistemi o fenomeni governati o associati a equazioni n.; un sistema n. è un sistema dinamico la cui evoluzione è regolata da equazioni n. nelle variabili che ne definiscono lo stato.

Elettronica

In un circuito, un elemento n. è genericamente un bipolo per il quale non sussista diretta proporzionalità tra tensione ai morsetti e intensità della corrente circolante: in particolare, un resistore n. non verifica la legge di Ohm (e perciò è detto anche non ohmico), mentre in un condensatore n. e in un induttore n. la capacità e l’induttanza, rispettivamente, variano con l’intensità della corrente.

Fisica

Il manifestarsi di un fenomeno n. in un sistema n. è intrinsecamente legato alla non linearità delle equazioni del mo;to (➔ meccanica); fenomeni n. sono per esempio il caos deterministico (➔ caos), i solitoni (➔ solitone), i fenomeni dell’ottica n. e dell’acustica n. (➔ ottica; suono).

Matematica

La trattazione di quei fenomeni in cui, non valendo un ‘principio di sovrapposizione’, non sono direttamente applicabili i metodi classici dell’analisi lineare costituisce l’oggetto dell’analisi n., applicabile a problemi sorti in vari campi applicativi, di varia natura ma aventi una comune struttura. Per es., in un’asta elastica finita incernierata a un estremo e soggetta nell’altro estremo a una compressione assiale, per piccole pressioni non si ha deformazione alcuna, mentre aumentando la pressione si raggiunge un valore critico, evidenziato da L. Euler, oltre il quale l’asta si flette bruscamente; problemi analoghi si presentano per la piastra elastica sottile studiata da T. von Kármán e l’arco elastico sottoposto a carichi. Altri problemi notevoli di analisi n. e instabilità sono stati trattati da J.-H. Poincaré (per trovare le configurazioni di equilibrio di una massa fluida omogenea ruotante), da G.I. Taylor, da H. Benard, da J. Watt e altri, in campi diversi, come nelle reazioni chimiche autocatalitiche con diffusione e nella trasmissione degli impulsi nervosi.

Uno dei problemi fondamentali dell’analisi n. è il seguente: dati due spazi di Banach e un’applicazione f(x, λ) (in genere dipendente da uno o più parametri λ) stabilire se l’insieme degli zeri dell’applicazione è non vuoto o, anche, data una applicazione trovare una coppia di spazi di Banach per cui l’insieme dei suoi zeri è diverso dall’insieme vuoto. In generale, data l’equazione

[1] f(x, λ) = 0,

fig.

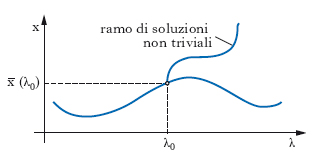
con f(x̄(λ₀), λ) = 0 per ogni λ, si dice che λ₀ è un punto di biforcazione (➔ biforcazioni, teoria delle), dalla soluzione x=x̄(λ₀) se in ogni intorno di (x̄(λ₀), λ₀) esiste qualche soluzione della [1] con x≠x̄. Le soluzioni della [1] che rappresentano uno stato noto del sistema, quale per es. di riposo o stazionario, si dicono soluzioni triviali, le altre non triviali. Da questo punto di vista acquistano interesse quei valori del parametro per i quali sorgono soluzioni non triviali; un punto è di biforcazione se in ogni suo intorno si trova una soluzione non triviale della [1]. I punti di biforcazione sono così quei valori critici del parametro in corrispondenza dei quali il sistema subisce vistosi cambiamenti di stato (v. fig.).