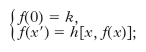ricorsività

ricorsività La proprietà di essere ricorsivo, cioè ricorrente. Teoria della r., o della ricorsione, o computabilità, la disciplina che si occupa di fornire una caratterizzazione matematica del concetto di algoritmo.

Teoria della ricorsività

La motivazione originaria per lo studio della r. fu soprattutto il problema della decisione per le teorie formali (formulato da E. Schröder nel 1895 e ripreso da L. Löwenheim nel 1915 e D. Hilbert nel 1918), cioè il problema se, per una data teoria formale T, esista un algoritmo per determinare se una formula A sia o non sia un teorema di T. Per studiare tale problema occorreva trovare un corrispettivo matematicamente preciso della nozione intuitiva di algoritmo. Lo sviluppo degli elaboratori ha poi fatto della r. un’area di studio rilevante anche per l’informatica: un programma per un elaboratore non è che un algoritmo espresso in un linguaggio comprensibile per quell’elaboratore. Perciò l’indagine con metodi matematici delle possibilità e dei limiti teorici degli elaboratori si riduce all’indagine di che cosa si possa e che cosa non si possa fare con metodi algoritmici.

Gli insiemi considerati nella teoria sono costituiti da numeri naturali o da n-ple di numeri naturali; tutte le funzioni sono da numeri naturali o da n-ple di numeri naturali in numeri naturali. Gli insiemi, e i predicati, si distinguono in decidibili (➔ decisione), computabili (➔ computabilità) e costruibili (un insieme I si dice costruibile se esiste un procedimento per raggiungere in un numero finito di passi qualunque elemento di I). I concetti di decidibilità, costruibilità e computabilità sono così strettamente collegati che, non appena si riesca a precisarne uno, gli altri due possono essere definiti in conseguenza. Generalmente si sceglie come concetto base quello di computabilità e si tenta di precisare il suo contenuto intuitivo definendo la classe delle funzioni computabili (o algoritmiche), cioè delle funzioni n-arie f tali che esiste un algoritmo per computare il valore f(x₁, …, x_n) per ogni n-pla di numeri naturali (x_s, …, x_n), dette funzioni ricorsive (o, meno spesso, recorsive). Queste si definiscono a partire da 3 funzioni iniziali mediante 3 regole. Le funzioni iniziali sono: la funzione zero z(x) = 0, la funzione successore s(x) = x+1 (simbolo x′), la funzione selezione i(x₁, …, x_n) = x_k(1≤k≤n). Le regole per ottenere nuove funzioni da quelle date sono: a) regola di sostituzione: date due funzioni f(x) e g(x), si può costruire la nuova funzione F(x) = f[g(x)]; b) regola di induzione: data la costante k e la funzione h(x,y), si può ottenere la funzione f(x) mediante il sistema di equazioni funzionali

c) regola di minimalizzazione che si esprime sia come minimalizzazione normale, sia come minimalizzazione limitata: per la regola di minimalizzazione normale, data la funzione g(x₁,x₂,y) e supposto che per ogni coppia (x₁,x₂) esista almeno un y tale che g(x₁,x₂,y) = 0, si può ottenere la funzione f(x₁,x₂) = μy[g(x₁,x₂,y) = 0] che si legge: f(x₁,x₂) pari al più piccolo y tale che sia g(x₁,x₂,y) = 0. Oppure anche, dato il predicato triadico P e supposto che per ogni coppia (x₁,x₂) esista almeno un y tale che la terna (x₁,x₂,y) convenga al predicato P, si può ottenere la funzione f(x₁,x₂) = μyPx₁x₂y. Per la regola di minimalizzazione limitata, con le stesse ipotesi precedentemente esposte si può ottenere la funzione

dove z dipende da x₁, x₂ con la convenzione (priva di significato intuitivo ma utile in pratica) che, se un tale y non esiste, f(x₁,x₂) = z. Per es., la funzione m.c.m. (x₁,x₂) può ottenersi per minimalizzazione normale o limitata dal predicato triadico Px₁x₂y: x₁ e x₂ sono divisori di y.

Si dicono funzioni ricorsive primitive le funzioni che si possono ottenere dalle funzioni iniziali mediante un numero finito di applicazioni delle regole di sostituzione e di induzione. Esempi di funzioni ricorsive primitive sono le comuni funzioni aritmetiche elementari: predecessore di x: pr(1) = 0, pr(x′) = x; segno di x: sg(0) = 0, sg(x′) = 1 (funzione caratteristica dell’insieme {0}); controsegno di x: sg(0) = 1, sg−−(x′) = 0 (funzione caratteristica dell’insieme di tutti i numeri naturali non nulli); fattoriale di x: 0! = 1, x′! = x!∙x′; somma di x e y: x+0 = x, x+y′ = (x+y)′; prodotto di x e y: x∙0 = 0, x∙y′ = x∙y+x; esponenziale di x e y: x⁰ = 1, x^y′ = x^y∙x; differenza aritmetica di x e y: x ∸ 0 = x, x ∸ y′ = pr(x ∸ y); differenza assoluta di x e y: |x−y| = (x ∸ y) +(y ∸ x); kroneckeriano di x e y: δ(x, y) = sg−−|x−y|; eguaglianza di x e y: ε(x, y) = sg|x−y|; minimo di x e y: min(x, y) = x ∸ (x ∸ y); massimo di x e y: max(x, y) = y ∸ (x ∸ y); resto della divisione di y per x: rst(r,0) = 0, rst(x, y′) = [rst(x, y)]′∙sg|x−[rst(x, y)]′|; quoziente della divisione di y per x: qz(x, 0) = 0, qz(x, y′) = qz(x, y)+ sg−−|x−[rst (x, y)] ′|. Un predicato a n posti è ricorsivo primitivo se tale è la sua funzione caratteristica. Esempi di predicati ricorsivi sono forniti da tutti i principali predicati aritmetici: eguale, x = y: funzione caratteristica ε (eguaglianza); diverso, x ≠y: funzione caratteristica δ (kroneckeriano); minore, x<y: funzione caratteristica sg(x′∸y); maggiore, x>y: funzione caratteristica sg(y′∸x); divisore, x|y: funzione caratteristica sg[rst(x, y)].

Accanto alle funzioni algoritmiche si possono considerare le relazioni algoritmicamente decidibili, cioè relazioni n-arie P tali che esiste un algoritmo per decidere se o meno P(x₁, …, x_n) valga, per x₁, …, x_n qualsiasi. Tali relazioni sono riducibili alle funzioni algoritmiche tramite la nozione di funzione caratteristica. Se P è una relazione n-aria, la funzione caratteristica di P è la funzione n-aria χ_P tale che χ_P(x₁, …, x_n) = 0 se P(x₁, …, x_n) vale, = 1 altrimenti. Si dice che una relazione P è ricorsiva se e solo se la sua funzione caratteristica χ_P è ricorsiva.

Teoremi di composizione di K. Gödel

I tre teoremi seguenti consentono di ottenere, dai precedenti, nuove funzioni e predicati ricorsivi primitivi. Teorema 1: le funzioni ottenute da funzioni o predicati ricorsivi primitivi mediante minimalizzazione limitata sono ricorsive primitive. Teorema 2: le funzioni ottenute da funzioni o predicati ricorsivi primitivi mediante distinzione di casi esaustivi e reciprocamente esclusivi sono ricorsive primitive. Teorema 3: i predicati ottenuti da predicati ricorsivi primitivi mediante connettivi enunciativi e quantificatori limitati sono ricorsivi primitivi. Questi teoremi sono importanti nel procedimento di aritmetizzazione, cioè di trasformazione dei predicati metateorici fondamentali in predicati aritmetici, allo scopo di poter riconoscere che essi sono ricorsivi primitivi. Si intravede, allora, come i teoremi di composizione di Gödel costituiscano un passo fondamentale per utilizzare la teoria della r. nei problemi di decisione. Infatti, avvenuta l’aritmetizzazione nell’ambito di un opportuno sistema formale del tipo di quello di Peano, constatare se un predicato metateorico, per es., è ‘dimostrabile’, è o meno verificato in un certo caso si riduce al calcolo – effettivamente eseguibile – di una funzione ricorsiva primitiva. Diventa a questo punto possibile, per es., la dimostrazione dei teoremi di indecidibilità e di incompletezza di Gödel. Va osservato comunque che sono stati trovati vari esempi di proposizioni vere (dette proposizioni combinatorie indecidibili) della teoria dei numeri, che non sono dimostrabili nell’aritmetica di Peano. Inoltre la classe delle funzioni ricorsive primitive non ricopre quella delle funzioni computabili. Infatti, già nel 1928 W. Ackermann aveva costruito una funzione computabile, ma non ricorsiva primitiva. Questa funzione, nota come funzione di Ackermann, utilizza un tipo di r. a incastro in cui non una, ma due variabili sono coinvolte nel procedimento di induzione.

R. generale

Si dicono ricorsive generali le funzioni che si possono ottenere dalle funzioni iniziali mediante un numero finito di applicazioni delle regole di sostituzione, induzione e minimalizzazione illimitata normale. È ovvio che la classe delle funzioni ricorsive generali contiene quella delle funzioni ricorsive primitive. È anche facile persuadersi che le funzioni ricorsive generali sono intuitivamente computabili. La tesi di A. Church (1936) afferma con argomentazioni suggestive, ma non inoppugnabili, che tutte le funzioni intuitivamente computabili sono ricorsive generali. Accolta questa tesi, risulta precisato il concetto intuitivo di computabilità e, conseguentemente, quello di decidibilità e di costruibilità.