stringa
In fisica, il più semplice oggetto dotato di estensione, compatibile con la relatività ristretta (detto anche s. o corda relativistica), che generalizza il concetto di particella puntiforme, nella teoria quantistica dei campi.
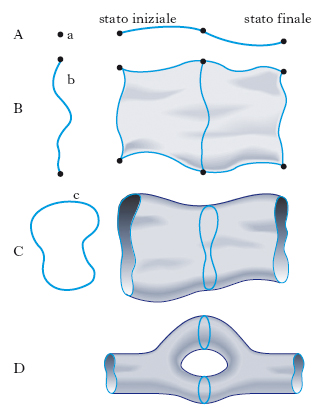
Mentre le particelle sono descritte da campi che dipendono dal punto nello spazio-tempo (fig. A), nelle teorie delle s. le particelle sono rappresentate dai modi di vibrazione di una s., ossia una struttura estesa unidimensionale, con estremi liberi (s. aperta, fig. B) o coincidenti (s. chiusa, fig. C), che descrivono un numero infinito di particelle il quadrato della cui massa (m2) cresce secondo multipli interi della tensione della stringa. Questa tensione T, parametrizzata anche con 1/α′, è l’unica costante dimensionale della teoria e quindi compare nella formula di massa: m2=(n/α′)+m02, dove n=0, 1, 2, ..., descrive lo spin massimo delle molte particelle che hanno la stessa massa m e m0 è una opportuna costante. La richiesta che i modi di vibrazione della s. relativistica rappresentino stati fisici impone condizioni così severe da determinare molte caratteristiche della teoria stessa: in particolare, condiziona la dinamica, imponendo la presenza di particelle di massa nulla, limita le possibili simmetrie interne che la teoria può avere e determina, persino, la dimensionalità dello spazio-tempo nel quale la s. può evolvere.
Questa dimensionalità critica è 26 per le s. bosoniche (che descrivono solo particelle con spin intero) e 10 per le superstringhe, o supercorde (cioè s. relativistiche nell’ambito di teorie supersimmetriche, che descrivono quindi particelle con spin sia intero sia semintero); ciò sembrerebbe escludere che queste teorie possano essere rilevanti per la nostra realtà quadridimensionale. La difficoltà è però solo apparente; infatti, queste teorie contengono la relatività generale e lo spazio-tempo gioca quindi un ruolo dinamico. È da questa dinamica che dovrebbe derivare la quadridimensionalità dell’Universo da noi osservato, cioè una metrica pressoché piatta nelle 4 dimensioni dello spazio-tempo usuale e una forte curvatura delle dimensioni aggiuntive: curvatura tale da impedire a oggetti macroscopici, di penetrare in esse, che resterebbero invece accessibili a particelle con energie proporzionali all’inverso del raggio di curvatura (tipicamente dell’ordine di 1019 GeV). La supersimmetria appare inoltre inevitabile: infatti, solo la versione supersimmetrica delle s. relativistiche, chiamata teoria delle superstringhe, è priva di tachioni, stati con massa quadra negativa, condizione intollerabile in una teoria coerente.
Che la relatività generale sia contenuta nella teoria delle s. si può mettere in evidenza osservando che tra le particelle di massa nulla, previste dalla teoria, ce n’è una di spin due, candidata ad avere il ruolo del gravitone. Il legame tra la teoria delle s. e le convenzionali teorie dei campi (tra le quali si annovera la gravità) è però più diretto. Come detto prima, oltre alle particelle senza massa la teoria prevede particelle massive. Se le energie che si considerano in un processo fossero assai più piccole dell’unica scala della teoria, ossia E2 ≪ 1/α′, allora le particelle massive non potrebbero essere eccitate e la descrizione si ridurrebbe a una teoria effettiva con solo particelle di massa nulla. Questa teoria effettiva è la teoria di Yang Mills per le s. bosoniche aperte, la teoria di pura gravità per quelle chiuse, e la teoria di supergravità per le superstringhe. Queste teorie dei campi appaiono quindi come il limite di basse energie della teoria delle s., valide quando la tensione della s. è tanto elevata che la struttura stessa della teoria non riesce a manifestarsi.
Le teorie effettive non possono essere portate al di là del loro limite di validità; in particolare, nel limite delle grandi energie la teoria delle s. si discosta da quella dei campi e in particolare dalla teoria quantistica della gravità, che, in questo limite, ha un comportamento che la rende gravemente inconsistente. La speranza di avere, con la teoria delle s., una struttura teorica coerente che contenga la gravità senza ereditarne le patologie, ha avuto un notevole incoraggiamento dall’analisi dello sviluppo perturbativo della teoria. Questo sviluppo è fondamentalmente diverso da quello delle normali teorie di campo.
Le s. possono spezzarsi o ricombinarsi con una probabilità misurata da un parametro adimensionale, g. Una s. aperta, che evolva nello spazio-tempo senza spezzarsi, descrive una superficie bidimensionale (chiamata superficie d’universo) che ha l’aspetto di una fascia (fig. B). Per una s. chiusa, la superficie d’universo ha una forma tubolare (fig. C). Se la s., evolvendo, si spezza in due per poi ricombinarsi di nuovo (ordine g2 rispetto al caso precedente), la superficie formata dalla s. ha l’aspetto di un tubo con una maniglia (fig. D). Questo permette d’intravedere come lo sviluppo perturbativo in g, ossia nella probabilità di spezzare e ricomporre, porti a una classificazione dei diagrammi di s. descritta da superfici di Riemann. Le singolarità delle ampiezze, così come eventuali divergenze, provengono da configurazioni limite, nelle quali le superfici cambiano topologia (perdendo una maniglia, strozzandosi in due superfici separate ecc.).