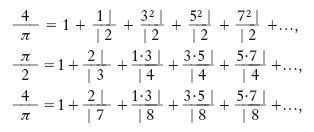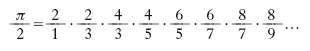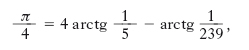pi
Sedicesima lettera dell’alfabeto greco (maiuscolo Π, minuscolo π) corrispondente al p latino.
Fisica
Il teorema π è il teorema fondamentale della similitudine meccanica, noto anche come teorema di Buckingham (➔ Buckingham, Edgar; similitudine).
Matematica
Il segno π (solitamente letto pi greco) è, come iniziale di περίμετρος (perimetro), il simbolo del numero che esprime il rapporto tra la lunghezza di una qualunque circonferenza e del relativo diametro. Esso interviene in formule riguardanti la circonferenza, il cerchio, la sfera e le altre superfici rotonde, nonché in relazioni con altre costanti matematiche e in legami fondamentali come la relazione di Eulero eiπ+1=0, e la formula di Stirling (➔ Stirling, James). Si tratta di numero reale irrazionale (cioè decimale illimitato non periodico) e anzi trascendente (non è cioè radice di nessuna equazione algebrica a coefficienti interi): 3,1415926535…. Nella pratica si usano in genere i valori approssimati
oggi si conoscono comunque sviluppi in serie che permettono, mediante l’uso di elaboratori, la determinazione di π con milioni di cifre decimali, esatte a meno di un numero finito di cifre.
Una prima valutazione di π è forse da attribuirsi ad Archimede; applicando il metodo dei perimetri ai poligoni di 96 lati egli ottenne la disuguaglianza 22/7<π<223/71. Il primo calcolo di un notevole numero di cifre decimali (35) di π è però dovuto a C. van Ludolph, per cui π era anche detto numero di Ludolph.
Sono qui elencati alcuni metodi utili per il calcolo effettivo di π; i primi quattro hanno però, più che altro, un interesse storico: a) metodo dei perimetri: si approssima la circonferenza di raggio R con poligoni regolari convessi inscritti e circoscritti; i loro perimetri formano due classi contigue, il cui elemento di separazione è 2Rπ; b) metodo delle aree: presi i poligoni come nel metodo precedente, le loro aree costituiscono due classi contigue, il cui elemento di separazione è R2π; c) metodo degli isoperimetri: fissata una lunghezza, per es. 2, si osserva che i raggi e gli apotemi dei poligoni regolari di perimetro 2 formano due classi contigue, il cui elemento di separazione è 1/π; d) metodo degli equivalenti: fissata un’area, per es. 1, si osserva che i quadrati dei raggi e degli apotemi dei poligoni regolari di area 1 formano due classi contigue, il cui elemento di separazione è 1/π; e) metodi basati sull’uso di algoritmi infiniti (frazioni continue, prodotti infiniti, serie). Delle seguenti tre espressioni di π mediante frazioni continue (➔ frazione)
,
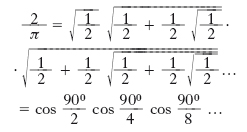
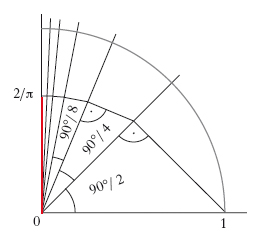
la prima è dovuta a W. Brouncker e le altre a L. Eulero. Tra le valutazioni di π mediante prodotti infiniti citiamo quella di F. Viète:
che dà luogo alla semplice costruzione geometrica indicata in figura. Ricordiamo inoltre quella di J. Wallis:
Infine, tra gli sviluppi in serie utilizzabili per il calcolo di π il più importante è forse quello dell’arcotangente:
,
dal quale, per x = 1 si ottiene
Questa serie converge però assai lentamente; una formula che viceversa permette un calcolo rapido delle prime cifre di π si ottiene dall’identità
,
utilizzando lo sviluppo in serie dell’arcotangente.