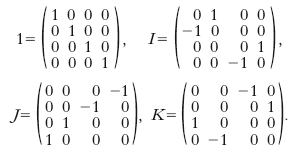quaternione
Particolare tipo di numeri che rappresentano una generalizzazione dei numeri complessi.
I q. costituiscono un corpo non commutativo e un’algebra non commutativa sul campo dei numeri reali. Introdotti da W.R. Hamilton nel 1843, hanno trovato numerose applicazioni in vari campi della matematica. Nell’algebra dei q., che si indica per solito con il simbolo H ciascun q. ha la forma a+bi+cj+dk, dove a, b, c, d sono numeri reali e i, j, k sono le cosiddette unità immaginarie. L’addizione si definisce nel modo usuale, mentre la moltiplicazione si basa sulle seguenti relazioni i2=j2=k2=−1, ij=−ji=k; jk=−kj=i, ki=−ik=j. I q. formano così un corpo non commutativo. In ogni q. q=a+bi+cj+dk si distinguono una parte reale Req=a e una parte immaginaria Imq=bi+cj+dk. Benché il prodotto dei q. non sia in generale commutativo, esso è tale se le parti immaginarie dei q. che si moltiplicano differiscono per un fattore di proporzionalità reale; in particolare ciò avviene se uno dei due q. si riduce alla sola parte reale (ossia se è un numero reale). Si chiama q. coniugato di q e si indica con q̄ il q. Req−Imq, ossia a−bi−cj−dk.
Il prodotto qq̄ è il numero reale a2+b2+c2+d2, che si chiama norma di q e si indica con N(q). La norma del prodotto di due o più q. è uguale al prodotto delle norme dei fattori e poiché l’unico q. di norma nulla è lo zero, si conclude che nell’algebra H vale il principio di annullamento del prodotto. Anche il coniugato del prodotto di più q. è uguale al prodotto dei coniugati dei fattori, ma l’ordine dei fattori risulta invertito, cioè (‾‾‾‾‾‾‾ q1q2…qn)=q̄n…q̄2q̄1: ciò significa che il coniugio (ossia l’applicazione di H in sé stesso che a ogni q. associa il q. coniugato) non è un automorfismo, a differenza del caso dei numeri complessi.
Un’altra proprietà dell’algebra H è di essere un’algebra con divisione: ciò significa che le equazioni qx=q′ e yq=q′ hanno sempre soluzione purché sia q≠0. A tal fine si introduce il q. q̄/N(q), che si chiama inverso di q. e si indica con q–1 perché qq–1=q–1q=1. Un celebre teorema di G.F. Frobenius (1878) stabilisce anzi che l’algebra H è la sola algebra con divisione non commutativa sul campo reale R.
È stato osservato che è possibile assegnare 4 matrici quadrate 1, I, J, K tali che abbiano la stessa tabella moltiplicativa delle 4 unità 1, i, j, k dei quaternioni. La cosa è anzi realizzabile in più modi; una prima possibilità, scoperta da J.J. Sylvester, è:
È stato dimostrato (da S. Bochner) che non esistono 4 matrici quadrate di ordine 3 la cui tabella moltiplicativa corrisponda a quella di 1, i, j, k, mentre per quelle di ordine 4 vi sono varie soluzioni; per es.:
Le matrici di cui sopra hanno utilizzazione nella teoria quantistica e nella fisica atomica e precisamente nella teoria di Dirac delle equazioni d’onda relativistiche dell’elettrone.
Un risultato importante è che ogni equazione algebrica a coefficienti quaternionali ha sempre almeno una radice costituita da un q. (teorema di Eilenberg e Niven).
Il corpo H può ricevere una struttura topologica (basata sulla nozione di norma di un q.) diventando così uno spazio topologico, anzi, poiché le operazioni di somma e di prodotto in H risultano continue, un corpo topologico. Si tratta poi di un corpo topologico connesso e anche localmente compatto (cioè, nonostante H non sia compatto, tuttavia ogni suo punto ha un intorno la cui chiusura è compatta): l’importanza di questi caratteri sta nel fatto che essi garantiscono la validità dei teoremi fondamentali dell’analisi classica (per es., il teorema di B. Bolzano-K. Weierstrass) e quindi la possibilità di sviluppare un calcolo infinitesimale. Ebbene, un celebre teorema di L.S. Pontrjagin (1932) afferma che gli unici corpi topologici connessi e localmente compatti sono il corpo R dei numeri reali, il corpo C dei numeri complessi e il corpo H dei quaternioni.