elastoplasticità

elastoplasticità Proprietà dei corpi naturali suscettibili di deformazioni di tipo elastico associate a deformazioni di tipo plastico, quando siano assoggettati a opportune sollecitazioni. Con la stessa denominazione, o con quella di teoria dell’e. o della plasticità, si designa anche quella parte della scienza delle costruzioni che studia la statica dei sistemi resistenti in condizioni elastoplastiche.

Nell’e. si affronta lo studio statico di strutture per le quali non è accettabile l’ipotesi che il comportamento dei materiali sia perfettamente elastico; per esse cioè non può ritenersi verificata la proporzionalità diretta tra tensioni e corrispondenti deformazioni unitarie (legge di Hooke; ➔ elasticità). È perciò necessario anzitutto precisare qual è il legame tra tensioni e deformazioni. In particolare occorre precisare la legge di variazione della deformazione e in funzione della tensione normale σ con riferimento alla sollecitazione di trazione o di compressione semplice, che è il tipo di sollecitazione cui più comunemente si ricorre nelle prove di resistenza meccanica dei materiali da costruzione. Queste prove confermano la validità della legge di Hooke finché la tensione σ si mantiene inferiore al limite di proporzionalità, superato il quale il diagramma della funzione ε = f (σ) si discosta dall’andamento lineare, presentando caratteristiche diverse a seconda dei materiali.

fig

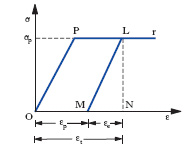
Una prima distinzione dei materiali in duttili e fragili è suggerita in particolare dalla forma del diagramma di prova a seconda che essa riveli o no la presenza della fase di snervamento, cioè una fase in cui la deformazione elastoplastica aumenta spontaneamente senza apprezzabili variazioni della tensione σ. Le caratteristiche con cui si presenta lo snervamento sono in realtà diverse da materiale a materiale, e spesso dipendono, anche per uno stesso materiale, dalle modalità di esecuzione delle prove, ma è indispensabile una schematizzazione se si vuol pervenire a una nuova espressione analitica semplice del legame tra ε e σ (v. fig.). Per i materiali duttili si ammette perciò, anzitutto, che la fase di snervamento cominci immediatamente dopo aver superato il limite di proporzionalità σ_p; cioè si ammette che durante tutta la fase di snervamento la tensione σ si mantenga costante (retta r), mentre aumenta la deformazione fino alla rottura: quanto dire che si assume come diagramma tensioni-deformazioni il diagramma schematico riportato in fig. Altri tipi di diagrammi schematici possono essere assunti per i vari materiali, ma quello cui normalmente si fa riferimento nelle applicazioni è quello indicato, poiché esso corrisponde alla schematizzazione più semplice e più soddisfacente per i più importanti materiali da costruzione. Nel diagramma è possibile riconoscere sia l’entità della deformazione plastica sia l’entità della deformazione elastica per ogni valore assegnato della deformazione totale (al disopra del limite di proporzionalità); l’esperienza mostra infatti che se si carica un provino fin oltre il limite di proporzionalità, la successiva fase di scarico presenta un andamento pressoché lineare con un coefficiente angolare uguale a quello della fase elastica. Se pertanto sul diagramma (σ, ε) s’individua il punto L corrispondente a un’assegnata deformazione unitaria e se per L si conducono la normale LN all’asse delle ε e la parallela LM al tratto OP della fase elastica, restano individuati sull’asse delle ascisse la deformazione plastica e la deformazione elastica che costituiscono l’assegnata deformazione totale. La frazione plastica è: ε_p = OM, e la frazione elastica è: ε_e = MN, risultando, naturalmente, ε_t = ε_p + ε_e. In base al diagramma è possibile, per es., affrontare il problema della determinazione delle tensioni interne di una struttura staticamente determinata per vincoli esterni, in regime elastoplastico.

È da tener conto, peraltro, che nel caso di strutture iperstatiche l’intervento delle deformazioni plastiche modifica le reazioni dei vincoli, e il calcolo di queste ultime diviene molto più complesso perché non è più valido il principio di sovrapposizione degli effetti; il calcolo delle reazioni sovrabbondanti può essere effettuato per tentativi, controllando se la deformazione complessiva, che corrisponde a certi valori assunti per le incognite iperstatiche, è compatibile o no con i vincoli. Si osserva poi che anche in regime elastoplastico sono validi i teoremi relativi al lavoro di deformazione quando si tenga conto, oltre che dell’energia potenziale elastica, anche del lavoro disperso per deformazioni plastiche: in tal caso tuttavia le equazioni che si ricavano dall’applicazione dei teoremi non sono più sufficienti alla determinazione delle iperstatiche (contrariamente a quanto avviene per il regime elastico), perché in esse compaiono altri parametri dipendenti dalla plasticità del materiale; anche per tale via occorre quindi ricorrere a metodi indiretti.

Molto numerosi sono i problemi ricollegabili alla teoria della e.: dallo studio delle autotensioni concomitanti a deformazioni plastiche, alla determinazione del coefficiente di sicurezza di una struttura rispetto alla rottura, dallo studio dei fenomeni di viscosità, alle applicazioni relative alla lavorazione dei metalli.