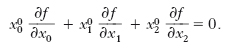polare

Matematica

Data una curva algebrica piana C, di ordine n, la cui equazione in coordinate omogenee sia f(x₀,x₁,x₂) = 0 e fissato comunque il punto P⁰(x⁰₀, x⁰₁, x⁰₂), si dice curva p. (o assolutamente p.) di P⁰ rispetto a C, la curva algebrica C′ di ordine n−1 che ha equazione

fig. 1

fig. 2

fig. 3A

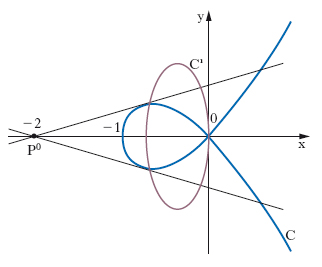
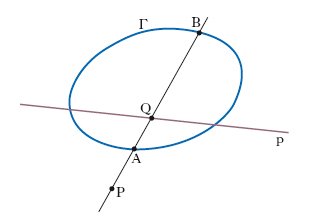
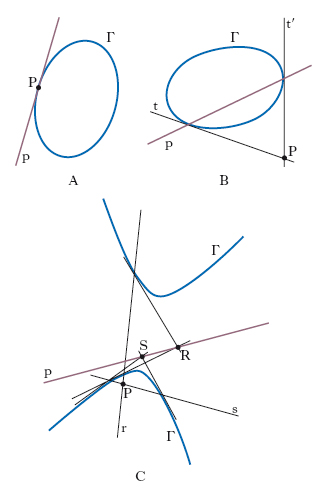
Una medesima curva C ha perciò ∞² curve p. (una per ogni posizione di P⁰ nel piano) che costituiscono una rete. Le p. di C hanno notevole importanza nello studio delle proprietà proiettive di C stessa. Anzitutto si osserva che la p. di P⁰ rispetto a C dipende solo da P⁰ e da C e non dalle coordinate di P⁰ e dall’equazione di C (elementi, questi, che sono in relazione anche agli assi coordinati). Inoltre essa contiene non solo tutti gli eventuali punti singolari di C ma anche i punti di contatto delle rette tangenti a C passanti per P⁰: in fig. 1, P⁰ ha coordinate (−2,0), C è la cubica y² = x²(x+1), C′ è l’ellisse y² = −5x²−4x, che è la p. di P⁰ rispetto a C. Hanno interesse anche le p. successive di una curva C: p. seconda di P⁰ rispetto a C è la p. di P⁰ rispetto a C′, e così via. In particolare la p. (n−1)-esima di P⁰ è una retta e se P⁰ è un punto di C è proprio la retta tangente a C in P⁰. È poi importante il teorema delle p. reciproche o legge di reciprocità, secondo il quale se la p. s-esima di P⁰ passa per P¹, la p. (n−s)-esima di P¹ contiene P⁰. Retta polare È la p. di un punto (polo) rispetto a una conica, ovvero più in generale, la p. (n−1)-esima di un punto rispetto a una curva Γ d’ordine n. Nel caso di una conica, la p. p di P è anche il luogo geometrico dei punti Q del piano tali che, dette A, B le intersezioni della retta PQ con Γ, i punti PQAB formino un gruppo armonico (fig. 2). Inoltre se P è un punto di Γ, p è la tangente in P a Γ (fig. 3A); se invece P è esterno a Γ, cioè se da esso si possono condurre a Γ due tangenti reali t, t′ (fig. 3B), la p. p è la retta che passa per i punti di contatto di t, t′; se, infine, P è interno a Γ (fig. 3C) la retta p si può ottenere come congiungente i poli R e S di due rette arbitrarie r, s per P.

Tecnica

fig. 4

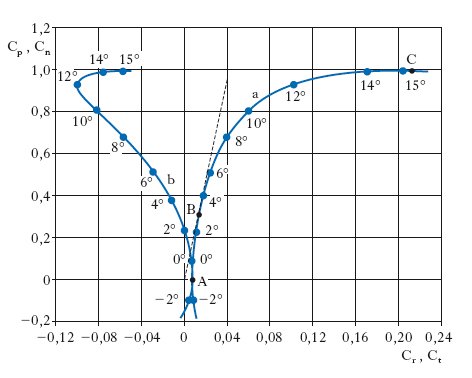
In aerodinamica, la p. assoluta (o fissa) è il diagramma che indica come varia il coefficiente di portanza C_p, in funzione del coefficiente di resistenza C_r per un dato corpo investito da una corrente fluida, uniforme a grande distanza dal corpo stesso (teoricamente a distanza infinitamente grande). Particolare interesse presentano le p. di profili alari, ali, fusoliere e scafi, parti di velivoli, velivoli parziali e completi, senza o con propulsore attivo ecc. Se il corpo ha una parte mobile (per es., ala con aletta o con alettone, equilibratore con stabilizzatore ecc.), vi sono tante p. quante sono le posizioni della parte mobile. Nella fig. 4 (curva a) è riportato l’andamento di una p. di una certa ala. Si nota un punto A in cui C_r è minimo, un punto C in cui C_p è massimo, un punto B di efficienza massima (dove il raggio vettore dall’origine è tangente alla p.). L’angolo di incidenza in B è quello che consente a un velivolo in volo planato (senza propulsore attivo) di percorrere il maggior percorso in aria dal punto di inizio della discesa; il rapporto C_p/C_r indica quante volte tale percorso è maggiore della quota relativa al terreno dell’aereo dal punto di inizio. Per le buone ali il tratto centrale della p. ha andamento sensibilmente parabolico. Per i corpi che hanno un piano di simmetria si hanno tante p. quanti gli angoli di deviazione; in questo caso si può avere una p. generalizzata includendo opportunamente il coefficiente di devianza C_d. Il diagramma del coefficiente dell’azione aerodinamica normale C_n in funzione del coefficiente dell’azione tangenziale C_t, valutati quindi rispetto ad assi solidali con il corpo, è detto p. relativa (o mobile). Ha importanza per i calcoli di robustezza del corpo, in particolare dell’ala, perché fornisce direttamente le forze aerodinamiche normali al piano alare e nel piano alare. Nella fig. 4 (curva b) è riportato l’andamento della p. relativa di un’ala.