influenza, linee di
Nella scienza delle costruzioni, particolari diagrammi che forniscono i valori delle sollecitazioni o delle deformazioni provocate da una forza in una data sezione trasversale di una struttura piana, al variare del punto di applicazione della forza (fermi restando, invece, intensità e orientamento della forza). La considerazione delle linee d’i. risulta soprattutto utile nella fase di progetto di una struttura (in particolare di un ponte), perché da esse è possibile dedurre le sollecitazioni massime che potranno verificarsi in tutte le diverse sezioni della struttura, per tutte le possibili posizioni dei carichi mobili.
Tracciamento delle linee d’influenza
Il tracciamento delle linee d’i. si effettua di norma per via diretta: si determinano cioè i valori dell’effetto in esame per un conveniente numero di posizioni del carico e si riportano in opportuna scala su un grafico, costruendo poi il diagramma per punti. Risulta ovviamente comodo riferirsi a una forza di grandezza unitaria, sicché il diagramma possa valere per una forza di intensità qualsiasi (purché dello stesso orientamento). Quando si tratti delle linee di i. delle sollecitazioni M, T, N (momento flettente, sforzo di taglio e sforzo normale), conviene spesso la preventiva determinazione delle linee d’i. relative alle componenti della reazione di un vincolo, perché da queste si deducono le prime ricordandone le corrispondenti espressioni in funzione di quelle.
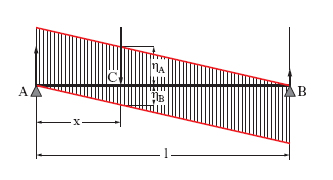
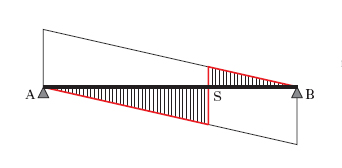
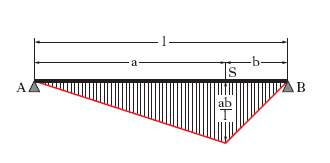
Nel caso dei sistemi piani staticamente determinati, le linee d’i. delle reazioni (e perciò anche quelle delle sollecitazioni nella generica sezione trasversale) sono costituite da segmenti rettilinei. Così, per es., per una trave orizzontale AB semplicemente appoggiata, di luce l, e soggetta a un carico verticale P, detta x la distanza del punto di applicazione della forza dall’estremo A, la reazione verticale in A vale in modulo P(l−x)/l. Si tratta di una espressione lineare in x, che fornisce, per P=1, l’equazione della linea d’i. della reazione in A. Analogamente per la reazione in B. Per entrambe sono riportate le linee d’i. nella fig. 1. Le ordinate ηA e ηB dei due diagrammi, lette in corrispondenza del generico punto C di applicazione del carico, forniscono i valori delle corrispondenti reazioni vincolari. Nella fig. 2 è indicato come dai diagrammi precedenti possa ottenersi la linea d’i. dello sforzo di taglio in una generica sezione S della trave, relativamente al medesimo carico verticale. Per la corrispondente linea d’i. del momento flettente in S si ha invece il diagramma triangolare indicato nella fig. 3, con valore massimo sotto la sezione S medesima e pari ad ab/l, dove a e b indicano le distanze di S rispettivamente da A e da B. Più complessa si presenta la determinazione diretta delle linee d’i. delle reazioni e delle sollecitazioni per i sistemi iperstatici. Il tracciamento viene allora di norma effettuato per punti e la determinazione delle reazioni iperstatiche corrispondenti alle diverse posizioni del carico è per lo più effettuata con il metodo dell’ellisse di elasticità (➔ Culmann, Karl).
Altri metodi
Esistono anche altri metodi generali validi per qualunque tipo di trave (sia staticamente determinata sia iperstatica) che riconducono la determinazione delle linee d’i. alla costruzione di particolari linee elastiche, corrispondenti a opportune condizioni. È sufficiente, per es., l’applicazione del teorema di Maxwell (➔ Maxwell, James Clark) per riconoscere che per una trave comunque vincolata la linea d’i. dell’abbassamento in una sezione S per effetto di un carico mobile verticale coincide con la linea elastica della trave relativa al medesimo carico posto sulla sezione S. Analogamente, la linea d’i. della rotazione in S, relativa a un carico verticale unitario, coincide con il diagramma degli spostamenti verticali provocati da un’unica coppia, di momento unitario, applicata nella sezione S. Da quanto sopra, risulta intanto evidente che le linee d’i. di spostamenti e rotazioni, anche per sistemi staticamente determinati, non possono avere andamento rettilineo.
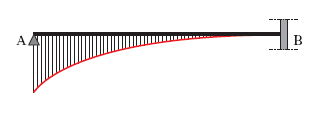
L’applicazione dello stesso teorema di Maxwell consente pure la determinazione della linea d’i. della reazione vincolare sovrabbondante per tutte le travi una sola volta iperstatiche. Così per es. (fig. 4), per una trave AB, incastrata in B e semplicemente appoggiata in A, la linea d’i. della reazione verticale in B per effetto di un carico verticale unitario coincide con la linea elastica della trave AB, svincolata in B e ivi soggetta a una forza verticale unitaria.
Per le linee d’i. dei carichi, quale che sia il tipo della trave, si può ricorrere al più generale metodo fornito dal teorema di Land: le linee d’i. delle sollecitazioni M, T, N nella generica sezione S di una trave coincidono con i diagrammi degli spostamenti verticali, subiti dai punti dell’asse, nella deformazione (distorsione) che si avrebbe tagliando la trave in S e applicando alle due facce due sistemi opposti di forze fittizie, capaci di produrre soltanto una rotazione relativa unitaria delle due facce (linea d’i. di M); o solo uno spostamento relativo unitario secondo la tangente all’asse della trave (linea d’i. di N); o solo uno spostamento relativo unitario secondo la normale all’asse della trave (linea d’i. di T). Il metodo di Land, e così pure i metodi generali per le linee d’i. di spostamenti e rotazioni, sono suscettibili di applicazioni sperimentali abbastanza semplici a mezzo di modelli. Questi sono costruiti con materiale sufficientemente elastico e in scala ridotta, tale che si abbia proporzionalità tra i momenti d’inerzia delle sezioni trasversali del modello e dell’originale; la misurazione degli spostamenti verticali dei punti dell’asse si effettua con microscopi.