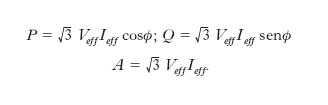trifase

trifase In elettrotecnica, sistema t., sistema di tre grandezze elettriche sinusoidali della stessa frequenza, per es., tre forze elettromotrici. La denominazione di t. è attribuita anche al circuito elettrico ove sono definite le tre grandezze considerate.

Circuiti trifase

fig. 1A

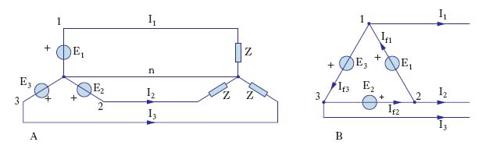
Ciascun elemento del circuito t., dove è definita una delle tre grandezze considerate, si dice fase e viene individuato da un numero d’ordine, in modo da determinare tra le fasi una certa sequenza. Una caratteristica di un sistema t. è il modo con cui sono collegate tra loro le singole fasi. Facendo riferimento, per es., a tre generatori di forza elettromotrice (f.e.m.), questi possono essere collegati tra loro in due modi per costituire un generatore t.: a) collegamento a stella (fig. 1A), se i tre inizi degli avvolgimenti dei singoli generatori sono collegati insieme per costituire il centro stella 0, mentre le tre estremità libere degli avvolgimenti dei generatori individuano i tre morsetti 1-2-3 da collegare alla linea; talvolta si utilizza come terminale anche il centro stella e lo si collega con un quarto conduttore n, detto filo neutro; in questo caso il sistema si dice a stella con neutro, altrimenti si dice semplicemente a stella; b) collegamento a triangolo (fig. 1B), se l’inizio di un generatore è collegato alla fine di quello successivo; i tre morsetti 1-2-3 che così si individuano vengono collegati alla linea; in questo caso però è necessario verificare che la somma delle f.e.m. sia nulla, altrimenti si ha entro il triangolo una corrente di circolazione che è limitata soltanto dalle impedenze interne dei generatori stessi. Come appare chiaro, l’uso di soltanto tre (o, con il neutro, quattro) fili per la trasmissione costituisce un primo, grande vantaggio rispetto a un equivalente sistema di tre linee monofase.

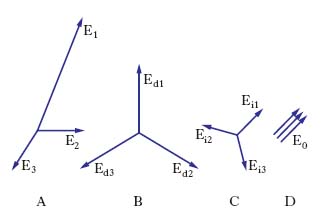
Un sistema t. di grandezze elettriche si dice simmetrico se le tre grandezze hanno la stessa ampiezza e sono sfasate fra loro di un terzo di periodo, altrimenti si dice asimmetrico. Il sistema è detto simmetrico di sequenza diretta se è la fase 2 a essere sfasata in ritardo di 1/3 di periodo rispetto alla fase 1, mentre rispetto a quest’ultima la fase 3 è sfasata di 2/3 di periodo; è detto invece simmetrico di sequenza inversa se è la fase 3 a essere sfasata in ritardo di 1/3 di periodo rispetto alla fase 1. Un sistema t. si dice puro se la somma delle tre grandezze è uguale a zero.

fig. 2

fig. 3A

Ricorrendo alla rappresentazione con il metodo vettoriale per le grandezze sinusoidali, in fig. 2 è rappresentato il diagramma vettoriale delle tre f.e.m. di fig. 1A, nel caso che esse costituiscano un sistema t. simmetrico (di sequenza diretta), e il diagramma vettoriale delle tre correnti I₁, I₂, I₃ nella linea per il carico di fig. 1A, in cui ϕ rappresenta l’angolo caratteristico delle impedenze Z. Si dice anche normalmente che le correnti costituiscono un sistema t. equilibrato e che il carico è equilibrato poiché formato da tre impedenze eguali; in caso contrario il carico e le correnti sono squilibrati. Spesso la maggior parte degli studi riguardano sistemi t. simmetrici ed equilibrati, ovvero caratterizzati dal fatto che sia le tensioni sia le correnti costituiscono sistemi t. simmetrici. In tal caso è sufficiente limitare l’analisi al circuito di una sola fase. Nel caso generale, se il sistema è lineare si applica il calcolo delle componenti simmetriche basato sul teorema di C.L. Fortescue, in base al quale un sistema di grandezze t. (rappresentabili con tre vettori, fig. 3A) può essere pensato come la somma di un sistema t. simmetrico di sequenza diretta (terna di vettori di fig. 3B), di un sistema t. simmetrico di sequenza inversa (terna di vettori di fig. 3C) e di un sistema t. di sequenza zero (o omopolare, terna di vettori di fig. 3D), caratterizzato quest’ultimo dal fatto che le grandezze sono di uguale ampiezza e in fase tra loro. Applicando il principio di sovrapposizione degli effetti, ci si riduce allo studio di tre sistemi monofase.

Tensioni concatenate e correnti di linea

Nei sistemi t., oltre a parlare di tensione e di corrente di fase (che sono quelle relative a una fase del circuito) si introducono normalmente anche le tensioni concatenate e le correnti di linea. Nel caso di collegamento a stella tra tensioni concatenate V e tensioni di fase E valgono le relazioni: V₁₂=E₁−E₂; V₂₃=E₂−E₃; V₃₁=E₃−E₁; se il sistema delle tensioni di fase è simmetrico, le tensioni concatenate sono eguali e pari a √‾‾‾3 volte il valore di quelle di fase. Nel caso di collegamento a triangolo si ha coincidenza tra tensioni concatenate e di fase: V₁₂=E₁; V₂₃=E₂; V₃₁=E₃. Sono chiamate tensioni stellate, o stellari, quelle che si hanno ai capi di una terna di impedenze eguali collegate a stella; per un sistema t. con neutro sono quindi le tensioni tra ciascun conduttore e il neutro. Per quanto riguarda le intensità, le correnti di linea I_l coincidono con le correnti di fase I_f nel caso di collegamento a stella, mentre nel caso di collegamento a triangolo valgono le relazioni: I₁=I_f1−I_f3; I₂=I_f2−I_f1; I₃=I_f3−I_f2; se il sistema delle correnti è simmetrico, le correnti di linea hanno intensità pari a √‾‾‾3 volte quella delle correnti di fase. In un sistema t. simmetrico ed equilibrato la potenza istantanea erogata dal generatore t. o assorbita complessivamente dal carico è costante nel tempo a differenza di quanto accade nei sistemi monofase in cui è variabile. È questo un secondo grande vantaggio che un sistema t. presenta rispetto ai sistemi monofase. La potenza attiva P vale in un sistema t. simmetrico ed equilibrato 3E_effI_effcosϕ, essendo E_eff, I_eff i valori efficaci delle tensioni e delle intensità di corrente e ϕ l’angolo di sfasamento relativo; la potenza reattiva Q vale 3E_effI_effsenϕ, mentre la potenza apparente A vale 3E_effI_eff. In luogo delle espressioni sopra riportate generalmente si considerano la tensione concatenata V e l’intensità I della corrente di linea; si dimostra che sia nel collegamento a stella sia nel collegamento a triangolo valgono le relazioni