predicibilità
predicibilità Il fatto di poter essere conosciuto anticipatamente. La possibilità di predire, almeno in linea di principio, il futuro con precisione arbitraria è stata considerata per molto tempo una caratteristica fondamentale del metodo scientifico, che aveva come modello ideale la concezione laplaciana dell’universo (➔ Laplace, Pierre-Simon de), riassumibile nell’affermazione che le leggi della fisica classica sono perfettamente deterministiche. È oggi ben chiaro che questa concezione non può essere più sostenuta per due diversi motivi: a) le leggi che regolano l’evoluzione del mondo fisico non sono esattamente deterministiche: infatti i fenomeni che avvengono su scala atomica sono governati dalla meccanica quantistica che è una teoria intrinsecamente probabilistica (➔ osservabile); b) anche in presenza di sistemi deterministici si può manifestare il fenomeno della forte sensibilità alle condizioni iniziali (➔ caos) che introduce una severa limitazione pratica alla possibilità di fare delle previsioni. Limitiamoci al problema della predizione in un ambito puramente deterministico: si vuole prevedere lo stato di un sistema, rappresentato matematicamente da un vettore x(t), conoscendo lo stato x(0) all’istante iniziale e la sua legge di evoluzione. Le più comuni leggi di evoluzione deterministiche sono le mappe e le equazioni differenziali; nel primo caso il tempo assume valori discreti e x(t) ha una legge di evoluzione del tipo
[1] formula
nel secondo caso il tempo è una variabile continua e la legge di evoluzione è del tipo
[2] formula
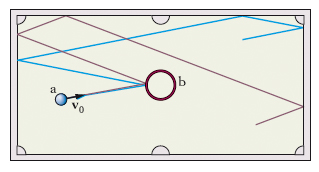
Per le mappe il determinismo è ben evidente: dato x(0) utilizzando la [1] si calcola x(1), iterando il procedimento si ottiene x(2), x(3), ..., fino a ottenere x(t). Per le equazioni differenziali il determinismo è una conseguenza del teorema, valido sotto ipotesi molto generali che sono in genere soddisfatte in equazioni differenziali di interesse fisico, di esistenza e unicità delle soluzioni. In pratica, la possibilità di p. a tempi lunghi è fortemente limitata da varie cause: a) non si ha mai una perfetta conoscenza dello stato iniziale x(0); b) nel calcolo numerico ci sono inevitabili errori introdotti dagli algoritmi di integrazione e dall’arrotondamento; c) la legge di evoluzione non è perfettamente nota. Un esempio è dato dalle previsioni meteorologiche. Questo problema è descritto da un sistema di equazioni differenziali alle derivate parziali, che vengono opportunamente approssimate per poter essere studiate al calcolatore. Anche nel caso, solo ipotetico, di poter disporre di un modello perfetto e di saper integrare le equazioni del moto senza errori (dovuti, per es., alla discretizzazione del problema e alla precisione finita del calcolatore) rimane sempre il problema delle condizioni iniziali. Lo stato dell’atmosfera a un dato istante non è certo noto con precisione molto alta, in quanto si dispone solo di un limitato numero di stazioni di rilevamento distribuite per di più in modo disomogeneo; gli strumenti di osservazione di ognuna di queste stazioni hanno inoltre un’accuratezza finita. In fig. è mostrato un altro tipico esempio di sistema a dipendenza sensibile dalle condizioni iniziali: la palla a si muove sul piano di un biliardo e urta elasticamente un ostacolo cilindrico fisso b e le sponde. Basta una minima differenza nella sola direzione della velocità iniziale v0 della palla per determinare due traiettorie molto diverse tra loro. Date due traiettorie x(t) e x′(t) ottenute a partire rispettivamente da x(0) e x′(0), in un sistema caotico si ha:
[3] formula
dove ε è ∣x(0)−x′(0)∣ e λ è l’esponente caratteristico di Ljapunov del sistema (➔). Se decidiamo di predire lo stato del sistema con una tolleranza δ sulla precisione della predizione, dalla [3] è possibile calcolare il tempo di p. Tp oltre il quale la previsione è affetta da un’imprecisione maggiore di δ:
[4] formula
In linea di principio Tp può essere esteso a piacere diminuendo ε, tuttavia, essendo logaritmica la dipendenza di Tp dal rapporto δ/ε, il tempo di p. è determinato essenzialmente da λ. Nei sistemi con una forte sensibilità alle condizioni iniziali dopo un tempo Tp∼c/λ (dove c dipende, ma poco, dallo sforzo impiegato nel determinare le condizioni iniziali) non ha più senso parlare di previsioni dello stato del sistema. Nel caso delle previsioni atmosferiche, per es., anche con un rilevamento da satellite dello stato iniziale, un modello matematico e algoritmi di integrazione molto accurati, non si potrà andare oltre un tempo ∼c/λ, dove λ è intrinseco alla dinamica dell’atmosfera mentre c dipende, solo logaritmicamente e quindi molto poco, dall’accuratezza del modello, dalla bontà dei dati iniziali e dalla precisione dell’integrazione numerica. Una stima sensata per 1/λ è dell’ordine di 10 giorni. La sensibile dipendenza dalle condizioni iniziali, fenomeno per il quale Eduard N. Lorenz coniò la locuzione ‘effetto farfalla’, può far sì che piccole incertezze su scale di qualche centimetro (provocate dal batter d’ali di una farfalla) si estendano amplificate su scale di qualche metro e così via fino a giungere alla scala di migliaia di kilometri in un paio di settimane.