servosistema
servosistema Sistema di comando o di controllo mediante il quale si ottiene che alcune grandezze (grandezze d’uscita, o grandezze asservite o controllate) seguano, secondo una certa legge, le variazioni delle grandezze di comando (o grandezze d’ingresso); in questo senso si differenzia dal caso dei sistemi di controllo adattativi per i quali eventuali variazioni delle condizioni operative del sistema si ripercuotono sulla grandezza di uscita (➔ regolazione).
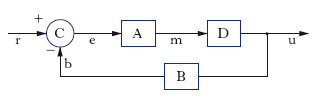
Schema di un sistema assevito
Il termine s., che in passato veniva utilizzato in luogo di o in alternativa ad asservimento, è sempre più spesso sostituito da sistema asservito. Lo schema è quello di fig. 1, in cui u ed e sono rispettivamente la grandezza controllata e quella applicata al dispositivo di controllo A, ottenuta, tramite il comparatore C, come differenza tra la grandezza di controreazione b e la grandezza di riferimento r. Il dispositivo di controllo A, che fornisce la grandezza di correzione m, comprende i regolatori e l’alimentatore per il sistema controllato D, mentre B è l’elemento di controreazione in cui sono incorporati possibili trasduttori. I s. sono in generale a controreazione e presentano caratteristiche peculiari, delle quali le più importanti sono: a) i s. spesso impiegano componenti dati a priori (elementi ‘fissi’), in quanto determinati in base a considerazioni ed esigenze diverse da quelle del controllo (per es., i servomotori con le loro caratteristiche commerciali, i processi e gli impianti da controllare ecc.); tali componenti devono essere accettati con le loro peculiarità, e gli unici elementi a disposizione del progettista sono gli elementi di correzione; b) nei s. sono presenti disturbi in punti anche diversi dall’ingresso (coppie resistenti, pressioni, temperature e in genere caratteristiche variabili dei sistemi controllati), ed è problema fondamentale minimizzarne gli effetti; c) gli elementi dei circuiti elettrici degli amplificatori sono piuttosto precisi e di caratteristiche invariabili per lunghi periodi di tempo; i componenti dei s. comprendono invece, oltre a quelli elettrici, elementi meccanici, idraulici, pneumatici, le cui caratteristiche sono determinabili con approssimazione di solito scarsa, ciò che rende la precisione dei s. inferiore a quella dei sistemi elettrici.
S. lineari e metodi di studio
I componenti elementari di un s. lineare devono essere tutti lineari; per essi le grandezze di uscita sono legate a quelle di entrata da relazioni esprimibili a mezzo di equazioni differenziali a coefficienti indipendenti dalle cause agenti. Per i s. lineari è valido il principio di sovrapposizione degli effetti; di conseguenza, variando l’ampiezza del comando senza modificarne la forma d’onda, la risposta muta d’ampiezza ma non muta di forma; è per questo che le prestazioni dei s. lineari si possono caratterizzare con le risposte a forme d’onda tipiche. Se i coefficienti che compaiono nelle equazioni di equilibrio non dipendono dal tempo, e indipendenti dal tempo sono quindi anche i parametri che caratterizzano tutti i componenti elementari del sistema, il s. si dice a parametri indipendenti dal tempo o normale. La stabilità di un s. lineare o la sua instabilità sono caratteristiche intrinseche, indipendenti dalle condizioni iniziali e dal modo in cui il sistema viene eccitato.
I metodi di studio dei s. lineari consistono in procedimenti di risoluzione delle equazioni differenziali lineari che definiscono il comportamento del s. o in tecniche particolari con cui si possono conoscere rapidamente, anche se in via approssimativa, le caratteristiche che interessano senza risolvere le equazioni stesse. La generalità, la semplicità e la completezza di tali metodi rendono ragione della grande diffusione dei s. lineari, che possono essere, per questo fatto, accuratamente progettati.
Assai utili sono i metodi basati sulla trasformata di Laplace, indirizzati allo scopo di ottenere, in modo rapido anche se approssimativo, informazioni sul comportamento del servosistema. Al rapporto fra le trasformate di Laplace della grandezza di uscita e di quella d’ingresso, il quale dipende unicamente dalle caratteristiche del sistema, si dà il nome di funzione di trasferimento del s.; essa è atta da sola a definirne completamente il funzionamento (sempre che il s. sia lineare e normale) e si riduce a una funzione reale razionale per i s. a costanti concentrate. La funzione di trasferimento di più s. lineari disposti in cascata è uguale al prodotto delle rispettive funzioni di trasferimento, purché i singoli sistemi non interagiscano fra loro. Nel caso di s. con controreazione, indicando con G(s) la funzione di trasferimento della catena d’azione e con H(s) quella della catena di controreazione, è chiamata funzione di trasferimento a catena aperta il loro prodotto, ovvero la funzione T(s)=G(s)•H(s); la funzione di trasferimento globale può essere scritta nella forma W(s)=G(s)/[1+T(s)].
Lo studio dei s. si effettua spesso sulla base della conoscenza della risposta in frequenza, cioè dell’andamento del guadagno complesso T(jν) in funzione della frequenza ν. In particolare è agevole, avvalendosi di tale metodo, soddisfare i requisiti richiesti per il s. quando essi si esprimano imponendo condizioni nel campo della frequenza; risulta altresì molto semplice e rapida la verifica della stabilità (➔). Per la descrizione della risposta in frequenza si utilizzano vari tipi di diagrammi. Oltre alla rappresentazione sul piano complesso si usano curve che rappresentano, in funzione della frequenza (o della pulsazione), rispettivamente il modulo (diagramma di attenuazione) e l’argomento (diagramma di fase) di T(jν).
Valutazione delle prestazioni di un s. lineare
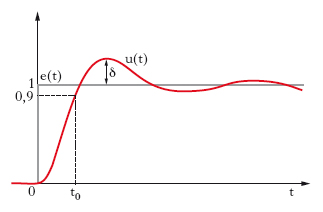
La fedeltà di un s. si può convenientemente valutare riferendosi al suo comportamento a comandi di forma d’onda tipica e, in particolare, rappresentabili con la funzione d’ingresso a gradino unitario (fig. 2). Si definiscono così: a) un errore a regime, caratterizzato dallo scarto fra uscita u(t) e ingresso e(t) dopo un tempo molto lungo dall’applicazione del comando; b) un errore transitorio, connesso con l’entità dello scarto tra uscita e ingresso nel periodo di tempo che precede lo stabilirsi del regime. Le caratteristiche di quest’ultimo si possono a loro volta convenzionalmente individuare a mezzo delle seguenti grandezze; c) tempo di salita, cioè il tempo t0 necessario per raggiungere una determinata frazione (per es., il 90%) del valore asintotico (di regime); d) tempo di assestamento, cioè il tempo X necessario perché l’ampiezza dell’oscillazione eventualmente presente scenda al disotto di una data frazione (per es., il 2%) del valore finale; e) valore percentuale della sovraelongazione δ, riferito al valore asintotico della risposta. Poiché la pendenza del fronte d’ingresso della risposta cresce all’aumentare della sovraelongazione, una buona precisione dinamica e una buona prontezza di risposta richiedono un valore non troppo piccolo della percentuale di sovraelongazione (per es., il 25%), che viene fissato in modo diverso a seconda delle applicazioni, e quindi un valore non eccessivamente ridotto di un ‘coefficiente di smorzamento’ da cui quello dipende, il quale caratterizza l’importanza relativa delle resistenze passive e degli elementi di natura reattiva. Un valore eccessivo della sovraelongazione è invece pericoloso perché può portare a instabilità.
La specificazione delle caratteristiche richieste può essere fatta riferendosi al campo delle frequenze anziché a quello temporale. Va tenuto presente che al crescere della larghezza di banda aumenta la fedeltà del s., ma peggiorano le sue proprietà filtranti, specie nei confronti del rumore; tale banda deve avere quindi la larghezza strettamente necessaria per ottenere le prestazioni desiderate, perché un suo ulteriore aumento può provocare una riduzione del rapporto segnale-rumore, e quindi, in definitiva, della precisione. Da questo punto di vista è in genere desiderabile una rapida caduta della curva di guadagno fuori della banda passante. La larghezza di banda varia in ragione inversa del tempo di salita. D’altro lato il rapporto fra le ampiezze della risposta e del comando, supposte entrambe funzioni sinusoidali del tempo, presenta in genere un (o più d’uno) massimo Mm per una (o più d’una) pulsazione ωm, che è detta pulsazione di risonanza. Al crescere di questa aumenta la larghezza di banda; l’aumento di Mm, a cui è legato il valore della sovraelongazione, diminuisce il margine di stabilità, mentre la sua diminuzione è dannosa per la prontezza.