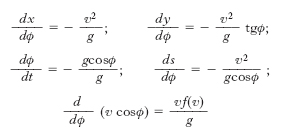balistica

Scienza che studia i problemi relativi al moto dei proietti lanciati da armi da fuoco, entro l’arma ( b. interna) e fuori di essa ( b. esterna). Nella b. si comprendono anche i problemi relativi al moto di razzi e di missili (➔ missile).

B. interna

Comprende la pirostatica (studio della combustione della polvere a volume costante) e la pirodinamica (studio della combustione della polvere a volume variabile entro la bocca da fuoco) e al suo sviluppo ha contribuito più la pratica sperimentale che non le ricerchge teoriche.

Pirostatica. - Per la pressione massima dei gas di combustione è stata trovata la formula empirica p = fd/(1−a d), in cui d è la densità di caricamento (cioè il rapporto tra la massa dell’esplosivo e il volume della camera di combustione), f una costante caratteristica detta ‘forza dell’esplosivo’, a il covolume specifico dei gas di combustione.

fig. 1

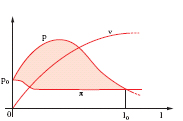
Pirodinamica. - La pressione del gas nella fase dinamica iniziale ha il valore dato dalla precedente relazione pirostatica; poi, una volta che il proietto, vinte le resistenze che si oppongono al suo moto, comincia ad avanzare, essa varia con legge diversa, aumentando fino a un valore massimo per poi decrescere; quando tutta la carica è bruciata, la pressione diminuisce secondo una legge che, data la rapidità del fenomeno, si può ritenere definita da una trasformazione adiabatica. Abitualmente si raccolgono in un unico grafico cartesiano (fig. 1) i diagrammi delle varie grandezze che si ha interesse di considerare nella b. interna, riportando sull’asse delle ascisse il percorso l del proietto lungo l’anima dell’arma, su quello delle ordinate, in opportune scale, la pressione p del gas che si sviluppa nell’esplosione della carica di lancio, la resistenza passiva specifica π, dovuta alla corona di forzamento, la velocità v del proietto. Il moto, accelerato, inizia quando la pressione p ha raggiunto un valore p_0, uguale al valore iniziale di π. L’area compresa tra l’asse delle ascisse, quello delle ordinate e il diagramma della pressione p, è proporzionale al lavoro totale; l’area compresa tra i diagrammi di p e di π (punteggiata in fig. 1) è invece proporzionale al lavoro utile. Il punto di incontro dei diagrammi di p e di π determina la lunghezza l₀ dell’arma. La pirodinamica fa capo, dal punto di vista analitico, a tre equazioni che permettono di studiare: la prima, il moto del proietto per azione dei gas prodotti dalla combustione; la seconda, il procedere della combustione della polvere nella bocca da fuoco; la terza, detta anche equazione fondamentale della pirodinamica, o equazione di Resal e Sarrau, il bilancio fra l’energia ottenibile dalla carica e quella sfruttata. In tali equazioni intervengono vari coefficienti di natura sperimentale.

B. esterna

fig. 2

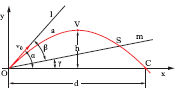
Dei problemi della b. esterna si sono occupati i maggiori matematici e fisici, da N. Tartaglia a G. Galilei, a I. Newton ecc. Elementi caratteristici del moto dei proietti sono (fig. 2): la traiettoria a; la linea di proiezione (o di tiro) l, semiretta della velocità iniziale v₀; l’angolo di proiezione α, che v₀ forma col piano orizzontale per O; il piano di tiro, piano verticale contenente la velocità iniziale (in fig., il piano Oxy); il punto di caduta C, in cui la traiettoria riattraversa il piano orizzontale per O; la gittata d, distanza tra bocca da fuoco O e punto di caduta C; la durata, tempo che il proietto impiega a passare da O in C; l’altezza del tiro, massima quota raggiunta dal proietto rispetto a Ox, cioè l’altezza h su Ox del vertice V della traiettoria; l’abbassamento del proietto, dislivello in valore assoluto, funzione dell’ascissa x, fra due punti giacenti rispettivamente sulla traiettoria e sulla linea di proiezione; l’abbassamento totale, quello corrispondente al punto di caduta. Si chiama poi linea di sito la semiretta m uscente da O e passante per il bersaglio S, angolo di elevazione (o di alzo) l’angolo β che OS forma con la linea di proiezione l e angolo di sito l’angolo γ che OS forma con l’orizzontale per O.

Moto dei proietti nel vuoto. - In prima e grossolana approssimazione, per i fini pratici, il moto dei proietti può essere studiato trascurando gli effetti dovuti alla rotazione terrestre e alla resistenza dell’aria. L’unica forza alla quale il proietto è soggetto è allora quella di gravità: in tal caso il moto è uniformemente accelerato, la traiettoria è una parabola ad asse verticale contenuta nel piano di tiro, volgente la concavità verso il basso e uscente dalla bocca da fuoco tangenzialmente alla velocità iniziale, di equazione:

fig. 3

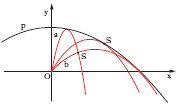
(g indica il valore dell’accelerazione di gravità). Assegnata v₀, si consideri (fig. 3) la parabola di sicurezza, inviluppo delle ∞¹ traiettorie paraboliche che si ottengono tenendo fissa la velocità iniziale v₀ e facendo variare l’angolo di proiezione α, cioè la parabola di equazione

se un bersaglio S è esterno alla parabola di sicurezza, non c’è nessuna traiettoria che vi passi ed esso non può essere raggiunto; se S è sulla parabola, vi è una sola traiettoria che passa per S; se è interno, ve ne sono due: se è il ramo ascendente che vi passa, si ha il tiro di lancio, se è il ramo discendente, il tiro arcato.

Moto dei proietti nell’aria. - I risultati che si ottengono trascurando la resistenza dell’aria (e la rotazione terrestre) sono, come si è detto, assai grossolani e inapplicabili in pratica alle moderne artiglierie; occorre inoltre tener conto della derivazione, deviazione laterale del proietto che è una conseguenza del moto di rotazione a esso impresso dalla rigatura dell’arma per la stabilizzazione del proietto stesso. Per la resistenza dell’aria l’esperienza suggerisce una espressione del tipo f (v) = ρ i F (v)/C, dove f è la resistenza riferita all’unità di massa, cioè l’accelerazione negativa che subisce il proietto (detta perciò ritardazione), ρ la densità dell’aria, i un coefficiente di forma del proietto, C il cosiddetto coefficiente balistico, uguale a m/(1000 A²), dove m è la massa in kg del proietto e A il diametro dello stesso in metri, F(v), funzione resistente, una funzione della sola velocità definita dal Siacci mediante la relazione:

Nell’ipotesi che la resistenza dell’aria sia opposta alla velocità, il moto risulta piano e le equazioni del moto si scrivono (P. Ballada di Saint-Robert):

nelle quali ϕ è l’angolo formato dal versore della tangente con l’asse x (inclinazione della traiettoria). L’ultima di queste prende nome di odografa e rappresenta la vera chiave di volta del problema balistico in quanto la sua integrazione permette di ridurre alle quadrature l’integrazione delle altre quattro. In generale l’integrazione esatta si sa eseguire solo per forme molto particolari della f(v), tra le quali quella indicata dal Bernoulli, f = a + bvⁿ, che per n = 2 si riduce al caso delle resistenze idrauliche (➔ resistenza). In ogni caso, dall’esame delle equazioni, si può ricavare un andamento qualitativo del moto e precisamente si vede che la traiettoria atmosferica, come quella parabolica, volge la concavità verso il basso lungo tutto il suo percorso e ha due archi: uno ascendente sino a un vertice in cui la tangente è orizzontale, e uno discendente; a differenza però della traiettoria parabolica, la traiettoria atmosferica presenta un asintoto verticale. Quanto all’integrazione dell’odografa, poiché le varie forme della resistenza corrispondono alla resistenza reale solo in casi particolari e per zone molto limitate del campo di variabilità della velocità, si è cercato di far ricorso a procedimenti approssimati, numerici o grafici, ovvero di alterare opportunamente la forma della resistenza. A.F. Siacci intuì che l’introduzione di una nuova variabile, funzione della velocità del proietto, può portare alla soluzione del problema. La nuova variabile u, legata alla velocità v dalla u = v cos ϕ/cos α, detta pseudovelocità, introdotta nelle equazioni del Saint-Robert, le rende integrabili. La soluzione dei problemi di b. esterna (particolarmente complessi quando si voglia tener conto anche delle dimensioni del proietto, del vento, ecc.) è oggi affidata a calcoli numerici eseguiti con elaboratori elettronici.